数形结合法:在数轴上表示的两个数,____________________.
 牛颦仵2022-10-04 11:39:541条回答
牛颦仵2022-10-04 11:39:541条回答
已提交,审核后显示!提交回复
共1条回复
 彩猪2000 共回答了12个问题
彩猪2000 共回答了12个问题 |采纳率75%- 右边的大于左边的,问的是这个吗?
- 1年前
相关推荐
- 高中数学问题用数形结合法求函数值域1.y=/x+1/+/x+4/ / /为绝对值2.y=根号下x方+4 +根号下x方+2
高中数学问题
用数形结合法求函数值域
1.y=/x+1/+/x+4/ / /为绝对值
2.y=根号下x方+4 +根号下x方+2x+10 的值域 阿炎电脑1年前2
阿炎电脑1年前2 -
 左珥 共回答了15个问题
左珥 共回答了15个问题 |采纳率93.3%答案
第一个;y=/x+1/+/x+4/;
可以看成y是x轴上一点到(-1,0)和(-4,0)点的距离的和;所以y>=3;
第二个;
可以看成y是点(x,0) 到点(0,2)点和点(-1,3)的距离的和;
所以y>=根号2;1年前查看全部
- 求函数值域问题利用换元法求函数y=sinxcosx+sinx+cosx的值域利用数形结合法1.求函数y=|x-1|+|2
求函数值域问题
利用换元法求函数y=sinxcosx+sinx+cosx的值域
利用数形结合法1.求函数y=|x-1|+|2x+1|的值域
2.求函数y=(1+sinx)/(2+cosx)的值域(2.如果用导数怎么求?) 百合子章1年前3
百合子章1年前3 -
 水蓝色- 共回答了23个问题
水蓝色- 共回答了23个问题 |采纳率91.3%1、利用换元法求函数y=sinxcosx+sinx+cosx的值域
令t=sinx+cosx
则sinxcosx=(t^2-((sinx)^2+(cosx)^2))/2
=(t^2-1)/2
y=sinxcosx+sinx+cosx
=(t^2-1)/2+t
=t^2/2+t-1/2
因为t=sinx+cosx=√2sin(x+π/4)
所以t的范围是【-√2,√2】
所以y=t^2/2+t-1/2的范围【-1,1/2+√2】
2、利用数形结合法求函数y=|x-1|+|2x+1|的值域
如图所示
①当x≥1时,y=x-1+2x+1=3x,
此时值域为【3,正无穷)
②当 -1/2<x<1时,y=1-x+2x+1=x+2
此时值域为(3/2,3)
③当x≤ -1/2,y=1-x-2x-1=-3x
此时值域为【3/2,正无穷)
3、用导数求函数y=(1+sinx)/(2+cosx)的值域
y ’ =((1+sinx)' *(2+cosx)-(1+sinx) *(2+cosx)')/(2+cosx)^2
=(sinx+2cosx+1)/(2+cosx)^2
=√5sin(x+φ)/(2+cosx)^2
令y‘ ≥0,求其递增区间
则√5sin(x+φ) ≥0
x∈【-φ+2πn,π-φ+2πn】
则递减区间为
x∈(π-φ+2πn,2π-φ+2πn)
所以y=(1+sinx)/(2+cosx)最大值在x=π-φ+2πn处
此时y=(1+sin(π-φ+2πn))/(2+cos(π-φ+2πn))
=(1-sinφ)/(2-cosφ)
前面可得sinφ=2√5/5,cosφ=√5/5
所以最大值y=(√5-2)/(2√5-1)
y=(1+sinx)/(2+cosx)最小值在x= -φ+2πn
代入可得y=(1-sinφ)/(2+cosφ)
=(√5-2)/(2√5+1)
所以导数的范围【(√5-2)/(2√5+1),(√5-2)/(2√5-1)】
这题答案未能分母有理化如果有需要的话化一下也快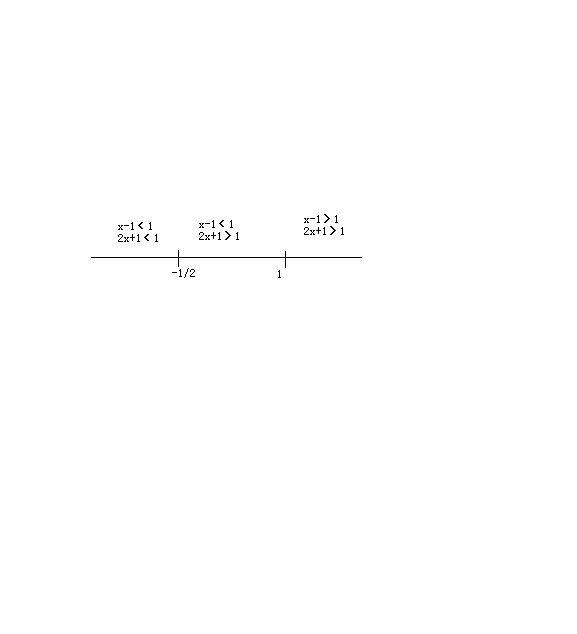 1年前查看全部
1年前查看全部
- .什么是待定系数法,数形结合法,整体代入法
 interlong321年前1
interlong321年前1 -
 axtswy 共回答了14个问题
axtswy 共回答了14个问题 |采纳率85.7%待定系数法,一种求未知数的方法.将一个多项式表示成另一种含有待定系数的新的形式,这样就得到一个恒等式.然后根据恒等式的性质得出系数应满足的方程或方程组,其后通过解方程或方程组便可求出待定的系数,或找出某些系数所满足的关系式,这种解决问题的方法叫做待定系数法.
数与形是数学中的两个最古老,也是最基本的研究对象,它们在一定条件下可以相互转化.
中学数学研究的对象可分为两大部分,一部分是数,一部分是形,但数与形是有联系的,这个联系称之为数形结合,或形数结合.我国著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事非.“数”与“形”反映了事物两个方面的属性.我们认为,数形结合,主要指的是数与形之间的一一对应关系.数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过“以形助数”或“以数解形”即通过抽象思维与形象思维的结合,可以使复杂问题简单化,抽象问题具体化,从而起到优化解题途径的目的.
作为一种数学思想方法,数形结合的应用大致又可分为两种情形:或者借助于数的精确性来阐明形的某些属性,或者借助形的几何直观性来阐明数之间某种关系,即数形结合包括两个方面:第一种情形是“以数解形”,而第二种情形是“以形助数”.“以数解形”就是有些图形太过于简单,直接观察却看不出什么规律来,这时就需要给图形赋值,如边长、角度等等.
整体与部分的辩证.只有相对于部分所构成的整体而言,才是一个确定的部分,没有整体,也无所谓部分.部分作为整体的组成,有时也可以当作一个整体.在数学上,从问题的整体性质出发,突出对问题的整体结构的分析和改造,发现问题的整体结构特征,善于用“集成”的眼光,把某些式子或图形看成一个整体,把握它们之间的关联,进行有目的的、有意识的整体处理.所谓善于用“集成”的思想,譬如,航天飞机有无数多的元器件组成,某个元器件发生故障,把该元器件所在的集成板整体换掉1年前查看全部
- 函数y=lg(x^2-2mx+m+2)的值域是R,则为什么delta>=0用数形结合法来给我解析一下!
 yca55626781年前2
yca55626781年前2 -
 xy_xia 共回答了19个问题
xy_xia 共回答了19个问题 |采纳率94.7%值域是R说明x^2-2mx+m+2必然 有零点 (如果 x^2-2mx+m+2恒大于 0,例如 恒大于正实数 r,则 y的值域必然是 y>lgr)
既然有解 ,那么 delta自然大于等于 0
我不知道数型结合如何解释这个1年前查看全部
- 一元二次的根:整数根一元二次方程的特殊解法---参数法,构造法,数形结合法,反证法,分类讨论法怎么做.还有一元二次方程的
一元二次的根:整数根
一元二次方程的特殊解法---参数法,构造法,数形结合法,反证法,分类讨论法怎么做.还有一元二次方程的根中的特殊根:有理数根 ,整数根,素数根,奇偶数根怎么求.什么是素数根? 吴人飞飞1年前2
吴人飞飞1年前2 -
 秦岭汉水 共回答了13个问题
秦岭汉水 共回答了13个问题 |采纳率92.3%一元二次方程的解法
一、知识要点:
一元二次方程和一元一次方程都是整式方程,它是初中数学的一个重点内容,也是今后学习数学的基
础,应引起同学们的重视.
一元二次方程的一般形式为:ax2+bx+c=0, (a≠0),它是只含一个未知数,并且未知数的最高次数是2
的整式方程.
解一元二次方程的基本思想方法是通过“降次”将它化为两个一元一次方程.一元二次方程有四种解
法:1、直接开平方法;2、配方法;3、公式法;4、因式分解法.
二、方法、例题精讲:
1、直接开平方法:
直接开平方法就是用直接开平方求解一元二次方程的方法.用直接开平方法解形如(x-m)2=n (n≥0)的
方程,其解为x=m± .
例1.解方程(1)(3x+1)2=7 (2)9x2-24x+16=11
分析:(1)此方程显然用直接开平方法好做,(2)方程左边是完全平方式(3x-4)2,右边=11>0,所以
此方程也可用直接开平方法解.
(1)(3x+1)2=7×
∴(3x+1)2=5
∴3x+1=±(注意不要丢解)
∴x=
∴原方程的解为x1=,x2=
(2) 9x2-24x+16=11
∴(3x-4)2=11
∴3x-4=±
∴x=
∴原方程的解为x1=,x2=
2.配方法:用配方法解方程ax2+bx+c=0 (a≠0)
先将常数c移到方程右边:ax2+bx=-c
将二次项系数化为1:x2+x=-
方程两边分别加上一次项系数的一半的平方:x2+x+( )2=- +( )2
方程左边成为一个完全平方式:(x+ )2=
当b2-4ac≥0时,x+ =±
∴x=(这就是求根公式)
例2.用配方法解方程 3x2-4x-2=0
将常数项移到方程右边 3x2-4x=2
将二次项系数化为1:x2-x=
方程两边都加上一次项系数一半的平方:x2-x+( )2= +( )2
配方:(x-)2=
直接开平方得:x-=±
∴x=
∴原方程的解为x1=,x2= .
3.公式法:把一元二次方程化成一般形式,然后计算判别式△=b2-4ac的值,当b2-4ac≥0时,把各项
系数a, b, c的值代入求根公式x=(b2-4ac≥0)就可得到方程的根.
例3.用公式法解方程 2x2-8x=-5
将方程化为一般形式:2x2-8x+5=0
∴a=2, b=-8, c=5
b2-4ac=(-8)2-4×2×5=64-40=24>0
∴x= = =
∴原方程的解为x1=,x2= .
4.因式分解法:把方程变形为一边是零,把另一边的二次三项式分解成两个一次因式的积的形式,让
两个一次因式分别等于零,得到两个一元一次方程,解这两个一元一次方程所得到的根,就是原方程的两个
根.这种解一元二次方程的方法叫做因式分解法.
例4.用因式分解法解下列方程:
(1) (x+3)(x-6)=-8 (2) 2x2+3x=0
(3) 6x2+5x-50=0 (选学) (4)x2-2( + )x+4=0 (选学)
(1)(x+3)(x-6)=-8 化简整理得
x2-3x-10=0 (方程左边为二次三项式,右边为零)
(x-5)(x+2)=0 (方程左边分解因式)
∴x-5=0或x+2=0 (转化成两个一元一次方程)
∴x1=5,x2=-2是原方程的解.
(2)2x2+3x=0
x(2x+3)=0 (用提公因式法将方程左边分解因式)
∴x=0或2x+3=0 (转化成两个一元一次方程)
∴x1=0,x2=-是原方程的解.
注意:有些同学做这种题目时容易丢掉x=0这个解,应记住一元二次方程有两个解.
(3)6x2+5x-50=0
(2x-5)(3x+10)=0 (十字相乘分解因式时要特别注意符号不要出错)
∴2x-5=0或3x+10=0
∴x1=, x2=- 是原方程的解.
(4)x2-2(+ )x+4 =0 (∵4 可分解为2 ·2 ,∴此题可用因式分解法)
(x-2)(x-2 )=0
∴x1=2 ,x2=2是原方程的解.
小结:
一般解一元二次方程,最常用的方法还是因式分解法,在应用因式分解法时,一般要先将方程写成一般
形式,同时应使二次项系数化为正数.
直接开平方法是最基本的方法.
公式法和配方法是最重要的方法.公式法适用于任何一元二次方程(有人称之为万能法),在使用公式
法时,一定要把原方程化成一般形式,以便确定系数,而且在用公式前应先计算判别式的值,以便判断方程
是否有解.
配方法是推导公式的工具,掌握公式法后就可以直接用公式法解一元二次方程了,所以一般不用配方法
解一元二次方程.但是,配方法在学习其他数学知识时有广泛的应用,是初中要求掌握的三种重要的数学方
法之一,一定要掌握好.(三种重要的数学方法:换元法,配方法,待定系数法).
例5.用适当的方法解下列方程.(选学)
(1)4(x+2)2-9(x-3)2=0 (2)x2+(2-)x+ -3=0
(3) x2-2 x=- (4)4x2-4mx-10x+m2+5m+6=0
分析:(1)首先应观察题目有无特点,不要盲目地先做乘法运算.观察后发现,方程左边可用平方差
公式分解因式,化成两个一次因式的乘积.
(2)可用十字相乘法将方程左边因式分解.
(3)化成一般形式后利用公式法解.
(4)把方程变形为 4x2-2(2m+5)x+(m+2)(m+3)=0,然后可利用十字相乘法因式分解.
(1)4(x+2)2-9(x-3)2=0
[2(x+2)+3(x-3)][2(x+2)-3(x-3)]=0
(5x-5)(-x+13)=0
5x-5=0或-x+13=0
∴x1=1,x2=13
(2) x2+(2- )x+ -3=0
[x-(-3)](x-1)=0
x-(-3)=0或x-1=0
∴x1=-3,x2=1
(3)x2-2 x=-
x2-2 x+ =0 (先化成一般形式)
△=(-2 )2-4 ×=12-8=4>0
∴x=
∴x1=,x2=
(4)4x2-4mx-10x+m2+5m+6=0
4x2-2(2m+5)x+(m+2)(m+3)=0
[2x-(m+2)][2x-(m+3)]=0
2x-(m+2)=0或2x-(m+3)=0
∴x1= ,x2=
例6.求方程3(x+1)2+5(x+1)(x-4)+2(x-4)2=0的二根. (选学)
分析:此方程如果先做乘方,乘法,合并同类项化成一般形式后再做将会比较繁琐,仔细观察题目,我
们发现如果把x+1和x-4分别看作一个整体,则方程左边可用十字相乘法分解因式(实际上是运用换元的方
法)
[3(x+1)+2(x-4)][(x+1)+(x-4)]=0
即 (5x-5)(2x-3)=0
∴5(x-1)(2x-3)=0
(x-1)(2x-3)=0
∴x-1=0或2x-3=0
∴x1=1,x2=是原方程的解.
例7.用配方法解关于x的一元二次方程x2+px+q=0
x2+px+q=0可变形为
x2+px=-q (常数项移到方程右边)
x2+px+( )2=-q+()2 (方程两边都加上一次项系数一半的平方)
(x+)2= (配方)
当p2-4q≥0时,≥0(必须对p2-4q进行分类讨论)
∴x=- ±=
∴x1= ,x2=
当p2-4q1年前查看全部
大家在问
- 1六年级师生共360人,准备去秋游,到汽车出租公司得到这样的信息:
- 2如果,你是湖水,我乐意堤岸环绕.句子仿写,
- 3海上有鸟是不是就离陆地不远
- 4现在的老师为什么不是人,英语的作业都还多,变态.
- 5已知m的2次方+m-1=0,试求代数式m的3次方+2m的2次方+2011的值.
- 6互为相反数的两个数,在数轴上两点间的距离为11,你能求出这两个数吗?你能在数轴上找出两个互为相反数间的距离最小的数吗?
- 7如图,在平面直角坐标系中,△ABC的边BC平行x轴,三顶点坐标分别为A(-x+2y,x+y)、B(-x-y,2y)、C(
- 8用英语翻译你表妹看起来像啥样?
- 9我的妹妹正在看书,译成英文
- 10你的 妹妹叫什么 译成英文
- 11“胜日寻芳泗水滨”的下半句是?
- 12x^2(x-1)^2+(1-k^2)(x-1)^2+2x=0的实数解个数
- 13如果你是湖水,我乐意堤岸环绕. 山岭我 乐意装点姿容的青草这句小诗是当代诗人谁写的?
- 14英语翻译“如果有天我归去,你会不会比那些年更爱我?我想我会”翻译成英语,求修改下面这句If one day I went
- 1525分之150约分
