点p（x1,y1）在圆x2+y2=r2内,则直线x1x+y1y=r2与已知圆的公共点的个数

hjsbxer2022-10-04 11:39:541条回答

已提交，审核后显示！提交回复

共1条回复

瓢虫二一只共回答了22个问题 | 采纳率81.8%: 圆心O(0,0)
P在圆内
所以PO小于半径
即√(x1²+y1²)1
r²/√(x1²+y1²)>r
圆心到直线距离=|0+0-r²|/√(x1²+y1²)
=r²/√(x1²+y1²)>r
即圆心到直线距离大于半径,相离
所以公共点个数是0; 1年前

相关推荐

已知点P（a，b）在圆x2+y2=r2的内部，则直线ax+by=r2与圆的位置关系（　　） 已知点P（a，b）在圆x²+y²=r²的内部，则直线ax+by=r²与圆的位置关系（　　） A. 相交 B. 相离 C. 相切 D. 不能确定 蓝梦冰橙1年前0: 共回答了个问题 | 采纳率

查看全部

已知点M（a，b）（ab≠0）是圆x2+y2=r2内一点，直线g是以M为中点的弦所在直线，直线l的方程为ax+by+r2 已知点M（a，b）（ab≠0）是圆x²+y²=r²内一点，直线g是以M为中点的弦所在直线，直线l的方程为ax+by+r²=0，则直线l（　　） A．l∥g，且与圆相切 B．l∥g，且与圆相离 C．l⊥g，且与圆相切 D．l⊥g，且与圆相离 basbascat1年前1: 止损共回答了19个问题 | 采纳率94.7%

解题思路：由条件求得直线l的斜率，再求出直线m的斜率，可得它们的斜率相等．利用点到直线的距离公式求得圆心C到直线m的距离大于半径，由此可得l∥m且m与圆c相离．
由题意可得a²+b²＜r²，设圆心为C，且CM⊥直线g，故直线g的斜率为-[1
kCM=-
a/b]，
由于直线l的方程为ax+by+r²=0，则l的斜率为-[a/b]，
圆心C到直线l的距离等于
|0+0+r2|

a2+b2＞r，
故l∥g且l与圆c相离，
故选B．

点评：
本题考点：轨迹方程．

考点点评：本题主要考查直线和圆的位置关系，点到直线的距离公式的应用，属于中档题．

1年前查看全部

有如下结论：“圆x2+y2=r2上一点P（x0，y0）处的切线方程为x0y+y0y=r2”，类比也有结论：“椭圆x2a2 有如下结论：“圆x²+y²=r²上一点P（x₀，y₀）处的切线方程为x₀y+y₀y=r²”，类比也有结论：“椭圆 x2 a2 + y2 b2 =1（a＞b＞0）上一点P（x₀，y₀）处的切线方程为 x0x a2 + y0y b2 =1”，过椭圆C： x2 2 +y2＝1的右准线l上任意一点M引椭圆C的两条切线，切点为 A、B．直线AB恒过一定点______． sssunshine1年前1: hat122 共回答了12个问题 | 采纳率91.7%

解题思路：设出M的坐标，及两个切点的坐标，由椭圆方程写出切线方程，把M的坐标代入切线方程，得到切点所在的直线方程，即可得到结论．
设M（2，t）（t∈R），A（x₁，y₁），B（x₂，y₂），则MA的方程为
x1x
2+y1y＝1
∵点M在MA上，∴x₁+ty₁=1①，同理可得x₂+ty₂=1 ②
由①②知AB的方程为 x+ty=1，即x-1=ty
∴直线AB恒过一定点（1，0）
故答案为（1，0）

点评：
本题考点：类比推理．

考点点评：本题考查类比推理，考查椭圆的切线方程，考查直线恒过定点，属于基础题．

1年前查看全部

已知圆的方程式x2+y2=r2，经过圆上一点M（x0，y0）的切线方程为x0x+y0y=r2，类别上述方法可以得到椭圆x 已知圆的方程式x²+y²=r²，经过圆上一点M（x₀，y₀）的切线方程为x₀x+y₀y=r2，类别上述方法可以得到椭圆 x2 a2 + y2 b2 ＝1类似的性质为：经过椭圆上一点M（x₀，y₀）的切线方程为 x0x a2 + y0y b2 ＝1 x0x a2 + y0y b2 ＝1 ． 小竹5231年前1: czhongqing 共回答了16个问题 | 采纳率87.5%

解题思路：由过圆x²+y²=r²上一点的切线方程x₀x+y₀y=r²，我们不难类比推断出过椭圆上一点的切线方程：用x₀x代x²，用y₀y代y²，即可得．
类比过圆上一点的切线方程，可合情推理：
过椭圆
x2
a2+
y2
b2＝1（a＞b＞0），上一点P（x₀，y₀）处的切线方程为

x0
a2x+
y0
b2y＝1．
故答案为：
x0x
a2+
y0y
b2＝1．

点评：
本题考点：椭圆的应用；类比推理．

考点点评：本题考查椭圆的应用、利用类比推理得到结论、证明类比结论时证明过程与其类比对象的证明过程类似或直接转化为类比对象的结论．

1年前查看全部

已知点A（-5，0），B（-1，-3），若圆x2+y2=r2（r＞0）上恰有两点M，N，使得△MAB和△NAB的面积均为 已知点A（-5，0），B（-1，-3），若圆x²+y²=r²（r＞0）上恰有两点M，N，使得△MAB和△NAB的面积均为5，则r的取值范围是______． qindalang1年前1: 没事干怎么办共回答了11个问题 | 采纳率81.8%

解题思路：先求得|AB|=5，根据题意可得两点M，N到直线AB的距离为2．求出AB的方程为3x+4y+15=0，当圆上只有一个点到直线AB的距离为2 时，求得r的值；当圆上只有3个点到直线AB的距离为2时，求得r的值，从而求得满足条件的r的取值范围．
由题意可得|AB|=
(-1+5)2+(-3-0)2=5，根据△MAB和△NAB的面积均为5，
可得两点M，N到直线AB的距离为2．
由于AB的方程为 [y-0/-3-0]=[x+5/-1+5]，即 3x+4y+15=0．
若圆上只有一个点到直线AB的距离为2，
则有圆心（0，0）到直线AB的距离
|0+0+15|

9+16=r+2，解得r=1．
若圆上只有3个点到直线AB的距离为2，
则有圆心（0，0）到直线AB的距离
|0+0+15|

9+16=r-2，解得r=5，
故答案为：（1，5）．

点评：
本题考点：直线与圆的位置关系．

考点点评：本题主要考查直线和圆的位置关系，点到直线的距离公式的应用，属于基础题．

1年前查看全部

已知A、B、C是圆O：x2+y2=r2上三点，且OA+OB＝OC，则AB•OC等于（　　） 已知A、B、C是圆O：x²+y²=r²上三点，且 OA + OB ＝ OC ，则 AB • OC 等于（　　） A．0 B．[1/2] C．[3/2] D．-[3/2] 风之爱1年前1

ammy1224 共回答了16个问题 | 采纳率93.8%

解题思路：由A、B、C是圆O：x²+y²=r²上三点，

＝

，知

⊥

，由此能求出

•

=0．

∵A、B、C是圆O：x²+y²=r²上三点，

OA+

OB＝

OC，
∴

AB⊥

OC，
∴

AB•

OC=0．
故选A．

点评：
本题考点：向量加减混合运算及其几何意义；圆的标准方程．

考点点评：本题考查向量的加减运算及其几何意义，是基础题．解题时要认真审题，仔细解答，注意合理地进行等价转化．

1年前查看全部

若圆x2+y2=r2（r＞0）上仅有4个点到直线x-y-2=0的距离为1，则实数r的取值范围（　　） 若圆x²+y²=r²（r＞0）上仅有4个点到直线x-y-2=0的距离为1，则实数r的取值范围（　　） A. .r＞ 2 +1 B. 2 −1＜r＜ 2 +1 C. 0＜r＜ 2 −1 D. 0＜r＜ 2 +1 find慧1年前1

3510518 共回答了24个问题 | 采纳率100%

解题思路：求出圆心到直线x-y-2=0的距离为

|0−0−2|

，依据题意，直线和圆相交，在直线的两侧，圆上各有两个点到直线的距离等于1，r-

＞1，故半径r应大于

+1．

圆x²+y²=r²（r＞0）的圆心到直线x-y-2=0的距离为
|0−0−2|

2=
2，
故半径应大于
2+1，
故选A．

点评：
本题考点：直线与圆相交的性质．

考点点评：本题考查直线和圆的位置关系，点到直线的距离公式的应用，体现了转化的数学思想．

1年前查看全部

已知圆C：x2+y2=r2（r＞0）经过点（1，3）． 已知圆C：x²+y²=r²（r＞0）经过点（1， 3 ）． （1）求圆C的方程； （2）是否存在经过点（-1，1）的直线l，它与圆C相交于A，B两个不同点，且满足 OM =[1/2] OA + 3 2 OB （O为坐标原点）关系的点M也在圆C上？如果存在，求出直线l的方程；如果不存在，请说明理由． 决不还债11年前0: 共回答了个问题 | 采纳率

查看全部

在平面直角坐标系xOy中，直线l：x-y+3=0与圆O：x2+y2=r2（r＞0）相交于A，B两点．若OA+2OB=3O 在平面直角坐标系xOy中，直线l：x-y+3=0与圆O：x²+y²=r²（r＞0）相交于A，B两点．若 OA +2 OB = 3 OC ，且点C也在圆O上，则圆O的方程为______． 朝贝夕拾1年前1: viven95 共回答了17个问题 | 采纳率82.4%

解题思路：联立直线与圆的方程即可得到根与系数的关系，再利用已知向量关系式，即可得出点C的坐标满足的关系式，代入圆的方程又得出点A，B的坐标的关系式，联立即可解出．
设点A（x₁，y₁），B（x₂，y₂）．
联立

x−y+3＝0
x2+y2＝r2，消去y得到关于x的一元二次方程2x²+6x+9-r²=0，
∵直线l与圆O相较于A、B两点，则△=36-8（9-r²）＞0．（*）
∴x₁+x₂=-3，x1x2＝
9−r2
2．
设点C（x₀，y₀）．
∵

OA+2

OB=
3

OC，∴(x1，y1)+2(x2，y2)＝
3(x0，y0)，
又∵y₁=x₁+3，y₂=x₂+3．
∴可得：

点评：
本题考点：向量在几何中的应用；直线与圆相交的性质．

考点点评：熟练掌握直线与圆相交问题变得解题模式、根与系数的关系、向量相等、方程对的思想方法是解题的关键．

1年前查看全部

点P（x0，y0）在圆x2+y2=r2内，则直线x0x+y0y＝r2和已知圆的公共点的个数为（　　） 点P（x₀，y₀）在圆x²+y²=r²内，则直线x0x+y0y＝r2和已知圆的公共点的个数为（　　） A. 0 B. 1 C. 2 D. 不能确定 西瓜霜10001年前1: fatjohn 共回答了15个问题 | 采纳率86.7%

解题思路：先利用点到直线的距离，求得圆心到直线x₀x+y₀y=r²的距离，根据P在圆内，判断出 x₀²+y₀²＜r²，进而可知d＞r，故可知直线和圆相离．
圆心O（0，0）到直线x₀x+y₀y=r²的距离为d=
r2

x20+
y20
∵点M（x₀，y₀）在圆内，∴x₀²+y₀²＜r²，则有d＞r，
故直线和圆相离，直线与圆的公共点为0个
故选A．

点评：
本题考点：点与圆的位置关系．

考点点评：本题主要考查了直线与圆的位置关系．考查了数形结合的思想，直线与圆的位置关系的判定．解题的关键是看圆心到直线的距离与圆的半径的大小关系．

1年前查看全部

点A是圆上O：x2+y2=r2(r大于0)上任意一点,AB垂直X轴,垂足为B,以A为圆心,|AB|为半径的圆交圆O于C, 点A是圆上O：x2+y2=r2(r大于0)上任意一点,AB垂直X轴,垂足为B,以A为圆心,|AB|为半径的圆交圆O于C,D两点,连接CD交AB与点M,当点A在圆上运动时,求点M的轨迹方程. WIWBB1年前2: dongmian_2 共回答了18个问题 | 采纳率94.4%

A(a,b)
B(a,0)
所以圆A(x-a)^2+(y-b)^2=b^2
x^2+y^2-2ax-2by+a^2=0
x^2+y^2=r^2
相减
2ax+2by-a^2=r^2
这就是CD所在直线
AB是x=a
所M横坐标是a
2a^2+2by-a^2=r^2
y=(r^2-a^2)/2b
A在圆上
a^2+b^2=r^2
r^2-a^2=b^2
y=b^2/2b=b/2,b=2y
x=a
a^2+b^2=r^2
所以x^2+4y^2=r^2

1年前查看全部

已知圆 c:x2+y2=r2（r＞0）和点p(a.b) 若点P在C上求过点P且与 已知圆 c:x2+y2=r2（r＞0）和点p(a.b) 若点P在C上求过点P且与 C相切的直线方程 也摸鱼儿1年前1: fgfgdddd 共回答了16个问题 | 采纳率81.3%

设直线上任意不同于P的一点为Q（x,y）,因为直线与圆相切,故有PQ向量垂直OP向量（设原点为O）,PQ向量=（x-a,y-b）,OP向量=（a,b）,所以a（x-a）+b（y-b）=0,即ax+by=a2+b2,因为P在圆C上,所以a2+b2=r2,所以ax+by=r2,故直线方程为ax+by=r2.

1年前查看全部

点P（x0，y0）在圆x2+y2=r2内，则直线x0x+y0y＝r2和已知圆的公共点的个数为（　　） 点P（x₀，y₀）在圆x²+y²=r²内，则直线x0x+y0y＝r2和已知圆的公共点的个数为（　　） A. 0 B. 1 C. 2 D. 不能确定 颓废壮汉1年前1: leonmoon 共回答了18个问题 | 采纳率100%

解题思路：先利用点到直线的距离，求得圆心到直线x₀x+y₀y=r²的距离，根据P在圆内，判断出 x₀²+y₀²＜r²，进而可知d＞r，故可知直线和圆相离．
圆心O（0，0）到直线x₀x+y₀y=r²的距离为d=
r2

x20+
y20
∵点M（x₀，y₀）在圆内，∴x₀²+y₀²＜r²，则有d＞r，
故直线和圆相离，直线与圆的公共点为0个
故选A．

点评：
本题考点：点与圆的位置关系．

考点点评：本题主要考查了直线与圆的位置关系．考查了数形结合的思想，直线与圆的位置关系的判定．解题的关键是看圆心到直线的距离与圆的半径的大小关系．

1年前查看全部

（2013•南通二模）在平面直角坐标系xOy中，已知圆C：x2+y2=r2和直线l：x=a（其中r和a均为常数，且0＜r （2013•南通二模）在平面直角坐标系xOy中，已知圆C：x²+y²=r²和直线l：x=a（其中r和a均为常数，且0＜r＜a），M为l上一动点，A₁，A₂为圆C与x轴的两个交点，直线MA₁，MA₂与圆C的另一个交点分别为P、Q． （1）若r=2，M点的坐标为（4，2），求直线PQ方程； （2）求证：直线PQ过定点，并求定点的坐标． 667w6hd1年前1: duoduo502 共回答了17个问题 | 采纳率100%

解题思路：（1）通过r=2，M点的坐标为（4，2），求出A₁（-2，0），A₂（2，0）．然后推出P、Q坐标，即可求直线PQ方程；
（2）证明法一：设A₁（-r，0），A₂（r，0）．设M（a，t），求出直线MA₁的方程，直线MA₁的方程，通过直线与圆的方程联立，求出直线PQ的方程，然后说明经过定点，求定点的坐标．
法二：设得A₁（-r，0），A₂（r，0）．设M（a，t），求出直线MA₁的方程，与圆C的交点P设为P（x₁，y₁）．求出直线MA₂的方程，与圆C的交点Q设为Q（x₂，y₂）．点P（x₁，y₁），Q（x₂，y₂）在曲线[（a+r）y-t（x+r）][（a-r）y-t（x-r）]=0上，有P（x₁，y₁），Q（x₂，y₂）在圆C上，求出公共弦方程，说明经过定点，求定点的坐标．
（1）当r=2，M（4，2），则A₁（-2，0），A₂（2，0）．
直线MA₁的方程：x-3y+2=0，解

x2+y2＝4
x−3y+2＝0得P(
8
5，
6
5)．…（2分）
直线MA₂的方程：x-y-2=0，解

x2+y2＝4
x−y−2＝0得Q（0，-2）． …（4分）
由两点式，得直线PQ方程为：2x-y-2=0． …（6分）
（2）证法一：由题设得A₁（-r，0），A₂（r，0）．设M（a，t），
直线MA₁的方程是：y=[t/a+r]（x+r），
直线MA₁的方程是：y=[t/a−r]（x-r）．…（8分）
解

x2+y2＝r2
y＝
t
a+r(x+r)得P(
r(a+r)

点评：
本题考点：直线与圆的位置关系；恒过定点的直线．

考点点评：不考查直线与圆的位置关系，直线系方程的应用，考查计算能力与转化思想．

1年前查看全部

在平面直角坐标系xOy中，直线l：x-y+3=0与圆O：x2+y2=r2（r＞0）相交于A，B两点．若OA+2OB=3O 在平面直角坐标系xOy中，直线l：x-y+3=0与圆O：x²+y²=r²（r＞0）相交于A，B两点．若 OA +2 OB = 3 OC ，且点C也在圆O上，则圆O的半径r= 3 2 3 2 ． 铥铥灬奶糖1年前1: 爱上渡边君共回答了27个问题 | 采纳率96.3%

设点A（x₁，y₁），B（x₂，y₂）．
联立x-y+3=0与圆O：x²+y²=r²（r＞0）
，消去y得到关于x的一元二次方程2x²+6x+9-r²=0，
∵直线l与圆O相较于A、B两点，则△=36-8（9-r²）＞0．（*）
∴x₁+x₂=-3，x₁•x₂=
9−r2
2．
设点C（x₀，y₀）．
∵

OA+2

OB=
3

OC，且点C也在圆O上，
（x₁，y₁，）+2（x₂，y₂）=
3（x₀，y₀）．
又∵y₁=x₁+3，y₂=x₂+3．
∴可得：

x0＝
x1+2x2

1年前查看全部

（2012•广州一模）已知点P（a，b）（ab≠0）是圆O：x2+y2=r2内一点，直线l的方程为ax+by+r2=0， （2012•广州一模）已知点P（a，b）（ab≠0）是圆O：x²+y²=r²内一点，直线l的方程为ax+by+r²=0，那么直线l与圆O的位置关系是（　　） A．相离 B．相切 C．相交 D．不确定 flyingzerg_20061年前1

wangzi2006105406 共回答了24个问题 | 采纳率87.5%

解题思路：由题意可得

a2+b 2

＜半径r，求出圆心（0，0）到直线的距离大于半径，可得直线和圆相离，从而得到答案．

∵点P（a，b）（ab≠0）是圆O：x²+y²=r²内一点，∴
a2+b 2＜半径r．
圆心（0，0）到直线ax+by+r²=0的距离等于
|0+0+r 2|

a2+b 2＞
r2
r=r，
故直线和圆相离，
故选A．

点评：
本题考点：直线与圆的位置关系．

考点点评：本题主要考查直线和圆的位置关系，点到直线的距离公式的应用，属于中档题．

1年前查看全部

已知椭圆C1：x2a2+y2b2=1（a＞b＞0）和圆C2：x2+y2=r2（r＞0）都过点P（-1，0），且椭圆C1离 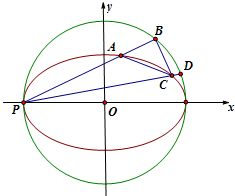已知椭圆C₁： x2 a2 + y2 b2 =1（a＞b＞0）和圆C₂：x²+y²=r²（r＞0）都过点P（-1，0），且椭圆C₁离心率为 2 2 ，过点P作斜率为k₁，k₂的直线分别交椭圆C₁、圆C₂于点A、B、C、D（如图），k₁=2k₂． （1）求椭圆C₁和圆C₂的方程； （2）求证：直线BC恒过定点． 菜_霸1年前1: frizzleyf 共回答了21个问题 | 采纳率90.5%

解题思路：（1）直接把定点代入圆的方程求圆的半径，利用椭圆过定点得到a的值，代入离心率后求得c的值，结合b²=a²-c²求得b的值，则圆与椭圆的方程可求；
（2）设出直线AB和CD的方程，分别和圆与椭圆联立后求出A，B，C，D的坐标，求出BC的斜率（用k₂）表示，由点斜式写出直线BC的方程后可得直线BC恒过定点．
（1）由圆C₂：x²+y²=r²（r＞0）过点P（-1，0），得到r²=1，
所以圆C₂的方程为x²+y²=1．
由椭圆C₁离心率为e＝
c
a=

2
2，
由椭圆C₁：
x2
a2+
y2
b2=1（a＞b＞0）过点P（-1，0），得[1
a2＝1，
所以a=1，代入
c/a＝

2
2]，得c=

2
2，
所以b2＝a2−c2＝
1
2．
所以椭圆C₁的方程为x²+2y²=1；
（2）证明：由题意可设直线AB的方程为y=k₁（x+1），直线CD的方程为y=k₂（x+1）．
由

x2+2y2＝1
y＝k1

点评：
本题考点：直线与圆锥曲线的关系；恒过定点的直线．

考点点评：本题考查了圆与椭圆的标准方程，考查了直线与圆锥曲线的关系，直线与圆锥曲线的关系问题，往往需要涉及繁杂的计算，这就需要学生有较强的运算能力，属难题．

1年前查看全部

点P（x0，y0）在圆x2+y2=r2内，则直线x0x+y0y＝r2和已知圆的公共点的个数为（　　） 点P（x₀，y₀）在圆x²+y²=r²内，则直线x0x+y0y＝r2和已知圆的公共点的个数为（　　） A. 0 B. 1 C. 2 D. 不能确定 gdblshwt1年前2: mingyulan007 共回答了11个问题 | 采纳率90.9%

解题思路：先利用点到直线的距离，求得圆心到直线x₀x+y₀y=r²的距离，根据P在圆内，判断出 x₀²+y₀²＜r²，进而可知d＞r，故可知直线和圆相离．
圆心O（0，0）到直线x₀x+y₀y=r²的距离为d=
r2

x20+
y20
∵点M（x₀，y₀）在圆内，∴x₀²+y₀²＜r²，则有d＞r，
故直线和圆相离，直线与圆的公共点为0个
故选A．

点评：
本题考点：点与圆的位置关系．

考点点评：本题主要考查了直线与圆的位置关系．考查了数形结合的思想，直线与圆的位置关系的判定．解题的关键是看圆心到直线的距离与圆的半径的大小关系．

1年前查看全部

已知圆C：x2+y2=r2（r＞0）与抛物线y2=40x的准线相切，若直线l：[x/a+ yb＝1与圆C有公共 已知圆C：x²+y²=r²（r＞0）与抛物线y²=40x的准线相切，若直线l：[x/a+ y b ＝1 lijing03081年前0: 共回答了个问题 | 采纳率

查看全部

（2012•绵阳三模）已知点M（a，b）（ab≠0）是圆C：x2+y2=r2内一点，直线l是以M为中点的弦所在的直线，直 （2012•绵阳三模）已知点M（a，b）（ab≠0）是圆C：x²+y²=r²内一点，直线l是以M为中点的弦所在的直线，直线m的方程为bx-ay=r²，那么（　　） A．l⊥m且m与圆C相切 B．l∥m且m与圆C相切 C．l⊥m且m与圆C相离 D．l∥m且m与圆C相离 白魔1941年前1: 戴盆望天共回答了15个问题 | 采纳率80%

解题思路：求圆心到直线的距离，然后与a²+b²＜r²比较，可以判断直线与圆的位置关系，易得两直线的关系．
以点M为中点的弦所在的直线的斜率是-[a/b]，直线m的斜率为[b/a]，∴直线l⊥m，
∵点M（a，b）是圆x²+y²=r²内一点，∴a²+b²＜r²，
∴圆心到bx-ay=r²的距离是
r2

a2+b2＞r，故相离．
故选C．

点评：
本题考点：直线与圆的位置关系．

考点点评：本题考查直线与圆的位置关系，两条直线的位置关系，是基础题．

1年前查看全部

已知圆C：x2+y2=r2与直线3x-4y+10=0相切，则圆C的半径r=______． 抗枪打鸟1年前1: 梦幻女孩2001 共回答了19个问题 | 采纳率84.2%

解题思路：由点到直线的距离公式，算出圆心到直线3x-4y+10=0的距离d=r，即可求出半径r的值．
∵圆x²+y²=r²（r＞0）的圆心为原点、半径为r，
∴由直线3x-4y+10=0与圆x²+y²=r²（r＞0）相切，得原点到直线的距离d=r，
即r=
10

32+(-4)2=2．
故答案为：2．

点评：
本题考点：圆的切线方程．

考点点评：本题给出直线与以原点为圆心的圆相切，在已知直线方程的情况下求圆的半径．着重考查了点到直线的距离公式、直线与圆的位置关系等知识，属于基础题．

1年前查看全部

已知点P（a，b）（ab≠0）是圆x2+y2=r2内的一点，直线m是以P为中点的弦所在直线，直线l的方程为ax+by=r 已知点P（a，b）（ab≠0）是圆x2+y2=r2内的一点，直线m是以P为中点的弦所在直线，直线l的方程为ax+by=r2 已知点P（a，b）（ab≠0）是圆x²+y²=r²内的一点，直线m是以P为中点的弦所在直线，直线l的方程为ax+by=r²，那么（　　） A．m∥l，且l与圆相交 B．m⊥l，且l与圆相切 C．m∥l，且l与圆相离 D．m⊥l，且l与圆相离 阿贵阿贵阿贵1年前1: 萝卜的下属共回答了24个问题 | 采纳率100%

∵点P（a，b）（ab≠0）在圆内，
∴a²+b²＜r²，
∵k_OP=[b/a]，直线OP⊥直线m，
∴k_m=-[a/b]，
∵直线l的斜率k_l=-[a/b]=k_m，
∴m∥l，
∵圆心O到直线l的距离d=
r2

a2+b2＞
r2
r=r，
∴l与圆相离．
故选C．

1年前查看全部

若圆x2+y2=R2（R＞0）和曲线|x|3+|y|4＝1恰有六个公共点，则R的值是______． 兰湾1年前0: 共回答了个问题 | 采纳率

查看全部

已知圆C的方程为x2+y2=r2，定点M（x0，y0），直线l：x0x+y0y=r2有如下两组论断： 已知圆C的方程为x²+y²=r²，定点M（x₀，y₀），直线l：x₀x+y₀y=r²有如下两组论断： 第Ⅰ组第Ⅱ组 （a）点M在圆C内且M不为圆心（1）直线l与圆C相切 （b）点M在圆C上（2）直线l与圆C相交 （c ）点M在圆C外（3）直线l与圆C相离 由第Ⅰ组论断作为条件，第Ⅱ组论断作为结论，写出所有可能成立的命题______．（将命题用序号写成形如p⇒q的形式） cuijun1061年前1: chengjingjing_26 共回答了24个问题 | 采纳率87.5%

解题思路：根据组合规律共有9中可能：（a）⇒（1），（a）⇒（2），（a）⇒（3），（b）⇒（1），（b）⇒（2），（b）⇒（3），（c）⇒（1），（c）⇒（2），（c）⇒（3），在当中找出可能是真命题的个数即可．
9中可能有：（a）⇒（1），（a）⇒（2），（a）⇒（3），（b）⇒（1），（b）⇒（2），（b）⇒（3），（c）⇒（1），（c）⇒（2），（c）⇒（3）．所以可能是真命题的是：（a）⇒（2），（b）⇒（1），（c）⇒（3）
说明：（a）⇒（2），点M在圆C内且M不为圆心⇒直线l与圆C相交，因为直线经过M（x₀，y₀）而M在圆内，所以直线与圆相交，假如不相交，则就相切或外离得到矛盾，所以直线l与圆相交．
（b）⇒（1），点M在圆C上⇒直线l与圆C相切，点M在圆上可能直线与圆只有一个公共点，所以直线l与圆相切．
（c）⇒（3），点M在圆C外⇒直线l与圆C相离，点M在圆外，可能直线l与圆相离．

点评：
本题考点：直线与圆的位置关系；四种命题．

考点点评：考查学生掌握直线与圆的三种关系，以及灵活运用四种命题的能力．

1年前查看全部

圆的切点弦方程我是说普遍的即是（x-a）2+（y-b）2=r2的切点弦方程而不是x2+y2=r2 的切点弦方程（如果 圆的切点弦方程 我是说普遍的即是（x-a）2+（y-b）2=r2的切点弦方程而不是x2+y2=r2 的切点弦方程（如果连这个也说更好）还是是切点弦而不是公共弦方程更不是切点方程就是指过圆外一点做圆的切线肯定能做两条切线那么两条切线分别交圆于A B两点那么请问直线AB的方程 taozi1842756071年前1: 超越平凡2 共回答了11个问题 | 采纳率90.9%

如果圆是(x-a)^2+(y-b)^2=r^2,圆外一点为(s,t)的话,那么该切点弦的方程为
(a-s)x+(b-t)y=(a^2+b^2-r^2-as-bt),或
(s-a)(x-a)+(t-b)(y-b)=r^2.
求法：根据切点应该满足的方程（[切点-(s,t)]的斜率和[切点-圆心]的斜率互为负倒数；切点在圆上）得到两个切点（其复杂程度远超想象）,然后用两点式.
这是最笨的办法,也最机械,可以用计算机完成.
当然,也可以用根轴法等方法来完成.
另一种做法,相对简单一些：先求(s-a,t-b)关于x^2+y^2=r^2的切点弦,再用(x-a,y-b)代替(x,y)即可.

1年前查看全部

已知点M（a，b）（ab≠0）是圆C：x2+y2=r2内一点，直线l是以M为中点的弦所在的直线，直线m的方程是ax+by 已知点M（a，b）（ab≠0）是圆C：x²+y²=r²内一点，直线l是以M为中点的弦所在的直线，直线m的方程是ax+by=r²，那么（　　） A．l∥m且m与圆c相切 B．l⊥m且m与圆c相切 C．l∥m且m与圆c相离 D．l⊥m且m与圆c相离 wotsyou1年前1: jzhui130 共回答了20个问题 | 采纳率95%

解题思路：由条件求得直线l的斜率，再求出直线m的斜率，可得它们的斜率相等．利用点到直线的距离公式求得圆心C到直线m的距离
大于半径，由此可得l∥m且m与圆c相离．
由题意可得a²+b²＜r²，且CM⊥直线l，故直线l的斜率为[−1
KCM=-
a/b]．
直线m的方程是ax+by=r²，那么直线m的斜率为-[a/b]，圆心C到直线m的距离等于
|0+0−r2|

a2+ b2＞r，
故l∥m且m与圆c相离，
故选C．

点评：
本题考点：直线与圆的位置关系．

考点点评：本题主要考查直线和圆的位置关系，点到直线的距离公式的应用，属于中档题．

1年前查看全部

（2010•广东模拟）已知点P（a，b）（ab≠0）是圆O：x2+y2=r2内一点，直线m是以P为中点的弦所在的直线，若 （2010•广东模拟）已知点P（a，b）（ab≠0）是圆O：x²+y²=r²内一点，直线m是以P为中点的弦所在的直线，若直线n的方程为ax+by=r²，则（　　） A．m∥n且n与圆O相离 B．m∥n且n与圆O相交 C．m与n重合且n与圆O相离 D．m⊥n且n与圆O相离 风铃心语1年前1: wslyellow 共回答了14个问题 | 采纳率85.7%

解题思路：利用直线m是以P为中点的弦所在的直线可求得其斜率，进而根据直线n的方程可判断出两直线平行；表示出点到直线n的距离，根据点P在圆内判断出a，b和r的关系，进而判断出圆心到直线n的距离大于半径，判断出二者的关系是相离．
直线m是以P为中点的弦所在的直线
∴直线m⊥PO，
∴m的斜率为-[a/b]，
∵直线n的斜率为-[a/b]
∴n∥m
圆心到直线n的距离为
|r2|

a2+b2
∵P在圆内，
∴a²+b²＜r²，
∴
|r2|

a2+b2＞r
∴直线n与圆相离
故选A

点评：
本题考点：直线与圆的位置关系．

考点点评：本题主要考查了直线与圆的位置关系．直线和圆的位置关系分相交，相离，相切三种状态，常利用圆心到直线的距离与半径的大小关系来判断．

1年前查看全部

已知定圆x2+y2=r2内一点C（a，b），过C作两相互垂直的直线交圆于A、B，作长方形ACBP，求P点轨迹方程____ 已知定圆x²+y²=r²内一点C（a，b），过C作两相互垂直的直线交圆于A、B，作长方形ACBP，求P点轨迹方程______． 宝爱米咋的1年前0: 共回答了个问题 | 采纳率

查看全部

关于圆与直线的位置关系~(切点弦)过圆外一点P(a,b)做圆O：x2+y2=r2的切线,切点为A、B,求直线AB的方程. 关于圆与直线的位置关系~ (切点弦)过圆外一点P(a,b)做圆O：x2+y2=r2的切线,切点为A、B,求直线AB的方程. 设A(x1,y1),B(x2,y2),则过A点的切线为x1x+y1y=r2,　　又∵过点P(a,b)　　∴ax1+by1=r2,　　同理有ax2+by2=r2　　由以上两式可以看出A、B的坐标都满足方程ax+by=r2,它是一条直线的方程,　　又∵过两点的直线有且仅有一条,　　∴直线AB的方程为ax+by=r2. 想知道为什么过A点的切线为x1x+y1y=r2, qinyingying_5211年前1: 寒山弄笛共回答了16个问题 | 采纳率68.8%

给你一个比较详细的解答,其实这是有关圆的比较重要的知识点,建议你一定要记住
已知圆的方程是x2 + y2 = r2,求经过圆上一点M(x0,y0)的切线的方程.
解法一：利用斜率求解
设切线斜率为k,则有k*kOM=-1
因为KOM=y0/xo 所以K=-（x0/y0）
又因为过M点,所以切线为:y-y0=-（x0/y0）(x-x0)化简之后为：xox+yoy=x02+y02
又因为M点在圆上,所以x02+y02=r2所以
切线方程为：x0x+y0y=r2

1年前查看全部

点P（x0，y0）在圆x2+y2=r2内，则直线x0x+y0y＝r2和已知圆的公共点的个数为（　　） 点P（x₀，y₀）在圆x²+y²=r²内，则直线x0x+y0y＝r2和已知圆的公共点的个数为（　　） A. 0 B. 1 C. 2 D. 不能确定 e有心人1年前1: ybayba56 共回答了21个问题 | 采纳率90.5%

解题思路：先利用点到直线的距离，求得圆心到直线x₀x+y₀y=r²的距离，根据P在圆内，判断出 x₀²+y₀²＜r²，进而可知d＞r，故可知直线和圆相离．
圆心O（0，0）到直线x₀x+y₀y=r²的距离为d=
r2

x20+
y20
∵点M（x₀，y₀）在圆内，∴x₀²+y₀²＜r²，则有d＞r，
故直线和圆相离，直线与圆的公共点为0个
故选A．

点评：
本题考点：点与圆的位置关系．

考点点评：本题主要考查了直线与圆的位置关系．考查了数形结合的思想，直线与圆的位置关系的判定．解题的关键是看圆心到直线的距离与圆的半径的大小关系．

1年前查看全部

已知圆C1:x2+y2=r2(r>0)与圆C2:(x-a)2+(y-3)2=2的一条公切线方程为x+y-2=0 已知圆C1:x2+y2=r2(r>0)与圆C2:(x-a)2+(y-3)2=2的一条公切线方程为x+y-2=0 若a属于（0,正无穷）,直线l：y=x+b,试问是否存在实数b,使得直线l与两圆都相交?若存在,求出b的取值范围,若不存在,请说明理由 xiaoyi24111年前1: luying19830531 共回答了18个问题 | 采纳率94.4%

根据点到直线的距离公式,
r=|0+0-2|/√(1²+1²)=√2； |a+3-2|/√(1²+1²)=√2,(a＞0)
得 r=√2 ; a=1
所以,C1：:x²+y²=2 C2：(x-1)²+(y-3)² =2
联立:x²+y²=2和y=x+b,消 y 得 x²+(x+b)²=2,
整理得：2x²+2bx+b²-2=0,
Δ=(2b)²-4·2·(b²-2) ＞0, 解得 -2＜b＜2;
同理,联立(x-1)²+(y-3)² =2和y=x+b,解得 0＜b＜4
综上,b的取值范围为 0＜b＜2.

1年前查看全部

P(x0,y0)为圆x2+y2=r2外一点.过P点做切线PA、PB,A、B为切点.求直线AB的方程 danggui19851年前1: 坏oo0668 共回答了13个问题 | 采纳率76.9%

这个方程是 x0*x+y0*y=r^2 .
证明：设 A（a1,b1）,则过 A 的切线方程为 a1*x+b1*y=r^2 ,
由于切线过 P ,因此 a1*x0+b1*y0=r^2 ,
同理,设 B（a2,b2）,则过 B 的切线方程为 a2*x+b2*y=4^2 ,
由于切线过 P ,因此 a2*x0+b2*y0=r^2 ,
从以上两式可以看出,A、B 的坐标均满足一次方程 x0*x+y0*y=r^2 ,而它就表示直线,
因此它就是过 A、B 的直线方程 .
（这里用到一个结论：过圆 x^2+y^2=r^2 上一点（a,b）的切线方程为 ax+by=r^2 ）

1年前查看全部

过圆：x2+y2=r2外一点P（x0，y0）引此圆的两条切线，切点为A、B，则直线AB的方程为______． 盈盈酒窝孰依依1年前3: gzh3841016 共回答了13个问题 | 采纳率84.6%

解题思路：根据题意，设A（x₁，）、B（x₂，y₂），求出经过点A、点B的圆的切线分别为x₁x+y₁y=r²、x₂x+y₂y=r²．而点P是这两条直线的公共点，代入直线方程并利用比较系数法，可得所求直线AB的方程．
设A（x₁，）、B（x₂，y₂），
则设P（x，y）为过A的切线上一点，可得

AP=（x-x₁，y-y₁）
∵

AP•

OA=0，得x₁（x-x₁）+y₁（y-y₁）=0，化简得x₁x+y₁y=x₁²+y₁²
∵点A在圆x²+y²=r²上，可得x₁²+y₁²=r²
∴经过点A的圆的切线为x₁x+y₁y=r²，
同理可得经过点B的圆的切线为x₂x+y₂y=r²．
又∵点P（x₀，y₀）是两切线的交点，
∴可得x₀x₁+y₀y₁=r²，说明点A（x₁，y₁）在直线x₀x+y₀y=r²上；
同理x₀x₂+y₀y₂=r²，说明点B（x₂，y₂）在直线x₀x+y₀y=r²上
因此可得直线AB方程为：x₀x+y₀y=r²
故答案为：x₀x+y₀y=r²
点评：
本题考点：直线与圆的位置关系．

考点点评：本题求圆的切点弦所在直线方程，解题量请注意与所学过圆上一点的切线的联系，体现由不熟悉向熟悉的转化，并注意直线方程形的特点，属于中档题．

1年前查看全部

（2012•广州一模）已知圆O：x2+y2=r2，点P（a，b）（ab≠0）是圆O内一点，过点P的圆O的最短弦所在的直线 （2012•广州一模）已知圆O：x²+y²=r²，点P（a，b）（ab≠0）是圆O内一点，过点P的圆O的最短弦所在的直线为l₁，直线l₂的方程为ax+by+r²=0，那么（　　） A．l₁∥l₂，且l₂与圆O相离 B．l₁⊥l₂，且l₂与圆O相切 C．l₁∥l₂，且l₂与圆O相交 D．l₁⊥l₂，且l₂与圆O相离 ll人在纽约1年前1: chenlizhe 共回答了21个问题 | 采纳率100%

解题思路：用点斜式求得直线m的方程，与直线l的方程对比可得m∥l，利用点到直线的距离公式求得圆心到直线l的距离大于
半径 r，从而得到圆和直线l相离．
由题意可得a²+b²＜r²，OM⊥m．
∵K_OP=[b/a]，∴l₁的斜率k₁=-[a/b]．
故直线l₁的方程为 y-b=-[a/b]（x-a），即 ax+by-（a²+b²）=0．
又直线l₂的方程为ax+by+r²=0，故l₁∥l₂，
圆心到直线l₂的距离为
|0+0−r2|

a2+b2＞
r2
r=r，故圆和直线l₂相离．
故选A．

点评：
本题考点：直线与圆的位置关系；直线的一般式方程与直线的平行关系．

考点点评：本题考查点和圆、直线和圆的位置关系，点到直线的距离公式，得到圆心到直线l的距离大于半径 r，是解题的关键．

1年前查看全部

已知圆c:x2+y2=r2(r>0)与直线l:2x+y+m=0相切.(1)若m=10,求圆c的方 已知圆c:x2+y2=r2(r>0)与直线l:2x+y+m=0相切.(1)若m=10,求圆c的方 ; 面孔模糊1年前0: 共回答了个问题 | 采纳率

查看全部

若圆的方程是x2+y2=r2过圆上M（x0,y0）的切线方程是x0*x+yo*y=r2那圆心为（a,b）,过圆上M（x0 若圆的方程是x2+y2=r2 过圆上M（x0,y0）的切线方程是x0*x+yo*y=r2 那圆心为（a,b）,过圆上M（x0,y0）的切线方程是什么? 陈野1年前1: huxiaochen 共回答了18个问题 | 采纳率100%

圆心为（a,b）,过圆上M（x0,y0）的切线方程是
(x-x0)(x0-a)+(y-y0)(y0-b)=r^2[r^2=(x0-a)^2+(y0-b)^2]
利用向量垂直做比较简单

1年前查看全部

方程x2+y2=r2被直线y=3x截得弦长为6,求圆方程 lq36235411年前5: 隔岸灯火闪闪共回答了20个问题 | 采纳率100%

由题知道圆心为（0,0）,容易知道圆心在直线y=3x上,而直线y=3x截圆得弦长为6,
故圆的直径为6,推出圆的半径为3,即是：r=3
推出圆的方程为：x^2+y^2=3^2=9

1年前查看全部

已知圆的方程为x2+y2=r2，圆内有一定点P（a，b），A，B是圆周上的两个动点，PA⊥PB，求矩形APBQ的顶点Q的 已知圆的方程为x²+y²=r²，圆内有一定点P（a，b），A，B是圆周上的两个动点，PA⊥PB，求矩形APBQ的顶点Q的轨迹方程． haha255531年前0: 共回答了个问题 | 采纳率

查看全部

过圆O：X2+Y2=R2外一点M(a,b)作圆O的两条切线,P,Q为切点,则过P,Q,M三点的圆方程是?直线PQ的方程是 过圆O：X2+Y2=R2外一点M(a,b)作圆O的两条切线,P,Q为切点,则过P,Q,M三点的圆方程是?直线PQ的方程是? 要过程 jian_xia1年前1: 007晨曦共回答了14个问题 | 采纳率78.6%

连接OQ、OP,则PO⊥PM,OQ⊥PQ
所以OQPM四点共圆,且OM为直径,即圆心坐标为（a/2,b/2),半径为|OM|/2
所以圆方程为：（X-a/2)^2+(Y-b/2)^2=(a^2+b^2)/4
由（X-a/2)^2+(Y-b/2)^2=(a^2+b^2)/4
X^2+Y^2=R^2,可知
aX+bY=R^2
所以直线PQ的方程为：aX+bY-R^2=0

1年前查看全部

x2+y2=r2 的圆相切与直线y=mx+b 求证r2（1+m2）=b2 其中的2都是平分我知道可以利用点到直线距 x2+y2=r2 的圆相切与直线y=mx+b 求证r2（1+m2）=b2 其中的2都是平分我知道可以利用点到直线距离式子. 但是我需要推理出,不需要直接把点到直线距离式子换下位置就de'chu得出 每天都要戒次烟1年前3: 季节的雨滴共回答了13个问题 | 采纳率100%

联立x2+y2=r2
y=mx+b
得：m^2x^2+b^2+2mbx+x^2=r^2
x^2(m^2+1)+2mbx+b^2-r^2=0
因为相切所以直线与圆只有一个交点：
则判别式：
4m^2b^2-4(m^2+1)(b^2-r^2)=0
m^2b^2-m^2b^2+m^2r^2-b^2+r^2=0
r^2(1+m)=b^2
命题获证

1年前查看全部

设L:x2+y2=R2(R>0),则∫L(x2+y2)dx= 朱冬霞1年前1: bbt乐乐共回答了17个问题 | 采纳率94.1%

∫L(x²+y²)dx
=∫L R² dx
=R²∫L 1 dx
=2πR³
曲线积分可以用曲线方程来化简被积函数
被积函数为1,积分结果为曲线弧长,也就是圆周长.

1年前查看全部

x2+y2=r2 的圆相切与直线y=mx+b 求证r2（1+m2）=b2 其中的2都是平分我知道可以利用点到直线距 x2+y2=r2 的圆相切与直线y=mx+b 求证r2（1+m2）=b2 其中的2都是平分我知道可以利用点到直线距离式子. 但是我需要推理出,不需要直接把点到直线距离式子换下位置就de'chu得出 chimeng1年前1: jedyliu 共回答了13个问题 | 采纳率92.3%

用等面积也可以得到.
y=mx+b 化成截距式为 x/(-b/m)+y/b=1,截点为(-b/m,0)和 (0,b)
截点与原点的三角形面积为S1=1/2 |-b/m| * |b| = 1/2 b^2/|m|
而三角形的斜边长为a= V[(-b/m)^2+b^2] = V [b^2(1+1/m^2)]
因为相切,以斜为底的高为r,面积为S2=1/2 a r
S1=S2,化简后,可以得到证r2（1+m2）=b2

1年前查看全部

已知圆的方程是x2+y2=r2，求经过圆上一点M（x0，y0）的切线方程． tianyao21年前1: dwn821031 共回答了22个问题 | 采纳率86.4%

解题思路：分两种情况考虑：当切线方程的斜率不存在时，显然切线方程为x=x₀；当切线方程的斜率存在时，要求过M的切线方程，就要求直线的斜率，先根据O和M的坐标求出直线OM的斜率，根据直线与圆相切时切线垂直与经过切点的半径得到直线OM与切线垂直，即可求出切线的斜率，得到切线方程．
当切线方程的斜率不存在时，切线方程为：x=x₀；
当切线方程的斜率存在时，
由x²+y²=r²，可知圆心为原点（0，0），M（x₀，y₀），
所以直线OM的斜率k=
y0
x0，
根据所求切线与直线OM垂直得到切线的斜率k′=-
x0
y0，
则切线方程为y-y₀=-
x0
y0（x-x₀）；
即x₀x+y₀y-x₀²-y₀²=0，
综上，所求切线方程为x=x₀或x₀x+y₀y-x₀²-y₀²=0．

点评：
本题考点：圆的切线方程．

考点点评：考查学生灵活运用圆切线的性质定理，掌握两直线垂直时所满足的条件，会根据一点坐标与斜率写出直线的方程．

1年前查看全部

“过原点的直线l交圆x2+y2=r2于A，B两点，点P为圆上异于A，B的动点，若直线PA，PB的斜率均存在，则它们之积是 “过原点的直线l交圆x²+y²=r²于A，B两点，点P为圆上异于A，B的动点，若直线PA，PB的斜率均存在，则它们之积是定值-1”．类比圆的性质，可得出椭圆的一个正确结论：过原点的直线l交椭圆 x2 a2 + y2 b2 =1（a＞b＞0）于A，B两点，点P为椭圆上异于A，B的动点，若直线PA，PB的斜率均存在，则它们之积是定值 - b2 a2 - b2 a2 ． 最后一抹夕阳1年前1: 冉云朵共回答了19个问题 | 采纳率84.2%

解题思路：由圆的性质可以类比得到椭圆的类似性质．
由圆的性质可以类比得到椭圆的类似性质，即k_PM•k_PN=-
b2
a2，
证明如下：设点M的坐标为（m，n），则点N的坐标为（-m，-n），进而可知
m2
a2+
y2
b2＝1，
又设点P的坐标为（x，y），
则k_PM=[y−n/x−m]，k_PN=[y+n/x+m]
∴k_PM•k_PN=
y2−n2
x2−m2，
将y²=b^2_（1-
x2
a2），n²=b²（1-
m2
a2）代入得k_PM•k_PN=-
b2
a2．
故答案为：-
b2
a2．

点评：
本题考点：类比推理．

考点点评：类比推理的一般步骤是：（1）找出两类事物之间的相似性或一致性；（2）用一类事物的性质去推测另一类事物的性质，得出一个明确的命题（猜想）．

1年前查看全部

1.圆方程为X2+y2=r2 设x=rcosθ,y=cosθ,表示什么曲线(θ在[0,2p﹚） 1.圆方程为X2+y2=r2 设x=rcosθ,y=cosθ,表示什么曲线(θ在[0,2p﹚） 2.在直角坐标系中x=a+rcosθ y=b+rsinθ,表示什么曲线 要有详解 光脚丫的可爱宝贝1年前1: 九型人格共回答了16个问题 | 采纳率93.8%

1 圆的一条直径
2 圆心在（a,b）,半径为r的圆

1年前查看全部

点P（x0，y0）在圆x2+y2=r2内，则直线x0x+y0y＝r2和已知圆的公共点的个数为（　　） 点P（x₀，y₀）在圆x²+y²=r²内，则直线x0x+y0y＝r2和已知圆的公共点的个数为（　　） A. 0 B. 1 C. 2 D. 不能确定 总有那么一天1年前1: 我在等待幸福降临共回答了25个问题 | 采纳率92%

解题思路：先利用点到直线的距离，求得圆心到直线x₀x+y₀y=r²的距离，根据P在圆内，判断出 x₀²+y₀²＜r²，进而可知d＞r，故可知直线和圆相离．
圆心O（0，0）到直线x₀x+y₀y=r²的距离为d=
r2

x20+
y20
∵点M（x₀，y₀）在圆内，∴x₀²+y₀²＜r²，则有d＞r，
故直线和圆相离，直线与圆的公共点为0个
故选A．

点评：
本题考点：点与圆的位置关系．

考点点评：本题主要考查了直线与圆的位置关系．考查了数形结合的思想，直线与圆的位置关系的判定．解题的关键是看圆心到直线的距离与圆的半径的大小关系．

1年前查看全部

已知点P（a，b）（ab≠0）是圆x2+y2=r2内的一点，直线m是以P为中点的弦所在直线，直线l的方程为ax+by=r 已知点P（a，b）（ab≠0）是圆x²+y²=r²内的一点，直线m是以P为中点的弦所在直线，直线l的方程为ax+by=r²，那么（　　） A. m∥l，且l与圆相交 B. m⊥l，且l与圆相切 C. m∥l，且l与圆相离 D. m⊥l，且l与圆相离 往事都是错1年前3: 风中的花朵共回答了19个问题 | 采纳率89.5%

解题思路：由P在圆内，得到P到圆心距离小于半径，利用两点间的距离公式列出不等式a²+b²＜r²，由直线m是以P为中点的弦所在直线，利用垂径定理得到直线OP与直线m垂直，根据直线OP的斜率求出直线m的斜率，再表示出直线l的斜率，发现直线m与l斜率相同，可得出两直线平行，利用点到直线的距离公式表示出圆心到直线l的距离，利用得出的不等式变形判断出d大于r，即可确定出直线l与圆相离．
∵点P（a，b）（ab≠0）在圆内，
∴a²+b²＜r²，
∵k_OP=[b/a]，直线OP⊥直线m，
∴k_m=-[a/b]，
∵直线l的斜率k_l=-[a/b]=k_m，
∴m∥l，
∵圆心O到直线l的距离d=
r2

a2+b2＞
r2
r=r，
∴l与圆相离．
故选C．

点评：
本题考点：直线与圆的位置关系．

考点点评：此题考查了直线与圆的位置关系，涉及的知识有：两点间的距离公式，点到直线的距离公式，两直线垂直、平行时直线斜率满足的关系，直线与圆的位置关系由d与r的大小来判断，当d＞r时，直线与圆相离；当d＜r时，直线与圆相交；当d=r时，直线与圆相切（其中d为圆心到直线的距离，r为圆的半径）．

1年前查看全部

圆的切点弦方程我是说普遍的即是（x-a）2+（y-b）2=r2的切点弦方程而不是x2+y2=r2的切点弦方程（如果连 圆的切点弦方程 我是说普遍的即是（x-a）2+（y-b）2=r2的切点弦方程而不是x2+y2=r2 的切点弦方程（如果连这个也说更好）还是是切点弦而不是公共弦方程 久ee1年前3: 只用一次的小rr 共回答了13个问题 | 采纳率92.3%

不是哦,（x-a）2+（y-b）2=r2的切点弦方程是（x-a)(x0-a)+(y-a)(y0-a)=r2
a b就是圆心坐标x0 y0是过圆外点P的坐标,如果P在圆上就是过点P的切线了,只有一条.当a=b=0的时候就是你说的那种原点情况啦.
祝学习愉快!

1年前查看全部

已知圆o:x2+y2=r2上的点…… icediant1年前1: yangshuli 共回答了12个问题 | 采纳率100%

上式原
f的衍生物的两侧'（X）= 2X + 2×（F'（1））'+ 2F'（1）
为f（1）必须有一个特定值“,这是一个常数.因此,（F'（1））'= 0,
F'（X）= 2X + 2F'（1）
因此f'（0）= 2F'（1）
然后使X = 1,我们得到F'（1）= 2 + 2F'（1）,使得F'（1）= - 2,
因此f'（0）= - 4

1年前查看全部

点p（x1,y1）在圆x2+y2=r2内,则直线x1x+y1y=r2与已知圆的公共点的个数

共1条回复

相关推荐

大家在问