“三等分角”是数学史上一个著名的问题,但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给出的一种“三等分锐角”的
 Alan_love_u20002022-10-04 11:39:541条回答
Alan_love_u20002022-10-04 11:39:541条回答 “三等分角”是数学史上一个著名的问题,但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法(如图):将给定的锐角∠AOB置于直角坐标系中,边OB在x轴上、边OA与函数y=
(1)设P(a,
(2)分别过点P和R作y轴和x轴的平行线,两直线相交于点Q.请说明Q点在直线OM上,并据此证明  ∠MOB=
(3)应用上述方法得到的结论,你如何三等分一个钝角(用文字简要说明). |

已提交,审核后显示!提交回复
共1条回复
 漠然一笑 共回答了19个问题
漠然一笑 共回答了19个问题 |采纳率89.5%- (1)设直线OM的函数关系式为y=kx,P(a,
1
a )、R(b,
1
b ).(1分)
则M(b,
1
a ),
∴k=
1
a ÷b=
1
ab .(2分)
∴直线OM的函数关系式为y=
1
ab x.(3分)
(2)∵Q的坐标(a,
1
b ),满足y=
1
ab x,
∴点Q在直线OM上.
∵四边形PQRM是矩形,
∴SP=SQ=SR=SM=
1
2 PR.
∴∠SQR=∠SRQ.(5分)
∵PR=2OP,
∴PS=OP=
1
2 PR.
∴∠POS=∠PSO.(6分)
∵∠PSQ是△SQR的一个外角,
∴∠PSQ=2∠SQR.
∴∠POS=2∠SQR.(7分)
∵QR ∥ OB,
∴∠MOB=∠SQR.(8分)
∴∠POS=2∠MOB.(9分)
∴∠MOB=
1
3 ∠AOB.(10分)
(3)①先做出钝角的一半,按照上述方法先将此钝角的一半(锐角)三等分,进而做出再做一个角与已做得的角相等即可得到钝角的三等分角.
②先作钝角的邻补角的三等分角,然后再以得到的三等分角作等边三角形可得钝角的三等分角,在钝角内作做出这个角即可. - 1年前
相关推荐
- 已知正方形abcd,菱形acef,连接af,de,ae,e,f,d在一直线上,求证:ae,af三等分角cad
 边看边想1年前1
边看边想1年前1 -
 ss751213 共回答了17个问题
ss751213 共回答了17个问题 |采纳率94.1%首先因为是菱形,AE平分角CAF,所以我们只要证明CAF是CAD的三分之二就行了.CAD是45度,所以我们要证CAF是30度.
由C作垂线交ED于H.因为DE平行于AC,CDH是45度,所以CHD是等腰三角形,并且CH=AC/2.由于AC=CE,CH=CE/2.也就是说,CHE的斜边是短边的二倍,即CHE是30-60-90三角形.CEH是30度,那么CAF也是30度.1年前查看全部
- 怎么用心脏线三等分任意角?人们说在研究「三等分角」的过程中发现了如蚌线、心脏线、圆锥曲线等特殊曲线,这些曲线也可以解决三
怎么用心脏线三等分任意角?
人们说在研究「三等分角」的过程中发现了如蚌线、心脏线、圆锥曲线等特殊曲线,这些曲线也可以解决三等分角问题。但具体怎么解决呢?
用这么多分悬赏,难道没一个人知道?
不要所问非所答!这不是尺规作图问题 wjhxf6041年前7
wjhxf6041年前7 -
 无意江湖者 共回答了21个问题
无意江湖者 共回答了21个问题 |采纳率85.7%lz请看
无法完成3等分一个角
除非用特殊得工具
平面几何作图限制只能用直尺、圆规,而这里所谓的直尺是指没有刻度只能画直线的尺.用直尺与圆规当然可以做出许多种之图形,但有些图形如正七边形、正九边形就做不出来.有些问题看起来好像很简单,但真正做出来却很困难,这些问题之中最有名的就是所谓的三大问题.
三大几何问题是:
1.化圆为方-求作一正方形使其面积等於一已知圆;
2.三等分任意角;
3.倍立方-求作一立方体使其体积是一已知立方体的二倍.
圆与正方形都是常见的几何图形,但如何作一个正方形和已知圆等面积呢?若已知圆的半径为1则其面积为π(1)2=π,所以化圆为方的问题等於去求一正方形其面积为π,也就是用尺规做出长度为π1/2的线段(或者是π的线段).
三大问题的第二个是三等分一个角的问题.对於某些角如90.、180.三等分并不难,但是否所有角都可以三等分呢?例如60.,若能三等分则可以做出20.的角,那麽正18边形及正九边形也都可以做出来了(注:圆内接一正十八边形每一边所对的圆周角为360./18=20.).其实三等分角的问题是由求作正多边形这一类问题所引起来的.
第三个问题是倍立方.埃拉托塞尼(公元前276年~公元前195年)曾经记述一个神话提到说有一个先知者得到神谕必须将立方形的祭坛的体积加倍,有人主张将每边长加倍,但我们都知道那是错误的,因为体积已经变成原来的8倍.
这些问题困扰数学家一千多年都不得其解,而实际上这三大问题都不可能用直尺圆规经有限步骤可解决的.
1637年笛卡儿创建解析几何以后,许多几何问题都可以转化为代数问题来研究.1837年旺策尔(Wantzel)给出三等分任一角及倍立方不可能用尺规作图的证明.1882年林得曼(Linderman)也证明了π的超越性(即π不为任何整数系数多次式的根),化圆为方的不可能性也得以确立.1年前查看全部
- 条件:一支笔,一把没有刻度的尺子,一个圆规.画任意角的三等分角!
条件:一支笔,一把没有刻度的尺子,一个圆规.画任意角的三等分角!
--困惑好多年! sung311年前2
sung311年前2 -
 kentjinqiu 共回答了12个问题
kentjinqiu 共回答了12个问题 |采纳率91.7%尺规作图不可能三等分任意角的.这是经数学证明了的!1年前查看全部
- 假如说有人破解了三等分角难题会获的什么样的奖励啊?
假如说有人破解了三等分角难题会获的什么样的奖励啊?
假如,只是假如!这道题在世界数学史上的地位如何啊?如果说他真的破解了会怎样啊?
我只是说假设啊!我知道不可能的,只是想知道会如果他仅用尺规解决这一难题,有什么样的奖励。想像一下嘛,告诉我一个答案吧! KILLUA_7771年前1
KILLUA_7771年前1 -
 torubleqq 共回答了17个问题
torubleqq 共回答了17个问题 |采纳率100%标准的说法应该是,在只有尺规的情况下3等分任意角吧.已经证明不可能,如果有人做到了,他可以算上数学界的爱因斯坦了,当今的数学大厦也将为之倾倒.1年前查看全部
- 数学人教A版这些选修都讲什么?选修3-2:信息安全与密码选修3-5:欧拉公式与闭曲面分类选修3-6:三等分角与数域扩充选
数学人教A版这些选修都讲什么?
选修3-2:信息安全与密码
选修3-5:欧拉公式与闭曲面分类
选修3-6:三等分角与数域扩充
选修4-3:数列与差分
选修4-8:统筹法与图论初步
选修4-10:开关电路与布尔代数
再顺便问一下,在长春能不能买到选修4-9:风险与决策?找了很多新华书店都没有 恒等式法1年前1
恒等式法1年前1 -
 ll化 共回答了22个问题
ll化 共回答了22个问题 |采纳率95.5%选修3-2:密码概率不分家,首先从老朋友概率说起.而密码既然是一串数字(或含字母),又跑不了数论(拉格朗日插值法之类的).再讲一讲常用的明密转换,加密方法,历史事例,各种应用(凯撒是第一个尝试者).
选修3-5:对于凸多面体而言,必有公式:V+F-E=2,其中V是多面体P的顶点个数,F是多面体P的面数,E是多面体P的棱的条数,X(P)是多面体P的欧拉示性数.如果P可以同胚于一个球面(可以通俗地理解为能吹胀而绷在一个球面上),那么X(P)=2,包括我们经常讲的凸多面体.这里与拓扑学有关,所以先给你讲拓扑学.再来给你讲这个公式.
选修3-6:想当初初中搞的是尺规等分角.吃饱了撑的希腊人又搞了这么几个问题:三等分角,倍立方,等面积化圆为方,就让你用尺规.在大部分人有事干的今天,人们看的是别的问题(1895年伟大的数学家克莱因证明了这三个问题无解).那么为什么无解又站在了研究第一线,引用了N多定理.再说数域.设F是一个数环,如果对任意的a,b∈F而且a≠0,则b/a∈F;则称F是一个数域.例如有理数集、实数集、复数集等都是数域.(数环:设S是复数集的非空子集,如果S中的数对任意两个数的和、差、积仍属于S,则称S是一个数环.例如整数集Z就是一个数环,有理数集Q、实数集R、复数集C等都是数环.)现在我们要出发,甩掉QRC进入新世界.
选修4-3:数列也是函数,这不可否认.只不过它的定义域是正整数罢了.而我们无论是讲导数,还是讲积分,还是讲微分,还是讲极限来研究导数,统统地有一个前提:“如无特别说明,本题所涉函数皆为连续函数.”讲得十分清楚.连续必可导可导必连续啊,这是一元函数微分学的一个重要结论.我们知道导数是用极限定义的,那么对于数列这一类函数(离散函数)又怎么办?
定义:Δf(x)=[f(x+1)-f(x)]为离散函数的一阶差分,类似于导数还可以有高阶差分.含有未知函数差分的方程称差分方程.同样地有方程特定的解法.同时,有差分,就有逆差分.这里的Δ,是差分算子,有他独特的性质.
选修4-8:统筹是一门学问.别看国家部门多职能·多,本质上它们都要统筹,还有专门的学科统筹学.统筹方法中的基本模型,是统筹图(网络图).没了图统筹会很不直观.它是用节点、箭头和与之相应的数来描述整体和各部分、各部分之间以及它们和外界之间的关系.从基本模型出发,根据不同的整体目标,还需选取与之相适应的其他模型.
由此引发图论的问题那也是自然而然的(看图说话).最早的图论实例,大概就是七桥问题.在这之后还有四色地图问题.它可以脱离统筹,自己去搞一些应用.
选修4-10:物理3-1中有那么一节,讲的是逻辑电路.
什么是布尔代数?所谓一个布尔代数(也称逻辑代数),是指一个有序的四元组〈B,∨,∧,*〉,其中B是一个非空的集合,∨与∧是定义在B上的两个二元运算,*是定义在B上的一个一元运算,并且它们满足一定的条件,就能构成布尔代数.说俩名词:与逻辑,或逻辑,然后你一定会想到一些东西(若你是理科的).太深的不说,我们用的就是这个.我们可以摆脱开关,只要有一个逻辑运算,就能算出花来.
选修4-9东北都是没有的(因为不学),只能从北京(或南方)的(淘宝)店里买.刚才说的这些书,中小学教材审核委员会还没审完呢,自然就没有.最新的,是选修3-3(2011初审过).1年前查看全部
- 急,在▲ABC中,BE、BP三等分角ABC,CE、CP三等分角ACB,急求角BPE大小
急,在▲ABC中,BE、BP三等分角ABC,CE、CP三等分角ACB,急求角BPE大小
急:在▲ABC中,BE、BP三等分角ABC,CE、CP三等分角ACB,急求角BPE大小.不能从别人那抄,我看过了,都是错的 我是美儿1年前2
我是美儿1年前2 -
 小苏东坡 共回答了21个问题
小苏东坡 共回答了21个问题 |采纳率81%如图,当∠ACB=60°时,∵∠CP、CE三等分∠ACB,∴CP平分∠ECB,∠ECB=2/3∠ACB=40°,同理,BP平分∠EBP,∴△BCE中,点P是角平分线BP、CP的交点,∴EP平分∠BEC(三角形的三条角平分线交于一点)∵∠EBC+∠BEC=180°-∠BCE=...1年前查看全部
- (2005•佛山)“三等分角”是数学史上一个著名的问题,但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给出的一
(2005•佛山)“三等分角”是数学史上一个著名的问题,但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法(如图):将给定的锐角∠AOB置于直角坐标系中,边OB在x轴上、边OA与函数y=
的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=1 x
∠AOB.要明白帕普斯的方法,请研究以下问题:1 3
(1)设P(a,
)、R(b,1 a
),求直线OM对应的函数表达式(用含a,b的代数式表示);1 b
(2)分别过点P和R作y轴和x轴的平行线,两直线相交于点Q.请说明Q点在直线OM上,并据此证明 ∠MOB=
∠MOB=
∠AOB;1 3
(3)应用上述方法得到的结论,你如何三等分一个钝角(用文字简要说明). profile3301年前1
profile3301年前1 -
 南方寒士f 共回答了24个问题
南方寒士f 共回答了24个问题 |采纳率100%(1)设直线OM的函数关系式为y=kx,P(a,
1
a)、R(b,
1
b).(1分)
则M(b,
1
a),
∴k=
1
a÷b=
1
ab.(2分)
∴直线OM的函数关系式为y=
1
abx.(3分)
(2)∵Q的坐标(a,
1
b),满足y=
1
abx,
∴点Q在直线OM上.
∵四边形PQRM是矩形,
∴SP=SQ=SR=SM=
1
2PR.
∴∠SQR=∠SRQ.(5分)
∵PR=2OP,
∴PS=OP=
1
2PR.
∴∠POS=∠PSO.(6分)
∵∠PSQ是△SQR的一个外角,
∴∠PSQ=2∠SQR.
∴∠POS=2∠SQR.(7分)
∵QR∥OB,
∴∠MOB=∠SQR.(8分)
∴∠POS=2∠MOB.(9分)
∴∠MOB=
1
3∠AOB.(10分)
(3)①先做出钝角的一半,按照上述方法先将此钝角的一半(锐角)三等分,进而做出再做一个角与已做得的角相等即可得到钝角的三等分角.
②先作钝角的邻补角的三等分角,然后再以得到的三等分角作等边三角形可得钝角的三等分角,在钝角内作做出这个角即可.1年前查看全部
- 尺规真的不能三等分角吗?求证明.
尺规真的不能三等分角吗?求证明.
是不是只要用没有标刻的尺子,圆规把任意的已知角三等分,就算成功吗? ba8111年前0
ba8111年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 三角形ABC中,角A等于60度,BP.BE三等分角ABC,CP.CE三等分角ACB,求角BPE
 dyqdyqdq1年前5
dyqdyqdq1年前5 -
 irene_Q 共回答了30个问题
irene_Q 共回答了30个问题 |采纳率90%1年前查看全部
- 三等分角真的不能分吗?其实任意角可以任意等分,只用尺规
三等分角真的不能分吗?其实任意角可以任意等分,只用尺规
我可以用尺规任意等分任意角 发光的腰带1年前2
发光的腰带1年前2 -
 guyunfeiyang 共回答了20个问题
guyunfeiyang 共回答了20个问题 |采纳率90%三等分任意角的题也许比另外两个几何问题出现更早,早到历史上找不出有关的记载来.但无疑地它的出现是很自然的,就是我们自己在现在也可以想得到的.纪元前五、六百年间希腊的数学家们就已经想到了二等分任意角的方法,正像我们在几何课本或几何画中所学的:以已知角的顶点为圆心,用适当的半径作弧交角两的两边得两个交点,再分别以这两点为圆心,用一个适当的长作半径画弧,这两弧的交点与角顶相连就把已知角分为二等分.二等分一个已知角既是这么容易,很自然地会把问题略变一下:三等分怎么样呢?这样,这一个问题就这么非常自然地出现了.
现已证明,在尺规作图的前提下,此题无解.
三等分角的历史:
公元前4世纪,托勒密一世定都亚历山大城.他凭借优越的地理环境,发展海上贸易和手工艺,奖励学术.他建造了规模宏大的“艺神之宫”,作为学术研究和教学中心;他又建造了著名的亚历山大图书馆,藏书75万卷.托勒密一世深深懂得发展科学文化的重要意义,他邀请著名学者到亚历山大城,当时许多著名的希腊数学家都来到了这个城市.
亚历山大城郊有一座圆形的别墅,里面住着一位公主.圆形别墅中间有一条河,公主的居室正好建立在圆心处.别墅南北围墙各开了一个门,河上建了一座桥,桥的位置和南北门位置恰好在一条直线上.国王每天赏赐的物品,从北门运进,先放到南门处的仓库,然后公主再派人从南门取回居室.
一天,公主问侍从:“从北门到我的卧室,和从北门到桥,哪一段路更远?”侍从不知道,赶紧去测量,结果是两段路一样远的.
过了几年,公主的妹妹小公主长大了,国王也要为她修建一座别墅.小公主提出她的别墅要修的像姐姐的别墅那样,有河,有桥,有南北门.国王满口答应,小公主的别墅很快就动工了,当把南门建立好,要确定桥和北门的位置时,却出现了一个问题:怎样才能使得北门到卧室和北门到桥的距离一样远呢?
设,北门的位置为Q,南门的位置为P,卧室(圆心)为O,桥为K,
要确定北门的和桥的位置,关键是做出∠OPQ,设PO和河流的夹角是α
由 QK=QO,
得 ∠QKO=∠QOK
但是∠QKO=α+∠KPO,
又∠OQK=∠OPK
所以在△QKO中,
∠QKO+∠QOK+∠OQK
=(α+∠KPO)+(α+∠KPO)+∠KPO
=3∠KPO+2α=π
即∠KPO=(π-2α)/3
只要能把180-2α这个角三等分,就能够确定出桥和北门的位置了.解决问题的关键是如何三等分一个角.
工匠们试图用尺规作图法确定出桥的位置,可是他们用了很长的时间也没有解决.于是他们去请教阿基米德.
阿基米德用在直尺上做固定标记的方法,解决了三等分一角的问题,从而确定了北门的位置.正当大家称赞阿基米德了不起时,阿基米德却说:“这个确定北门位置的方法固然可行,但只是权宜之计,它是有破绽的.”阿基米德所谓的破绽就是在尺上做了标记,等于是做了刻度,这在尺规做图法则中是不允许的.
这个故事提出了一个数学问题:如何尺规三等分任意已知角,这个问题连阿基米德都没有解答出来.1年前查看全部
- 从o点引4条射线oa、ob、oc、od,若oe平分角boc,of、og三等分角cod,求角eog
 木p木同学1年前1
木p木同学1年前1 -
 8月天晴 共回答了17个问题
8月天晴 共回答了17个问题 |采纳率94.1%由题意
oe平分角boc则∠eoc=∠boc/2;
of、og三等分角cod则∠cod=3∠cof=3∠fog=3∠god
∠eog=∠eoc+∠cof+∠fog
∠eog=(∠boc/2)+(2∠cod)/3.1年前查看全部
- 三等分角把角画成等腰的 然后把底三等分 再连接 不就行了
 并使用1年前2
并使用1年前2 -
 shaofeng5566 共回答了15个问题
shaofeng5566 共回答了15个问题 |采纳率80%你再研究一下
那三条线段对的角不都相等,两边的等,与中间的不相等.1年前查看全部
- 怎么证明三等分角
 r5111年前1
r5111年前1 -
 qwe2009 共回答了18个问题
qwe2009 共回答了18个问题 |采纳率88.9%古希腊三个著名问题之一的三等分角,现在美国就连许多没学过数学的人也都知道.美国的数学杂志社和以教书为职业的数学会员,每年总要收到许多“角的三等分者”的来信;并且,在报纸上常见到:某人已经最终地“解决了”这个不可捉摸的问题.这个问题确实是三个著名的问题中最容易理解的一个,因为二等分角是那么容易,这就自然会使人们想到三等分角为什么不同样的容易呢?
用欧几里得工具,将一线段任意等分是件简单的事;也许古希腊人在求解类似的任意等分角的问题时,提出了三等分角问题;也许(更有可能)这问题是在作正九边形时产生的,在那里,要三等分一个60°角.
在研究三等分角问题时,看来希腊人首先把它们归结成所谓斜向(verging problem)问题.任何锐角ABC(参看图31)可被取作矩形BCAD的对角线BA和边BC的夹角.考虑过B点的一条线,它交CA于E,交DA之延长线于F,且使得EF=2(BA).令G为EF之中点,则
EG=GF=GA=BA,
从中得到:
∠ABG=∠AGB=∠GAF+∠GFA=2∠GFA=2∠GBC,
并且BEF三等分∠ABC.因此,这个问题被归结为在DA的延长线和AC之间,作一给定长度2(BA)的线段EF,使得EF斜向B点.
如果与欧几里得的假定相反,允许在我们的直尺上标出一线段E’F’=2(BA),然后调整直尺的位置,使得它过B点,并且,E’在AC上,F’在DA的延长线上;则∠ABC被三等分.对直尺的这种不按规定的使用,也可以看作是:插入原则(the insertion principle)的一种应用.这一原则的其它应用,参看问题研究4.6.
为了解三等分角归结成的斜向问题,有许多高次平面曲线已被发现.这些高次平面曲线中最古老的一个是尼科梅德斯(约公元前240年)发现的蚌线.设c为一条直线,而O为c外任何一点,P为c上任何一点,在PO的延长线上截PQ等于给定的固定长度k.于是,当P沿着c移动时,Q的轨迹是c对于极点O和常数k的蚌线(conchoid)(实际上,只是该蚌线的一支).设计个画蚌线的工具并不难①,用这样一个工具,就可以很容易地三等分角.这样,令∠AOB为任何给定的锐角,作直线MN垂直于OA,截OA于D,截OB于L(如图32所示).然后,对极点O和常数2(OL),作MN的蚌线.在L点作OA的平行线,交蚌线于C.则OC三等分∠AOB.
借助于二次曲线可以三等分一个一般的角,早期希腊人还不知道这一方法.对于这种方法的最早证明是帕普斯(Pappus,约公元300年).利用二次曲线三等分角的两种方法在问题研究4.8中可以找到.
有一些超越(非代数的)曲线,它们不仅能够对一个给定的角三等分,而且能任意等分.在这这样的曲线中有:伊利斯的希皮阿斯(Hippias,约公元前425年)发明的割圆曲线(quadratrix)和阿基米得螺线(spiral of Archimeds).这两种曲线也能解圆的求积问题.关于割圆曲线在三等分角和化圆为方问题上的应用,见问题研究4.10.
多年来,为了解三等分角问题,已经设计出许多机械装置、联动机械和复合圆规.①参看R.C.Yates.The Trisection Prolem.其中有一个有趣的工具叫做战斧,不知道是谁发明的,但是在1835年的一本书中讲述了这种工具.要制做一个战斧,先从被点S和T三等分的线段RU开始,以SU为直径作一半圆,再作SV垂直于RU,如图33所示.用战斧三等分∠ABC时,将这一工具放在该角上,使R落在BA上,SV通过B点,半圆与BC相切于D.于是证明:△RSB,△TSB,△TDB都全等,所以,BS和BT三等分给定的角.可以用直尺和圆规在描图纸上绘出战斧,然后调整到给定的角上.在这种条件下,我们可以说用直角和圆规三等分一个角(用两个战斧,则可以五等分一个角).
欧几里得工具虽然不能精确地三等分任意角,但是用这些工具的作图方法,能作出相当好的近似的三等分.一个卓越的例子是著名的蚀刻师、画家A.丢勒(Albrecht Durer)于1525年给出的作图方法.取给定的∠AOB为一个圆的圆心角(参看图34),设C为弦AB的靠近B点的三等分点.在C点作AB的垂线交圆于D.以B为圆心,以BD为半径,作弧交AB于E.设令F为EC的靠近E点的三等分点,再以B为圆心,以BF为半径,作弧交圆于G.那么,OG就是∠AOB的近似的三等分线.我们能够证明:三等分中的误差随着∠AOB的增大而增大;但是,对于60°的角大约只差1〃,对于90°角大约只差18〃.1年前查看全部
- 如何三等分角圆规 无刻度尺
 情迷拉丁1年前2
情迷拉丁1年前2 -
 孟婆靓汤 共回答了20个问题
孟婆靓汤 共回答了20个问题 |采纳率90%古希腊三个著名问题之一的三等分角,现在美国就连许多没学过数学的人也都知道.美国的数学杂志社和以教书为职业的数学会员,每年总要收到许多“角的三等分者”的来信;并且,在报纸上常见到:某人已经最终地“解决了”这个不可捉摸的问题.这个问题确实是三个著名的问题中最容易理解的一个,因为二等分角是那么容易,这就自然会使人们想到三等分角为什么不同样的容易呢?
用欧几里得工具,将一线段任意等分是件简单的事;也许古希腊人在求解类似的任意等分角的问题时,提出了三等分角问题;也许(更有可能)这问题是在作正九边形时产生的,在那里,要三等分一个60°角.
在研究三等分角问题时,看来希腊人首先把它们归结成所谓斜向(verging problem)问题.任何锐角ABC(参看图31)可被取作矩形BCAD的对角线BA和边BC的夹角.考虑过B点的一条线,它交CA于E,交DA之延长线于F,且使得EF=2(BA).令G为EF之中点,则
EG=GF=GA=BA,
从中得到:
∠ABG=∠AGB=∠GAF+∠GFA=2∠GFA=2∠GBC,
并且BEF三等分∠ABC.因此,这个问题被归结为在DA的延长线和AC之间,作一给定长度2(BA)的线段EF,使得EF斜向B点.
如果与欧几里得的假定相反,允许在我们的直尺上标出一线段E’F’=2(BA),然后调整直尺的位置,使得它过B点,并且,E’在AC上,F’在DA的延长线上;则∠ABC被三等分.对直尺的这种不按规定的使用,也可以看作是:插入原则(the insertion principle)的一种应用.这一原则的其它应用,参看问题研究4.6.
为了解三等分角归结成的斜向问题,有许多高次平面曲线已被发现.这些高次平面曲线中最古老的一个是尼科梅德斯(约公元前240年)发现的蚌线.设c为一条直线,而O为c外任何一点,P为c上任何一点,在PO的延长线上截PQ等于给定的固定长度k.于是,当P沿着c移动时,Q的轨迹是c对于极点O和常数k的蚌线(conchoid)(实际上,只是该蚌线的一支).设计个画蚌线的工具并不难①,用这样一个工具,就可以很容易地三等分角.这样,令∠AOB为任何给定的锐角,作直线MN垂直于OA,截OA于D,截OB于L(如图32所示).然后,对极点O和常数2(OL),作MN的蚌线.在L点作OA的平行线,交蚌线于C.则OC三等分∠AOB.
借助于二次曲线可以三等分一个一般的角,早期希腊人还不知道这一方法.对于这种方法的最早证明是帕普斯(Pappus,约公元300年).利用二次曲线三等分角的两种方法在问题研究4.8中可以找到.
有一些超越(非代数的)曲线,它们不仅能够对一个给定的角三等分,而且能任意等分.在这这样的曲线中有:伊利斯的希皮阿斯(Hippias,约公元前425年)发明的割圆曲线(quadratrix)和阿基米得螺线(spiral of Archimeds).这两种曲线也能解圆的求积问题.关于割圆曲线在三等分角和化圆为方问题上的应用,见问题研究4.10.
多年来,为了解三等分角问题,已经设计出许多机械装置、联动机械和复合圆规.①参看R.C.Yates.The Trisection Prolem.其中有一个有趣的工具叫做战斧,不知道是谁发明的,但是在1835年的一本书中讲述了这种工具.要制做一个战斧,先从被点S和T三等分的线段RU开始,以SU为直径作一半圆,再作SV垂直于RU,如图33所示.用战斧三等分∠ABC时,将这一工具放在该角上,使R落在BA上,SV通过B点,半圆与BC相切于D.于是证明:△RSB,△TSB,△TDB都全等,所以,BS和BT三等分给定的角.可以用直尺和圆规在描图纸上绘出战斧,然后调整到给定的角上.在这种条件下,我们可以说用直角和圆规三等分一个角(用两个战斧,则可以五等分一个角).
欧几里得工具虽然不能精确地三等分任意角,但是用这些工具的作图方法,能作出相当好的近似的三等分.一个卓越的例子是著名的蚀刻师、画家A.丢勒(Albrecht Durer)于1525年给出的作图方法.取给定的∠AOB为一个圆的圆心角(参看图34),设C为弦AB的靠近B点的三等分点.在C点作AB的垂线交圆于D.以B为圆心,以BD为半径,作弧交AB于E.设令F为EC的靠近E点的三等分点,再以B为圆心,以BF为半径,作弧交圆于G.那么,OG就是∠AOB的近似的三等分线.我们能够证明:三等分中的误差随着∠AOB的增大而增大;但是,对于60°的角大约只差1〃,对于90°角大约只差18〃.1年前查看全部
- (1)“三等分角”是数学史上一个著名问题,但数学家已经证明,仅用尺规不可能“三等分任意角”,但对于
(1)“三等分角”是数学史上一个著名问题,但数学家已经证明,仅用尺规不可能“三等分任意角”,但对于
(1)“三等分角”是数学史上一个著名问题,但数学家已经证明,仅用尺规不可能“三等分任意角”,但对于特定度数的已知角,如90°角、45°角等,是可以用尺规进行三等分的,如图a,∠AOB=90°,我们在边OB上取一点C,用尺规以OC为一边向∠AOB内部作等边△OCD,作射线OD,再用尺规作出∠DOB的角平分线OE,则射线OD、OE将∠AOB三等分,仔细体会一下其中的道理,然后用尺规把图b中的∠MON三等分(已知∠MON=45°);(不需写作法,但需保留作图痕迹,允许适当添加文字的说明) 
(2)数学家帕普斯借助函数给出了一种“三等分锐角”的方法(如图c):将给定的锐角∠AOB置于直角坐标系中,边OB在x轴上、边OA与函数  的图象交于点P,以P为圆心、2OP长为半径作弧交图象于点R, 分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=
的图象交于点P,以P为圆心、2OP长为半径作弧交图象于点R, 分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB= ∠AOB,要明白帕普斯的方法,请研究以下问题:
∠AOB,要明白帕普斯的方法,请研究以下问题:
①设 、
、 ,求直线OM对应的函数关系式(用含a、b的代数式表示);
,求直线OM对应的函数关系式(用含a、b的代数式表示);
②分别过点P和R作y轴和x轴的平行线,两直线相交于点Q,请说明Q点在直线OM上,并据此证明∠MOB= ∠AOB。
∠AOB。
 不著一字尽得风流1年前1
不著一字尽得风流1年前1 -
 laoman450 共回答了21个问题
laoman450 共回答了21个问题 |采纳率81%(1) ,
,
我们在边ON上取一点A,用尺规以OA为一边向∠MON的外部作等边△OAB,用尺规作出∠AOB的角平分线OC,再用尺规作出∠CON的角平分线OD,则射线OD、OC将∠MON三等分;
(2)①因为P(a, ),R(b,
),R(b, )且是分别过点P和R作x轴和y轴的平行线;
)且是分别过点P和R作x轴和y轴的平行线;
所以M(b, )
)
设OM的函数表达式为y=kx, ,
,
所以y= ;
;
②因为P(a,1/a),R(b,1/b)且是分别过点P和R作x轴和y轴的平行线
所以Q(a,1/b)
因为Q在OM上,
所以把Q(a,y)代入y=x/ab,y=1/b
因为1/b=1/b,
所以Q在OM上易证得四边形PQRM为矩形
所以PS=RS=OS=MS
所以∠SQR=∠SRQ,
因为∠PSQ为△SQR外角
所以∠PSQ=2∠SQR,
因为QR平行于x轴,
所以∠SQR=∠SOH
因为PR=2PO,
所以PO=PS
所以∠PSQ=∠POS,
所以∠POS=2∠SQR
所以∠POS=2∠SOH,
所以∠MOB= ∠AOB。
1年前查看全部
∠AOB。
1年前查看全部
- (2013•江东区模拟)数学家已证明“不能用直尺和圆规三等分角”.如果不限作图工具呢?有位数学爱好者制作了如下的“三等分
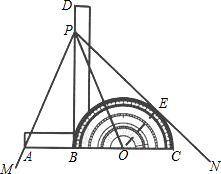 (2013•江东区模拟)数学家已证明“不能用直尺和圆规三等分角”.如果不限作图工具呢?有位数学爱好者制作了如下的“三等分角器”;将量角器直径BC和一条直尺AB放在同一条直线上,移动量角器使得AB=OB=OC,另一条直尺的边缘BD过点B,且BD⊥AB,并用固件按这样的位置固定.
(2013•江东区模拟)数学家已证明“不能用直尺和圆规三等分角”.如果不限作图工具呢?有位数学爱好者制作了如下的“三等分角器”;将量角器直径BC和一条直尺AB放在同一条直线上,移动量角器使得AB=OB=OC,另一条直尺的边缘BD过点B,且BD⊥AB,并用固件按这样的位置固定.
(1)如图,把∠MPN的顶点P放在三等分角器的BD线上,移动器具,使∠MPN的一边MP过点A,另一边PN和半圆相切.请你说明直线PB和PO三等分∠MON.
(2)若从量角器上读的∠COE=x(0<x<90°)请用含x的代数式表示∠MPN的度数. woor2171年前1
woor2171年前1 -
 小妖木木 共回答了15个问题
小妖木木 共回答了15个问题 |采纳率100%解题思路:(1)证Rt△PBO≌Rt△PEO,推出∠OPE=∠OPB,求出PA=PO,根据等腰三角形性质求出∠MPB=∠OPB,即可得出答案;
(2)根据全等推出∠POB=∠POE,求出∠POE=[1/2](180°-x)=90°-[1/2]x,根据三角形内角和定理求出∠MPO=[1/2]x,代入∠MPN=3∠MPO求出即可.(1)∵PN切⊙O于E,
∴PE⊥OE,
∵∠PBO=∠PEO=90°,
在Rt△PBO和Rt△PEO中,
PO=PO
OB=OE,
∴Rt△PBO≌Rt△PEO(HL),
∴∠OPE=∠OPB,
∵AB=BO,PB⊥OA,
∴PA=PB,
∴∠MPB=∠OPB,
即∠MPB=∠OPB=∠NPO.
(2)∵Rt△PBO≌Rt△PEO,
∴∠POB=∠POE,
∵∠EOC=x,
∴∠POE=[1/2](180°-x)=90°-[1/2]x,
∵∠PEO=90°,
∴∠MPO=90°-(90°-[1/2]x)=[1/2]x,
∴∠MPN=3∠MPO=[3/2]x.点评:
本题考点: 切线的性质;全等三角形的判定与性质.
考点点评: 本题考查了全等三角形的性质和判定,等腰三角形性质,线段垂直平分线性质,切线的性质的应用,主要考查学生综合运用性质进行推理的能力.1年前查看全部
- 如图,BE和BF三等分角ABC,CE和CF三等分角ACB,角A等于75°,求角BEC和BFC的度数.
 sileme1年前1
sileme1年前1 -
 guiwin 共回答了15个问题
guiwin 共回答了15个问题 |采纳率80%BFC 145度 BEC110度 步骤是 由题可以知道ABC 和ACB一共是105度,因为都是平分的,所以FBC和FCB加起来就是35度,BFC就是145度,另外步骤都是一样,EBC和ECB加起来就是70度,多以E就是110.1年前查看全部
- “三等分角”是数学史上一个著名的问题,但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给出的一种“三等分锐角”的
“三等分角”是数学史上一个著名的问题,但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法(如图):将给定的锐角∠AOB置于直角坐标系中,边OB在x轴上、边OA与函数y=[1/x]的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=[1/3]∠AOB.要明白帕普斯的方法,请研究以下问题:
(1)设P(a,[1/a])、R(b,[1/b]),求直线OM对应的函数表达式(用含a,b的代数式表示);
(2)分别过点P和R作y轴和x轴的平行线,两直线相交于点Q.请说明Q点在直线OM上,并据此证明 ∠MOB=[1/3]∠AOB;
∠MOB=[1/3]∠AOB;
(3)应用上述方法得到的结论,你如何三等分一个钝角(用文字简要说明). 宇宙351年前1
宇宙351年前1 -
 海南医学院食堂 共回答了13个问题
海南医学院食堂 共回答了13个问题 |采纳率100%解题思路:(1)直线OM是正比例函数,可利用所给的坐标得到M的坐标,代入函数解析式即可;
(2)根据所给的点的坐标得到Q的坐标,看是否符合(1)中的函数解析式;运用矩形的性质,作图过程中的条件,外角与不相邻内角的关系,即可得证;
(3)既然能作出锐角的三等分角,先将此钝角的一半(锐角)三等分,再作钝角的三等分角.(1)设直线OM的函数关系式为y=kx,P(a,[1/a])、R(b,[1/b]).(1分)
则M(b,[1/a]),
∴k=[1/a]÷b=[1/ab].(2分)
∴直线OM的函数关系式为y=[1/ab]x.(3分)
(2)∵Q的坐标(a,[1/b]),满足y=[1/ab]x,
∴点Q在直线OM上.
∵四边形PQRM是矩形,
∴SP=SQ=SR=SM=[1/2]PR.
∴∠SQR=∠SRQ.(5分)
∵PR=2OP,
∴PS=OP=[1/2]PR.
∴∠POS=∠PSO.(6分)
∵∠PSQ是△SQR的一个外角,
∴∠PSQ=2∠SQR.
∴∠POS=2∠SQR.(7分)
∵QR∥OB,
∴∠MOB=∠SQR.(8分)
∴∠POS=2∠MOB.(9分)
∴∠MOB=[1/3]∠AOB.(10分)
(3)①先做出钝角的一半,按照上述方法先将此钝角的一半(锐角)三等分,进而做出再做一个角与已做得的角相等即可得到钝角的三等分角.
②先作钝角的邻补角的三等分角,然后再以得到的三等分角作等边三角形可得钝角的三等分角,在钝角内作做出这个角即可.点评:
本题考点: 反比例函数综合题;作图—复杂作图.
考点点评: 过某个点,这个点的坐标应适合这个函数解析式.注意使用作图过程中利用的条件.1年前查看全部
- 三等分角问题证明。。!快!三等分角”是数学史上一个著名的问题,但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给
三等分角问题证明。。!快!
三等分角”是数学史上一个著名的问题,但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法(如图):将给定的锐角∠AOB置于直角坐标系中,边OB在x轴上、边OA与函数y=1/x 的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作 x轴和 y轴的平行线,两直线相交于点M ,连接OM得到∠MOB,则∠MOB= 1/3∠AOB.要明白帕普斯的方法,请研究以下问题:(1)设 P(a,1/a)、R(b,1/b) ,求直线OM对应的函数表达式(用含a,b 的代数式表示).
(2)分别过点P和R作 y轴和 x轴的平行线,两直线相交于点Q.请说明Q点在直线OM上,并据此证明∠MOB=1/3 ∠AOB.
 ccj78411年前2
ccj78411年前2 -
 youyoumake 共回答了16个问题
youyoumake 共回答了16个问题 |采纳率93.8%1年前查看全部
- 用尺规做图法能三等分角吗?很多人说他们自己想出来了等分的方法,它们的方法可行不?为什么?
 redapple731年前1
redapple731年前1 -
 xiankl198198 共回答了26个问题
xiankl198198 共回答了26个问题 |采纳率92.3%已证明,在尺规作图的前提下,此题无解.1年前查看全部
- 假设用有刻度的尺子和圆规,三等分角怎么分?好像阿基米德好像解出来了,
假设用有刻度的尺子和圆规,三等分角怎么分?好像阿基米德好像解出来了,
就是给你任意一个角,要你用有刻度的直尺和圆规把它三等分! bosun20081年前2
bosun20081年前2 -
 rqmildog 共回答了18个问题
rqmildog 共回答了18个问题 |采纳率88.9%首先以这个待等分的角的顶点为圆心,在不改变直径的情况下用圆规在角的两个边上各做一个标记,再用刻度尺把这两个标记和角的边的交叉点之间的距离3等分并做标记,再把顶点和最后做的两个标记连线,任务就完成了.1年前查看全部
- 求解一道三角形的证明题.任意三角形的三个角的三等分角平分线相交后构成的三角形DEF,证明DEF是等边三角形.
求解一道三角形的证明题.
 任意三角形的三个角的三等分角平分线相交后构成的三角形DEF,证明DEF是等边三角形.
任意三角形的三个角的三等分角平分线相交后构成的三角形DEF,证明DEF是等边三角形.  gefskk1年前2
gefskk1年前2 -
 gmg-fly 共回答了17个问题
gmg-fly 共回答了17个问题 |采纳率82.4%莫利定理,初等纯几何不容易,倒是正弦定理还是可以证明的1年前查看全部
- 在三角形ABC中,BE、BP三等分角ABC,CE,CP三等分角ACB,求角BPE
 鸿雁在云ldsllll1年前1
鸿雁在云ldsllll1年前1 -
 sdch 共回答了10个问题
sdch 共回答了10个问题 |采纳率90%证明:(1)∵∠ACB=90°
CD,CE三等分∠ACB ∠1∠2∠3就是三等分的那三个角
∴∠1=∠2=∠3=30°
∵CD⊥AB
∴∠A=30°
在Rt△ACB中
∵∠A=30°
∴AB=2BC
(2)∵∠BCE=60°,∠B=60°
∴△BCE为等边三角形
∴CE=EB
又∵∠1=30°,∠A=30°
∴CE=AE
∴CE=AE=EB1年前查看全部
- (2005•佛山)“三等分角”是数学史上一个著名的问题,但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给出的一
(2005•佛山)“三等分角”是数学史上一个著名的问题,但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法(如图):将给定的锐角∠AOB置于直角坐标系中,边OB在x轴上、边OA与函数y=[1/x]的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=[1/3]∠AOB.要明白帕普斯的方法,请研究以下问题:
(1)设P(a,[1/a])、R(b,[1/b]),求直线OM对应的函数表达式(用含a,b的代数式表示);
(2)分别过点P和R作y轴和x轴的平行线,两直线相交于点Q.请说明Q点在直线OM上,并据此证明 ∠MOB=[1/3]∠AOB;
∠MOB=[1/3]∠AOB;
(3)应用上述方法得到的结论,你如何三等分一个钝角(用文字简要说明). 抢一1年前1
抢一1年前1 -
 liuchangyi 共回答了19个问题
liuchangyi 共回答了19个问题 |采纳率94.7%解题思路:(1)直线OM是正比例函数,可利用所给的坐标得到M的坐标,代入函数解析式即可;
(2)根据所给的点的坐标得到Q的坐标,看是否符合(1)中的函数解析式;运用矩形的性质,作图过程中的条件,外角与不相邻内角的关系,即可得证;
(3)既然能作出锐角的三等分角,先将此钝角的一半(锐角)三等分,再作钝角的三等分角.(1)设直线OM的函数关系式为y=kx,P(a,[1/a])、R(b,[1/b]).(1分)
则M(b,[1/a]),
∴k=[1/a]÷b=[1/ab].(2分)
∴直线OM的函数关系式为y=[1/ab]x.(3分)
(2)∵Q的坐标(a,[1/b]),满足y=[1/ab]x,
∴点Q在直线OM上.
∵四边形PQRM是矩形,
∴SP=SQ=SR=SM=[1/2]PR.
∴∠SQR=∠SRQ.(5分)
∵PR=2OP,
∴PS=OP=[1/2]PR.
∴∠POS=∠PSO.(6分)
∵∠PSQ是△SQR的一个外角,
∴∠PSQ=2∠SQR.
∴∠POS=2∠SQR.(7分)
∵QR∥OB,
∴∠MOB=∠SQR.(8分)
∴∠POS=2∠MOB.(9分)
∴∠MOB=[1/3]∠AOB.(10分)
(3)①先做出钝角的一半,按照上述方法先将此钝角的一半(锐角)三等分,进而做出再做一个角与已做得的角相等即可得到钝角的三等分角.
②先作钝角的邻补角的三等分角,然后再以得到的三等分角作等边三角形可得钝角的三等分角,在钝角内作做出这个角即可.点评:
本题考点: 反比例函数综合题;作图—复杂作图.
考点点评: 过某个点,这个点的坐标应适合这个函数解析式.注意使用作图过程中利用的条件.1年前查看全部
- 尺规作图能三等分角吗?
 若妍雨1年前2
若妍雨1年前2 -
 刻薄女子 共回答了22个问题
刻薄女子 共回答了22个问题 |采纳率86.4%严格的尺规作图不能三等分任意给定角,但可以三等分特殊的角(3度的三倍数角,如9度、90度、180度).如果直尺有两个固定的刻度,则可以三等分任意角.1年前查看全部
- 关于三等分角?已知某角AOB.1:以O为圆心,作OA=OB;2:连接AB;3:作∠AOB的角平分线,交AB于点O';4:
关于三等分角?
已知某角AOB.1:以O为圆心,作OA=OB;2:连接AB;3:作∠AOB的角平分线,交AB于点O';4:以O'为圆心,O'A长为半径,画圆;5:以O'A为半径,点A为圆心画弧,交画下的圆于H点;6:以O'A为半径,点B为圆心画弧,交画下的圆于I点;7:连接OI和OH,OI和OH即三等分角线.不是尺规不能吗? caolq11年前1
caolq11年前1 -
 都市的风雨 共回答了18个问题
都市的风雨 共回答了18个问题 |采纳率88.9%这个方法做出来的不是三等分角
假设∠AOB=a,∠AOI=∠AOH=x
运用余弦定理和正弦定理后(过程略,可以自己算下)
得出:
sinx=[sina+√3*(1-cosa)]/√(16+8√3*sina)
不妨令a=60°
sinx=√3/2√7≈0.327
而sin20°≈0.342
所以sinx≠sin20°
x≠20°
所以∠AOI不是∠AOB的三等分角
另外,如果令a=90°的话,sinx=1/2,x恰好等于30°,呵呵,很具有迷惑性啊~~1年前查看全部
- 已知AB垂直CD于O,OE三等分角BOC,OF四等分角BOD,求EOF的度数?四种情况
 rxqzsy1年前1
rxqzsy1年前1 -
 蜈蚣的泪 共回答了16个问题
蜈蚣的泪 共回答了16个问题 |采纳率87.5%OE两种情况,一种靠近AB,一种靠近CD;同理OF也是两种情况,一种靠近AB,一种靠近CD
组合一下,
OE靠近AB,角BOE等于90/3=30度,
对应OF两种情况,
靠近AB,角BOF等于90/4=22.5度,角EOF为52.5度,
靠近CD,角BOF等于90-90/4=90-22.5=67.5度,角EOF为97.5度
OE靠近CD,角BOE等于90-90/3=60度,
对应OF两种情况,
靠近AB,角BOF等于90/4=22.5度,角EOF为82.5度,
靠近CD,角BOF等于90-90/4=90-22.5=67.5度,角EOF为127.5度1年前查看全部
- (三等分角)能三等分任意角吗?如果能,请证明!如不能,能三等分某些特殊角吗?如30 60 90 180等等 感激不尽!9
(三等分角)
能三等分任意角吗?如果能,请证明!如不能,能三等分某些特殊角吗?如30 60 90 180等等 感激不尽!
90度和180度怎么三等分?请加以证明! loveyou_forever1年前0
loveyou_forever1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
大家在问
- 1在1-100这一百个数中能被9整除的数的和是多少?
- 2(2013•重庆)合金是建筑航空母舰的主体材料.
- 3My Chinese teacher 作文
- 4一年级数学100表示什么
- 5物理大神请进总感觉没那么简单13
- 6为什么这一题的答案不是与and后的时态一致用were being cut
- 7五年级my cat写一篇短文,不少于50单词
- 8为什么archx不是等于ln(x-根号(x²-1))?
- 9已知整数X满足不等式3X-4小于等于6X-2和不等式(三分之2x+1)-1小于(三分之x-1)并且满足方程
- 10乡愁的诗歌反映了诗人怎样得情感和愿望
- 11列不等式解应用题:某次数学竞赛中共出了10道题,每答对1题得5分,每答错1题扣3分.若答题只有对错之分,问至少要答对几道
- 12一个棱长为1.5米的正方体铁皮盒子[无盖].至少需要多少平方米的铁皮?
- 13cannot convert from 'const class Line' to 'class Line
- 14蝉很爱叫怎么写成拟人句?
- 15333×332332333-332×333333332.


