托勒密定理用向量怎么证?请回应!
 杞人叹天2022-10-04 11:39:541条回答
杞人叹天2022-10-04 11:39:541条回答
已提交,审核后显示!提交回复
共1条回复
 A013 共回答了18个问题
A013 共回答了18个问题 |采纳率88.9%- 用初中相似三角形知识很容易证,没有必要用到向量.向量一般是证垂直之类问题.
有个挺有用的公式:(AB,CD)+(BC,AD)+(CA,BD)=0
(这里AB CD之类都是向量,(AB,CD)是AB CD点乘或者说是内积)
证明比较简单,用些什么AC=AB+BC之类的东西捣一捣就完了.
用这个来证平面的托米勒定理就不难了,由于(AB,CD)=|AB||CD|cos(AB,CD)
用四点共圆的条件就可以把那些cos去掉(注意符号),就得到了题目的结论.
广义托勒密定理:凸四边形ABCD的两组对边乘积的和大于等于它的两条对角线的乘积.
在四边形ABCD中,连接AC,作角ABE=角ACD,角BAE=角CAD
则三角形ABE和三角形ACD相似
所以 BE/CD=AB/AC,即BE*AC=AB*CD (1)
又有比例式AB/AC=AE/AD
而角BAC=角DAE
所以三角形ABC和三角形AED相似.
BC/ED=AC/AD即ED*AC=BC*AD (2)
(1)+(2),得
AC(BE+ED)=AB*CE+AD*BC
又因为BE+ED>=BD
所以命题得证
当且仅当E点落在线段BD上时,等号成立,此时ABCD内接于圆. - 1年前
相关推荐
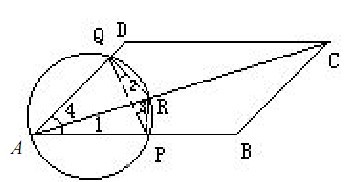
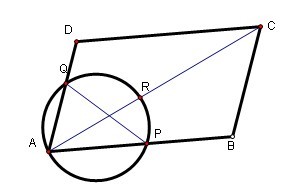
- 托勒密定理的应用如图,设P,Q为平行四边形ABCD的边AB,AD上的两点,三角形APQ的外接圆交对角线AC与R,求证:A
托勒密定理的应用
如图,设P,Q为平行四边形ABCD的边AB,AD上的两点,三角形APQ的外接圆交对角线AC与R,求证:AP.AB+AQ.AD=AR.AC
 绚烂de飞翔1年前1
绚烂de飞翔1年前1 -
 lyjq 共回答了20个问题
lyjq 共回答了20个问题 |采纳率85%1年前查看全部
- 四边形:托勒密定理及其推广三点共线与三线共点:梅涅劳斯定理塞瓦定理西姆松定理欧拉定理布里安香定理及其推广是什么?
 xueggsong1年前3
xueggsong1年前3 -
 007___12345 共回答了13个问题
007___12345 共回答了13个问题 |采纳率92.3%托勒密(Ptolemy)定理指出,圆内接凸四边形两对对边乘积的和等于两条对角线的乘积.
在直线上,托勒密定理同样成立,这时也称为欧拉定理.
托勒密定理的逆定理同样成立:一个凸四边形两对对边乘积的和等于两条对角线的乘积,则这个凸四边形内接于一圆.
推广及证明
* 托勒密不等式:四边形的任两组对边乘积不小于另外一组对边的乘积,取等号当且仅当共圆或共线.
o 简单的证明:复数恒等式:(a-b)(c-d)+(a-d)(b-c)=(a-c)(b-d),两边取模,得不等式,分析等号成立的条件.
o 四点不限于同一平面.
梅涅劳斯(Menelaus)定理(简称梅氏定理)是由古希腊数学家梅涅劳斯首先证明的.它指出:如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么(AF/FB)×(BD/DC)×(CE/EA)=1.或:设X、Y、Z分别在△ABC的BC、CA、AB所在直线上,则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=1 .
塞瓦定理 在△ABC内任取一点O,直线AO、BO、CO分别交对边于D、E、F,则 (BD/DC)*(CE/EA)*(AF/FB)=1
西姆松定理是一个几何定理.表述为:过三角形外接圆上异于三角形顶点的任意一点作三边的垂线,则三垂足共线.(此线常称为西姆松线).西姆松定理的逆定理为:若一点在三角形三边所在直线上的射影共线,则该点在此三角形的外接圆上.
在数论中,欧拉定理(也称费马-欧拉定理)是一个关于同余的性质.欧拉定理表明,若n,a为正整数,且n,a互素,(a,n) = 1,则 a^φ(n) ≡ 1 (mod n)
布里安香定理:圆的外切六边形的三条对角线共点.1年前查看全部
- 托勒密定理的证明过程有?2在任意四边形ABCD中,作△ABE使∠BAE=∠CAD ∠ABE=∠ ACD 因为△ABE∽△
托勒密定理的证明过程有?2
在任意四边形ABCD中,作△ABE使∠BAE=∠CAD ∠ABE=∠ ACD 因为△ABE∽△ACD 所以 BE/CD=AB/AC,即BE·AC=AB·CD (1) 而∠BAC=∠DAE,∠ACB=∠ADE 所以△ABC∽△AED相似.BC/ED=AC/AD即ED·AC=BC·AD (2) (1)+(2),得 AC(BE+ED)=AB·CD+AD·BC 又因为BE+ED≥BD (仅在四边形ABCD是某圆的内接四边形时,等号成立,即“托勒密定理”) 所以命题得证
以上来自百科.其中,∠ACB=∠ADE 是为什么? Flying-kiss1年前1
Flying-kiss1年前1 -
 tonyzhang_2005 共回答了21个问题
tonyzhang_2005 共回答了21个问题 |采纳率85.7%在证明此对三角形相似前应该无法知道∠ACB=∠ADE.
但有△ABE∽△ACD则AB/AC=AE/AD
故AB/AE=AC/AD(比例转换)
又由∠BAE=∠CAD知∠BAC=∠EAD;
由此可得△ABC∽△AED,还是可以得到最后的结论.
这对相似应该就是这么证的,百科那位很可能是默认四点共圆直接得出的两角相等...
如果非想证∠ACB=∠ADE的话就用正弦定理,但结果是一样的.1年前查看全部
- 托勒密定理怎么证?
 天竺教父1年前2
天竺教父1年前2 -
 4802647 共回答了20个问题
4802647 共回答了20个问题 |采纳率85%托勒密定理:圆内接四边形中,两条对角线的乘积等于两组对边乘积之和
已知:圆内接四边形ABCD,求证:AC•BD=AB•CD+AD•BC
字数限制1年前查看全部
- 我需要那种能省很多字数的公式定理,且可以直接用的那种,像托勒密定理
 zky_zky1年前6
zky_zky1年前6 -
 b5t5i 共回答了18个问题
b5t5i 共回答了18个问题 |采纳率83.3%初中数学所有公式
1、 每份数×份数=总数 总数÷每份数=份数总数÷份数=每份数
2、 1倍数×倍数=几倍数 几倍数÷1倍数=倍数几倍数÷倍数=1倍数
3、 速度×时间=路程 路程÷速度=时间 路程÷时间=速度
4、 单价×数量=总价 总价÷单价=数量 总价÷数量=单价
5、 工作效率×工作时间=工作总量 工作总量÷工作效率=工作时间工作总量÷
工作时间=工作效率
6、 加数+加数=和 和-一个加数=另一个加数
7、 被减数-减数=差 被减数-差=减数 差+减数=被减数
8、 因数×因数=积 积÷一个因数=另一个因数
9、 被除数÷除数=商 被除数÷商=除数 商×除数=被除数
小学数学图形计算公式
1、正方形:C周长 S面积 a边长 周长=边长×4, C=4a 面积=边长×边长, S=a×a
2、正方体:V:体积 a:棱长 表面积=棱长×棱长×6 , S表=a×a×6
体积=棱长×棱长×棱长 ,V=a×a×a
3、长方形
C周长 S面积 a边长 周长=(长+宽)×2 ,C=2(a+b) 面积=长×宽 , S=ab
4、长方体
V:体积 s:面积 a:长 b: 宽 h:高
(1)表面积(长×宽+长×高+宽×高)×2 , S=2(ab+ah+bh)
(2)体积=长×宽×高 , V=abh
5、三角形
s面积 a底 h高 面积=底×高÷2 s=ah÷2
三角形高=面积 ×2÷底
三角形底=面积 ×2÷高
6、平行四边形:s面积 a底 h高 面积=底×高 s=ah
7、梯形:s面积 a上底 b下底 h高 面积=(上底+下底)×高÷2 s=(a+b)× h÷2
8 圆形:S面积 C周长 ∏ d=直径 r=半径
(1)周长=直径×∏=2×∏×半径 , C=∏d=2∏r
(2)面积=半径×半径×∏
9、圆柱体:v体积 h:高 s底面积 r底面半径 c底面周长
(1)侧面积=底面周长×高
(2)表面积=侧面积+底面积×2
(3)体积=底面积×高
(4)体积=侧面积÷2×半径
10、圆锥体:v体积 h高 s底面积 r底面半径 体积=底面积×高÷3
植树问题
1、非封闭线路上的植树问题主要可分为以下三种情形:
⑴如果在非封闭线路的两端都要植树,那么:
株数=段数+1=全长÷株距-1
全长=株距×(株数-1)
株距=全长÷(株数-1)
⑵如果在非封闭线路的一端要植树,另一端不要植树,那么:
株数=段数=全长÷株距
全长=株距×株数
株距=全长÷株数
⑶如果在非封闭线路的两端都不要植树,那么:
株数=段数-1=全长÷株距-1
全长=株距×(株数+1)
株距=全长÷(株数+1)
2、封闭线路上的植树问题的数量关系如下
株数=段数=全长÷株距
全长=株距×株数
株距=全长÷株数
盈亏问题
(盈+亏)÷两次分配量之差=参加分配的份数
(大盈-小盈)÷两次分配量之差=参加分配的份数
(大亏-小亏)÷两次分配量之差=参加分配的份数
相遇问题
相遇路程=速度和×相遇时间
相遇时间=相遇路程÷速度和
速度和=相遇路程÷相遇时间
追及问题
追及距离=速度差×追及时间
追及时间=追及距离÷速度差
速度差=追及距离÷追及时间
流水问题
顺流速度=静水速度+水流速度
逆流速度=静水速度-水流速度
静水速度=(顺流速度+逆流速度)÷2
水流速度=(顺流速度-逆流速度)÷2
浓度问题
溶质的重量+溶剂的重量=溶液的重量
溶质的重量÷溶液的重量×100%=浓度
溶液的重量×浓度=溶质的重量
溶质的重量÷浓度=溶液的重量
利润与折扣问题
利润=售出价-成本
利润率=利润÷成本×100%=(售出价÷成本-1)×100%
涨跌金额=本金×涨跌百分比
折扣=实际售价÷原售价×100%(折扣<1)
利息=本金×利率×时间
税后利息=本金×利率×时间×(1-20%)
长度单位换算
1千米=1000米 1米=10分米
1分米=10厘米 1米=100厘米
1厘米=10毫米
面积单位换算
1平方千米=100公顷
1公顷=10000平方米
1平方米=100平方分米
1平方分米=100平方厘米
1平方厘米=100平方毫米
体(容)积单位换算
1立方米=1000立方分米
1立方分米=1000立方厘米
1立方分米=1升
1立方厘米=1毫升
1立方米=1000升
重量单位换算
1吨=1000 千克
1千克=1000克
1千克=1公斤
人民币单位换算
1元=10角
1角=10分
1元=100分
时间单位换算
1世纪=100年 1年=12月
大月(31天)有:135781012月
小月(30天)的有:46911月
平年 2月28天, 闰年 2月29天
平年全年365天, 闰年全年366天
1日=24小时 1小时=60分
1分=60秒 1小时=3600秒
小学数学几何形体周长 面积 体积计算公式
1、长方形的周长=(长+宽)×2 C=(a+b)×2
2、正方形的周长=边长×4 C=4a
3、长方形的面积=长×宽 S=ab
4、正方形的面积=边长×边长 S=a.×a=a2
5、三角形的面积=底×高÷2 S=ah÷2
6、平行四边形的面积=底×高 S=ah
7、梯形的面积=(上底+下底)×高÷2 ,S=(a+b)h÷2
8、直径=半径×2 d=2r 半径=直径÷2 r= d÷2
9、圆的周长=圆周率×直径=圆周率×半径×2 c=πd =2πr
10、圆的面积=圆周率×半径×半径 =πr2
常见的初中数学公式
1 过两点有且只有一条直线
2 两点之间线段最短
3 同角或等角的补角相等
4 同角或等角的余角相等
5 过一点有且只有一条直线和已知直线垂直
6 直线外一点与直线上各点连接的所有线段中,垂线段最短
7 平行公理 经过直线外一点,有且只有一条直线与这条直线平行
8 如果两条直线都和第三条直线平行,这两条直线也互相平行
9 同位角相等,两直线平行
10 内错角相等,两直线平行
11 同旁内角互补,两直线平行
12 两直线平行,同位角相等
13 两直线平行,内错角相等
14 两直线平行,同旁内角互补
15 定理 三角形两边的和大于第三边
16 推论 三角形两边的差小于第三边
17 三角形内角和定理 三角形三个内角的和等于180°
18 推论1 直角三角形的两个锐角互余
19 推论2 三角形的一个外角等于和它不相邻的两个内角的和
20 推论3 三角形的一个外角大于任何一个和它不相邻的内角
21 全等三角形的对应边、对应角相等
22 边角边公理(SAS) 有两边和它们的夹角对应相等的两个三角形全等
23 角边角公理(ASA) 有两角和它们的夹边对应相等的两个三角形全等
24 推论(AAS) 有两角和其中一角的对边对应相等的两个三角形全等
25 边边边公理(SSS) 有三边对应相等的两个三角形全等
26 斜边、直角边公理(HL)有斜边和一条直角边对应相等的两个直角三角形全等
27 定理1 在角的平分线上的点到这个角的两边的距离相等
28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上
29 角的平分线是到角的两边距离相等的所有点的集合
30 等腰三角形的性质定理 等腰三角形的两个底角相等 (即等边对等角)
31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边
32 等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合
33 推论3 等边三角形的各角都相等,并且每一个角都等于60°
34 等腰三角形的判定定理 如果一个三角形有两个角相等,那么这两个角所对
的边也相等(等角对等边)
35 推论1 三个角都相等的三角形是等边三角形
36 推论2 有一个角等于60°的等腰三角形是等边三角形
37 在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半
38 直角三角形斜边上的中线等于斜边上的一半
39 定理 线段垂直平分线上的点和这条线段两个端点的距离相等
40 逆定理 和一条线段两个端点距离相等的点,在这条线段的垂直平分线上
41 线段的垂直平分线可看作和线段两端点距离相等的所有点的集合
42 定理 1 关于某条直线对称的两个图形是全等形
43 定理 2 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平
分线
44 定理 3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那
么交点在对称轴上
45 逆定理 如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图
形关于这条直线对称
46 勾股定理 直角三角形两直角边a、b的平方和、等于斜边c的平方,
即a2+b2=c2
47 勾股定理的逆定理 如果三角形的三边长a、b、c有a2+b2=c2关系,那
么这个三角形是直角三角形
48 定理 四边形的内角和等于360°
49 四边形的外角和等于360°
50 多边形内角和定理 n边形的内角的和等于(n-2)×180°
51 推论 任意多边的外角和等于360°
52 平行四边形性质定理 1 平行四边形的对角相等
53 平行四边形性质定理 2 平行四边形的对边相等
54 推论 夹在两条平行线间的平行线段相等
55 平行四边形性质定理 3 平行四边形的对角线互相平分
56 平行四边形判定定理 1 两组对角分别相等的四边形是平行四边形
57 平行四边形判定定理 2 两组对边分别相等的四边形是平行四边形
58 平行四边形判定定理 3 对角线互相平分的四边形是平行四边形
59 平行四边形判定定理 4 一组对边平行相等的四边形是平行四边形
60 矩形性质定理 1 矩形的四个角都是直角
61 矩形性质定理 2 矩形的对角线相等
62 矩形判定定理 1 有三个角是直角的四边形是矩形
63 矩形判定定理 2 对角线相等的平行四边形是矩形
64 菱形性质定理 1 菱形的四条边都相等
65 菱形性质定理 2 菱形的对角线互相垂直,并且每一条对角线平分一组对角
66 菱形面积=对角线乘积的一半,即S=(a×b)÷2
67 菱形判定定理 1 四边都相等的四边形是菱形
68 菱形判定定理 2 对角线互相垂直的平行四边形是菱形
69 正方形性质定理 1 正方形的四个角都是直角,四条边都相等
70 正方形性质定理 2 正方形的两条对角线相等,并且互相垂直平分,每条对
角线平分一组对角
71 定理 1 关于中心对称的两个图形是全等的
72 定理 2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对
称中心平分
73 逆定理 如果两个图形的对应点连线都经过某一点,并且被这一点平分,那
么这两个图形关于这一点对称
74 等腰梯形性质定理 等腰梯形在同一底上的两个角相等
75 等腰梯形的两条对角线相等
76 等腰梯形判定定理 在同一底上的两个角相等的梯形是等腰梯形
77 对角线相等的梯形是等腰梯形
78 平行线等分线段定理 如果一组平行线在一条直线上截得的线段相等,那么
在其他直线上截得的线段也相等
79 推论 1 经过梯形一腰的中点与底平行的直线,必平分另一腰
80 推论 2 经过三角形一边的中点与另一边平行的直线,必平分第三边
81 三角形中位线定理 三角形的中位线平行于第三边,并且等于它的一半
82 梯形中位线定理 梯形的中位线平行于两底,并且等于两底和的一半
L=(a+b)÷2 , S=L×h
83 (1)比例的基本性质 如果a:b=c:d,那么ad=bc如果ad=bc,那么a:b=c:d
84 (2)合比性质 如果a/b=c/d,那么(a±b)/b=(c±d)/d
85 (3)等比性质 如果a/b=c/d=…=m/n(b+d+…+n≠0),那么(a+c+…+m)/
(b+d+…+n)=a/b
86 平行线分线段成比例定理 三条平行线截两条直线,所得的对应线段成比例
87 推论 平行于三角形一边的直线截其他两边(或两边的延长线),所得的对
应线段成比例
88 定理 如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成
比例,那么这条直线平行于三角形的第三边
89 平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边
与原三角形三边对应成比例
90 定理 平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构
成的三角形与原三角形相似
91 相似三角形判定定理 1 两角对应相等,两三角形相似(ASA)
92 直角三角形被斜边上的高分成的两个直角三角形和原三角形相似
93 判定定理 2 两边对应成比例且夹角相等,两三角形相似(SAS)
94 判定定理 3 三边对应成比例,两三角形相似(SSS)
95 定理 如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边
和一条直角边对应成比例,那么这两个直角三角形相似
96 性质定理 1 相似三角形对应高的比,对应中线的比与对应角平分线的比都
等于相似比
97 性质定理 2 相似三角形周长的比等于相似比
98 性质定理 3 相似三角形面积的比等于相似比的平方
99 任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角
的正弦值
100 任意锐角的正切值等于它的余角的余切值,任意锐角的余切值等于它的余角
的正切值
101 圆是定点的距离等于定长的点的集合
102 圆的内部可以看作是圆心的距离小于半径的点的集合
103 圆的外部可以看作是圆心的距离大于半径的点的集合
104 同圆或等圆的半径相等
105 到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半径的圆
106 和已知线段两个端点的距离相等的点的轨迹,是着条线段的垂直平分线
107 到已知角的两边距离相等的点的轨迹,是这个角的平分线
108 到两条平行线距离相等的点的轨迹,是和这两条平行线平行且距离相等的一
条直线
109 定理 不在同一直线上的三点确定一个圆.
110 垂径定理 垂直于弦的直径平分这条弦并且平分弦所对的两条弧
111 推论 1
①平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧
②弦的垂直平分线经过圆心,并且平分弦所对的两条弧
③平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧
112 推论2 圆的两条平行弦所夹的弧相等
113 圆是以圆心为对称中心的中心对称图形
114 定理 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对
的弦的弦心距相等
115 推论 在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两弦的弦心距
中有一组量相等那么它们所对应的其余各组量都相等
116 定理 一条弧所对的圆周角等于它所对的圆心角的一半
117 推论 1 同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对
的弧也相等
118 推论 2 半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径
119 推论 3 如果三角形一边上的中线等于这边的一半,那么这个三角形是直角
三角形
120 定理 圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角
121 ①直线L和⊙O相交 d<r
②直线L和⊙O相切 d=r
③直线L和⊙O相离 d>r
122 切线的判定定理 经过半径的外端并且垂直于这条半径的直线是圆的切线
123 切线的性质定理 圆的切线垂直于经过切点的半径
124 推论 1 经过圆心且垂直于切线的直线必经过切点
125 推论 2 经过切点且垂直于切线的直线必经过圆心
126 切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一
点的连线平分两条切线的夹角
127 圆的外切四边形的两组对边的和相等
128 弦切角定理 弦切角等于它所夹的弧对的圆周角
129 推论 如果两个弦切角所夹的弧相等,那么这两个弦切角也相等
130 相交弦定理 圆内的两条相交弦,被交点分成的两条线段长的积相等
131 推论 如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的
比例中项
132 切割线定理 从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点
的两条线段长的比例中项
133 推论 从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线
段长的积相等
134 如果两个圆相切,那么切点一定在连心线上
135 ①两圆外离 d>R+r ②两圆外切 d=R+r
③两圆相交 R-r<d<R+r(R>r)
④两圆内切 d=R-r(R>r) ⑤两圆内含d<R-r(R>r)
136 定理 相交两圆的连心线垂直平分两圆的公共弦
137 定理 把圆分成n(n≥3):
⑴依次连结各分点所得的多边形是这个圆的内接正n边形
⑵经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外
切正n边形
138 定理 任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆
139 正n边形的每个内角都等于(n-2)×180°/n
140 定理 正n边形的半径和边心距把正n边形分成2n个全等的直角三角形
141 正n边形的面积Sn=pnrn/2 p表示正n边形的周长
142 正三角形面积√3a/4 a表示边长
143 如果在一个顶点周围有k个正n边形的角,由于这些角的和应为360°,
因此k×(n-2)180°/n=360°化为(n-2)(k-2)=4
144 弧长计算公式:L=n兀R/180
145 扇形面积公式:S扇形=n兀R^2/360=LR/2
146 内公切线长= d-(R-r) 外公切线长= d-(R+r)
乘法与因式分解 a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2)
a3-b3=(a-b)(a2+ab+b2)
三角不等式 |a+b|≤|a|+|b| |a-b|≤|a|+|b| |a|≤b-b≤a≤b
|a-b|≥|a|-|b| -|a|≤a≤|a|
一元二次方程的解 -b+√(b2-4ac)/2a, -b-√(b2-4ac)/2a
根与系数的关系 X1+X2=-b/a X1*X2=c/a 注:韦达定理
判别式
b2-4ac=0 注:方程有两个相等的实根
b2-4ac>0 注:方程有两个不等的实根
b2-4ac0
抛物线标准方程 y2=2px y2=-2px x2=2py x2=-2py
直棱柱侧面积 S=c*h 斜棱柱侧面积 S=c'*h
正棱锥侧面积 S=1/2c*h' 正棱台侧面积 S=1/2(c+c')h'
圆台侧面积 S=1/2(c+c')l=pi(R+r)l 球的表面积 S=4pi*r2
圆柱侧面积 S=c*h=2pi*h 圆锥侧面积 S=1/2*c*l=pi*r*l
弧长公式 l=a*r a是圆心角的弧度数r >0 扇形面积公式 s=1/2*l*r
锥体体积公式 V=1/3*S*H 圆锥体体积公式 V=1/3*pi*r2h
斜棱柱体积 V=S'L 注:其中,S'是直截面面积, L是侧棱长
柱体体积公式 V=s*h 圆柱体 V=pi*r2h1年前查看全部
- 利用西姆松定理证明托勒密定理.(提示:本题要使用正弦定理
 年韩吕1年前1
年韩吕1年前1 -
 tea_leaf3 共回答了27个问题
tea_leaf3 共回答了27个问题 |采纳率85.2%证明
在四边形ABCD中,连接AC,作角ABE=角ACD,角BAE=角CAD
则三角形ABE和三角形ACD相似
所以 BE/CD=AB/AC,即BE*AC=AB*CD (1)
又有比例式AB/AC=AE/AD
而角BAC=角DAE
所以三角形ABC和三角形AED相似.
BC/ED=AC/AD即ED*AC=BC*AD (2)
(1)+(2),得
AC(BE+ED)=AB*CD+AD*BC
又因为BE+ED>=BD
所以命题得证
推论
任意凸四边形ABCD,必有AC·BD≤AB·CD+AD·BC,当且仅当ABCD四点共圆时取等号.
托勒密定理的逆定理同样成立:一个凸四边形两对对边乘积的和等于两条对角线的乘积,则这个凸四边形内接于一圆1年前查看全部
- 托勒密定理、西姆松定理.如何证明托勒密定理不等式、西姆松定理.配下图方便理解
 fgood1年前1
fgood1年前1 -
 dcstas 共回答了18个问题
dcstas 共回答了18个问题 |采纳率83.3%证明
在四边形ABCD中,连接AC,作角ABE=角ACD,角BAE=角CAD
则三角形ABE和三角形ACD相似
所以 BE/CD=AB/AC,即BE*AC=AB*CD (1)
又有比例式AB/AC=AE/AD
而角BAC=角DAE
所以三角形ABC和三角形AED相似.
BC/ED=AC/AD即ED*AC=BC*AD (2)
(1)+(2),得
AC(BE+ED)=AB*CD+AD*BC
又因为BE+ED>=BD
所以命题得证
推论
任意凸四边形ABCD,必有AC·BD≤AB·CD+AD·BC,当且仅当ABCD四点共圆时取等号.
托勒密定理的逆定理同样成立:一个凸四边形两对对边乘积的和等于两条对角线的乘积,则这个凸四边形内接于一圆
推广
托勒密不等式:四边形的任两组对边乘积不小于另外一组对边的乘积,取等号当且仅当共圆或共线.
简单的证明:复数恒等式:(a-b)(c-d)+(a-d)(b-c)=(a-c)(b-d),两边取模,得不等式,分析等号成立的条件.
四点不限于同一平面.
在一条线段上AD上,顺次标有B、C两点,则AD*BC+AB*CD=AC*BD
从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上.
证明:
△ABC外接圆上有点P,且PE⊥AC于E,PF⊥AB于F,PD⊥BC于D,分别连DE、DF.
易证P、B、F、D及P、D、C、E和A、B、P、C分别共圆,于是∠FDP=∠ACP ①,(∵都是∠ABP的补角) 且∠PDE=∠PCE
② 而∠ACP+∠PCE=180°
③ ∴∠FDP+∠PDE=180°
④ 即F、D、E共线. 反之,当F、D、E共线时,由④→②→③→①可见A、B、P、E共圆.1年前查看全部
- 给出托勒密定理的逆定理的证明过程,
 三级女郎1年前1
三级女郎1年前1 -
 4s4l 共回答了11个问题
4s4l 共回答了11个问题 |采纳率90.9%1年前查看全部
- 几个重要定理的内熔:梅涅劳斯定理、塞瓦定理、托勒密定理、西姆松定理.
几个重要定理的内熔:梅涅劳斯定理、塞瓦定理、托勒密定理、西姆松定理.
有什么例题麽 liwentao4441年前2
liwentao4441年前2 -
 methinks 共回答了22个问题
methinks 共回答了22个问题 |采纳率90.9%塞瓦定理 塞瓦定理 开放分类: 数学、三角形、定理 塞瓦定理 设O是△ABC内任意一点, AO、BO、CO分别交对边于D、E、F,则 (BD/DC)*(CE/EA)*(AF/FB)=1 证法简介 (Ⅰ)本题可利用梅涅劳斯定理证明: ∵△ADC被直线BOE所截, ∴ (CB/BD)*(DO/OA)*(AE/EC)=1 ① 而由△ABD被直线COF所截,∴ (BC/CD)*(DO/OA)*(AF/BF)=1② ②÷①:即得:(BD/DC)*(CE/EA)*(AF/FB)=1 (Ⅱ)也可以利用面积关系证明 ∵BD/DC=S△ABD/S△ACD=S△BOD/S△COD=(S△ABD-S△BOD)/(S△ACD-S△COD)=S△AOB/S△AOC ③ 同理CE/EA=S△BOC/ S△AOB ④ AF/FB=S△AOC/S△BOC ⑤ ③×④×⑤得BD/DC*CE/EA*AF/FB=1 利用塞瓦定理证明三角形三条高线必交于一点: 设三边AB、BC、AC的垂足分别为D、E、F, 根据塞瓦定理逆定理,因为(AD:DB)*(BE:EC)*(CF:FA)=[(CD*ctgA)/[(CD*ctgB)]*[(AE*ctgB)/(AE*ctgC)]*[(BF*ctgC)/ [(AE*ctgB)]=1,所以三条高CD、AE、BF交于一点. 托勒密定理 定理的提出 [编辑本段] 一般几何教科书中的“托勒密定理”,实出自依巴谷(Hipparchus)之手,托勒密只是从他的书中摘出. 定理的内容 [编辑本段] 托勒密(Ptolemy)定理指出,圆内接凸四边形两对对边乘积的和等于两条对角线的乘积. 原文:圆内接四边形中,两对角线所包矩形的面积等于 一组对边所包矩形的面积与另一组对边所包矩形的面积之和. 从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质. 证明 [编辑本段] (以下是推论的证明,托勒密定理可视作特殊情况.) 在任意四边形ABCD中,连接AC,作∠BAE=∠CAD,因为∠ABE=∠ACD 则△ABE∽△ACD 所以BE/CD=AB/AC,即BE·AC=AB·CD (1) 又有比例式AB/AC=AE/AD 而∠BAC=∠DAE 所以△ABC∽△AED相似. BC/ED=AC/AD即ED·AC=BC·AD (2) (1)+(2),得 AC(BE+ED)=AB·CD+AD·BC 又因为BE+ED≥BD (仅在四边形ABCD是某圆的内接四边形时,等号成立,即“托勒密定理”) 所以命题得证 推论 [编辑本段] 1.任意凸四边形ABCD,必有AC·BD≤AB·CD+AD·BC,当且仅当ABCD四点共圆时取等号. 2.托勒密定理的逆定理同样成立:一个凸四边形两对对边乘积的和等于两条对角线的乘积,则这个凸四边形内接于一圆、 推广 [编辑本段] 托勒密不等式:四边形的任两组对边乘积不小于另外一组对边的乘积,取等号当且仅当共圆或共线. 简单的证明:复数恒等式:(a-b)(c-d)+(a-d)(b-c)=(a-c)(b-d),两边取模, 得不等式AC·BD≤|(a-b)(c-d)|+|(b-c)(a-d)|=AB·CD+BC·AD 注意: 1.等号成立的条件是(a-b)(c-d)与(a-d)(b-c)的辐角相等,这与A、B、C、D四点共圆等价. 2.四点不限于同一平面. 欧拉定理:在一条线段上AD上,顺次标有B、C两点,则AD·BC+AB·CD=AC·BD
满意请采纳1年前查看全部
- 关于复数的模和托勒密定理用a、b、c、d分别表示四边形顶点A、B、C、D的复数,则AB、CD、AD、BC、AC、BD的长
关于复数的模和托勒密定理
用a、b、c、d分别表示四边形顶点A、B、C、D的复数,则AB、CD、AD、BC、AC、BD的长度分别是:(a-b)、(c-d)、(a-d)、(b-c)、(a-c)、(b-d).首先注意到复数恒等式:(a − b)(c − d) + (a − d)(b − c) = (a − c)(b − d) ,两边取模,运用三角不等式得.等号成立的条件是(a-b)(c-d)与(a-d)(b-c)的辐角相等,这与A、B、C、D四点共圆等价.
(a − b)(c − d) + (a − d)(b − c) = (a − c)(b − d) ,两边取模,然后得到什么?怎么看不懂呢?
为什么∣(a-b)(c-d)∣就能表示为两边之积呢?不是两向量之积德模吗? wkb171341www1年前1
wkb171341www1年前1 -
 空山月影 共回答了25个问题
空山月影 共回答了25个问题 |采纳率92%∣(a-c)(b-d)∣=∣(a-b)*(c-d)+(a-d)*(b-c)∣≤∣(a-b)(c-d)∣+∣(a-d)(b-d)∣
这个是简单的实数不等式
下面会了吧
把每一个小括号里复数对应到边长,因为绝对值里面只有乘法了,所以可以如此对应
证毕
求个最佳,即采纳1年前查看全部
- 怎样证明托勒密定理?
 一场路过1年前1
一场路过1年前1 -
 for110 共回答了22个问题
for110 共回答了22个问题 |采纳率90.9%在任意凸四边形ABCD中,作△ABE使∠BAE=∠CAD ∠ABE=∠ ACD,连接DE.
则△ABE∽△ACD
所以 BE/CD=AB/AC,即BE·AC=AB·CD (1) 由△ABE∽△ACD得AD/AC=AE/AB,又∠BAC=∠EAD,
所以△ABC∽△AED.
BC/ED=AC/AD,即ED·AC=BC·AD (2)
(1)+(2),得
AC(BE+ED)=AB·CD+AD·BC
又因为BE+ED≥BD
(仅在四边形ABCD是某圆的内接四边形时,等号成立,即“托勒密定理”)1年前查看全部
- 数学和科学的.类似托勒密定理
 xlshane1年前1
xlshane1年前1 -
 轻轻地飘去 共回答了16个问题
轻轻地飘去 共回答了16个问题 |采纳率81.3%大于0的数叫正数,前面加上负号的数叫负数 0既不是负数也不是正数
整数可以看作分母为1的分数.正整数,0’负整数’正分数,负分数 写成分数的形式称为有理数. 在直线上任取一个点表示数0,这个点叫做原点
只有负号不同的两个数叫做互为相反数一般的,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作IaI 一个正数的绝对值是它的本身;一个负数的绝对值是它的相反数;0的绝对值是0 (1)正数大于0,0大于负数,正数大于负数; (2)两个负数,绝对值大的反而小.
有理数加法法则:1.同号相加,取相同负号.并把绝对值相加 2.绝对值不相等的异号两数相加,取绝对值较大的加数的负号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0. 3.一个数同0相加,仍得这个数
有理数减法法则:减去一个数,等于加上这个数的相反数
有理数乘法法则:两数相乘,同号得正,负号得负,并把绝对值相乘. 任何数同0相乘都得0
有理数除发法则:除以一个不为0的数,等于乘以这个数的相反数
都是数字或字母的积,叫做单项式 单独的一个数或一个字母也叫单项式 单项式中的数字因数叫做这个单项式的积 一个单项式中,所有字母的指数的和叫做这个单项式的次数. 几个单项式的和叫做多项式 其中每个单项式叫做多项式的项 不含字母的叫做常数项 多项式里次数最高项的次数,叫做这个多项式的次数
1.皮克公式 S=a+1/2b-1
2.等和数列之一: 5+6*(n-1)
几何公式和定理(初中)
1 过两点有且只有一条直线
2 两点之间线段最短
3 同角或等角的补角相等
4 同角或等角的余角相等
5 过一点有且只有一条直线和已知直线垂直
6 直线外一点与直线上各点连接的所有线段中,垂线段最短
7 平行公理 经过直线外一点,有且只有一条直线与这条直线平行
8 如果两条直线都和第三条直线平行,这两条直线也互相平行
9 同位角相等,两直线平行
10 内错角相等,两直线平行
11 同旁内角互补,两直线平行
12两直线平行,同位角相等
13 两直线平行,内错角相等
14 两直线平行,同旁内角互补
15 定理 三角形两边的和大于第三边
16 推论 三角形两边的差小于第三边
17 三角形内角和定理 三角形三个内角的和等于180°
18 推论1 直角三角形的两个锐角互余
19 推论2 三角形的一个外角等于和它不相邻的两个内角的和
20 推论3 三角形的一个外角大于任何一个和它不相邻的内角
21 全等三角形的对应边、对应角相等
22边角边公理(SAS) 有两边和它们的夹角对应相等的两个三角形全等
23 角边角公理( ASA)有两角和它们的夹边对应相等的两个三角形全等
24 推论(AAS) 有两角和其中一角的对边对应相等的两个三角形全等
25 边边边公理(SSS) 有三边对应相等的两个三角形全等
26 斜边、直角边公理(HL) 有斜边和一条直角边对应相等的两个直角三角形全等
27 定理1 在角的平分线上的点到这个角的两边的距离相等
28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上
29 角的平分线是到角的两边距离相等的所有点的集合
30 等腰三角形的性质定理 等腰三角形的两个底角相等 (即等边对等角)
31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边
32 等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合
33 推论3 等边三角形的各角都相等,并且每一个角都等于60°
34 等腰三角形的判定定理 如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)
35 推论1 三个角都相等的三角形是等边三角形
36 推论 2 有一个角等于60°的等腰三角形是等边三角形
37 在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半
38 直角三角形斜边上的中线等于斜边上的一半
39 定理 线段垂直平分线上的点和这条线段两个端点的距离相等
40 逆定理 和一条线段两个端点距离相等的点,在这条线段的垂直平分线上
41 线段的垂直平分线可看作和线段两端点距离相等的所有点的集合
42 定理1 关于某条直线对称的两个图形是全等形
43 定理 2 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线
44定理3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上
45逆定理 如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称
46勾股定理 直角三角形两直角边a、b的平方和、等于斜边c的平方,即a^2+b^2=c^2
47勾股定理的逆定理 如果三角形的三边长a、b、c有关系a^2+b^2=c^2 ,那么这个三角形是直角三角形
48定理 四边形的内角和等于360°
49四边形的外角和等于360°
50多边形内角和定理 n边形的内角的和等于(n-2)×180°
51推论 任意多边的外角和等于360°
52平行四边形性质定理1 平行四边形的对角相等
53平行四边形性质定理2 平行四边形的对边相等
54推论 夹在两条平行线间的平行线段相等
55平行四边形性质定理3 平行四边形的对角线互相平分
56平行四边形判定定理1 两组对角分别相等的四边形是平行四边形
57平行四边形判定定理2 两组对边分别相等的四边形是平行四边形
58平行四边形判定定理3 对角线互相平分的四边形是平行四边形
59平行四边形判定定理4 一组对边平行相等的四边形是平行四边形
60矩形性质定理1 矩形的四个角都是直角
61矩形性质定理2 矩形的对角线相等
62矩形判定定理1 有三个角是直角的四边形是矩形
63矩形判定定理2 对角线相等的平行四边形是矩形
64菱形性质定理1 菱形的四条边都相等
65菱形性质定理2 菱形的对角线互相垂直,并且每一条对角线平分一组对角
66菱形面积=对角线乘积的一半,即S=(a×b)÷2
67菱形判定定理1 四边都相等的四边形是菱形
68菱形判定定理2 对角线互相垂直的平行四边形是菱形
69正方形性质定理1 正方形的四个角都是直角,四条边都相等
70正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角
71定理1 关于中心对称的两个图形是全等的
72定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分
73逆定理 如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称
74等腰梯形性质定理 等腰梯形在同一底上的两个角相等
75等腰梯形的两条对角线相等
76等腰梯形判定定理 在同一底上的两个角相等的梯形是等腰梯形
77对角线相等的梯形是等腰梯形
78平行线等分线段定理 如果一组平行线在一条直线上截得的线段
相等,那么在其他直线上截得的线段也相等
79 推论1 经过梯形一腰的中点与底平行的直线,必平分另一腰
80 推论2 经过三角形一边的中点与另一边平行的直线,必平分第
三边
81 三角形中位线定理 三角形的中位线平行于第三边,并且等于它
的一半
82 梯形中位线定理 梯形的中位线平行于两底,并且等于两底和的 一半 L=(a+b)÷2 S=L×h
83 (1)比例的基本性质 如果a:b=c:d,那么ad=bc
如果ad=bc,那么a:b=c:d
84 (2)合比性质 如果a/b=c/d,那么(a±b)/b=(c±d)/d
85 (3)等比性质 如果a/b=c/d=…=m/n(b+d+…+n≠0),那么
(a+c+…+m)/(b+d+…+n)=a/b
86 平行线分线段成比例定理 三条平行线截两条直线,所得的对应
线段成比例
87 推论 平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例
88 定理 如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边
89 平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例
90 定理 平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似
91 相似三角形判定定理1 两角对应相等,两三角形相似(ASA)
92 直角三角形被斜边上的高分成的两个直角三角形和原三角形相似
93 判定定理2 两边对应成比例且夹角相等,两三角形相似(SAS)
94 判定定理3 三边对应成比例,两三角形相似(SSS)
95 定理 如果一个直角三角形的斜边和一条直角边与另一个直角三
角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似
96 性质定理1 相似三角形对应高的比,对应中线的比与对应角平
分线的比都等于相似比
97 性质定理2 相似三角形周长的比等于相似比
98 性质定理3 相似三角形面积的比等于相似比的平方
107到已知角的两边距离相等的点的轨迹,是这个角的平分线
108到两条平行线距离相等的点的轨迹,是和这两条平行线平行且距离相等的一条直线
139正n边形的每个内角都等于(n-2)×180°/n
140定理 正n边形的半径和边心距把正n边形分成2n个全等的直角三角形
141正n边形的面积Sn=pnrn/2 p表示正n边形的周长
142正三角形面积√3a/4 a表示边长
143如果在一个顶点周围有k个正n边形的角,由于这些角的和应为
360°,因此k×(n-2)180°/n=360°化为(n-2)(k-2)=4
145扇形面积公式:S扇形=n兀R^2/360=LR/2
实用工具:常用数学公式
公式分类 公式表达式
乘法与因式分 a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b(a2+ab+b2)
三角不等式 |a+b|≤|a|+|b| |a-b|≤|a|+|b| |a|≤b-b≤a≤b
|a-b|≥|a|-|b| -|a|≤a≤|a|
一元二次方程的解 -b+√(b2-4ac)/2a -b-√(b2-4ac)/2a
根与系数的关系 X1+X2=-b/a X1*X2=c/a 注:韦达定理
判别式
b2-4ac=0 注:方程有两个相等的实根
b2-4ac>0 注:方程有两个不等的实根
b2-4ac1年前查看全部
- 如何证明托勒密定理圆内接四边形对边的乘积和等于对角线的乘积
 frjjtt摄影师1年前1
frjjtt摄影师1年前1 -
 chitangfish 共回答了17个问题
chitangfish 共回答了17个问题 |采纳率100%http://baike.baidu.com/view/148250.htm?fr=ala0_1_1
百度百科有的1年前查看全部
- 哪个位高手帮我证明下托勒密定理(数学)
 sake441年前1
sake441年前1 -
 极不要 共回答了11个问题
极不要 共回答了11个问题 |采纳率100%托勒密(Ptolemy)定理指出,圆内接凸四边形两对对边乘积的和等于两条对角线的乘积.
在直线上,托勒密定理同样成立,这时也称为欧拉定理.
托勒密定理的逆定理同样成立:一个凸四边形两对对边乘积的和等于两条对角线的乘积,则这个凸四边形内接于一圆.
推广及证明
* 托勒密不等式:四边形的任两组对边乘积不小于另外一组对边的乘积,取等号当且仅当共圆或共线.
o 简单的证明:复数恒等式:(a-b)(c-d)+(a-d)(b-c)=(a-c)(b-d),两边取模,得不等式,分析等号成立的条件.
o 四点不限于同一平面.1年前查看全部
- 关于平面几何定理的困惑要参加高中数学联赛的人都知道平面几何定理很多可我看不出有什么实用价值,有的书上竟然说托勒密定理很轻
关于平面几何定理的困惑
要参加高中数学联赛的人都知道平面几何定理很多
可我看不出有什么实用价值,有的书上竟然说托勒密定理很轻盈?
我觉得实在是笨重的可以,也可能是应用程度不够吧.
想听听大家的意见 werabma1年前1
werabma1年前1 -
 masya 共回答了7个问题
masya 共回答了7个问题 |采纳率85.7%我也要参加高中数学联赛,江苏的
我认为定理是很多,但要知道的不要太多
夏令营的时候,教我们平几的老师选的:1.托勒密定理 2.梅式定理 3.塞瓦定理 4.欧拉定理 5.西姆松线 6:斯特瓦特定理 我感觉这些是最基础的,而且现在联赛平几难度整体不算太大,去年不就是一个托勒密吗?掌握这些是必须的,其他你像什么牛顿定理之类的用来证线共点或点共线的定理可以看几个,不过我觉得有些定理记住了临场也想不太到,要是准备二试平几一定拿下的话就得多做题
托勒密是很轻盈,约束条件少嘛1年前查看全部
- 托勒密定理麻烦说下定义和一些简单的例题
 楚欲1年前2
楚欲1年前2 -
 fishny 共回答了19个问题
fishny 共回答了19个问题 |采纳率100%定理:若ABCD四点共圆(ABCD按顺序都在同一个圆上),那么AB.CD+BC.AD=AC.BD.
例题:(我讲道好玩的吧:)
证明对于任意正整数n都存在n个点使得所有点间两两距离为整数.
归纳法.我们用归纳法证明一个更强的定理:对于任意n都存在n个点使得所有点间两两距离为整数,且这n个点共圆,并且有两点是一条直径的两端.
n=1,n=2很轻松.
当n=3时,一个边长为整数的勾股三角形即可:比如说边长为3,4,5的三角形.我们发现这样的三个点共圆,边长最长的边是一条直径.
假设对于n大于等于3成立,我们来证明n+1.
假设直径为r(整数).找一个不跟已存在的以这个直径为斜边的三角形相似的一个整数勾股三角形ABC(边长a1年前查看全部
- 探究问题:(2)知识迁移:①请你利用托勒密定理,解决如下问题:如图(C),已知点P为等边△ABC外接圆的BC上任意一点.
探究问题:
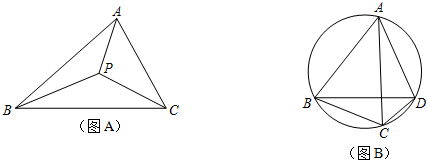
(2)知识迁移:
①请你利用托勒密定理,解决如下问题:
如图(c),已知点p为等边△abc外接圆的
上任意一点.求证:pb+pc=pa;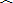
bc
②根据(2)①的结论,我们有如下探寻△abc(其中∠a、∠b、∠c均小于120°)的费马点和费马距离的方法:
第一步:如图(d),在△abc的外部以bc为边长作等边△bcd及其外接圆;
第二步:在
上任取一点p′,连接p′a、p′b、p′c、p′d.易知p′a+p′b+p′c=p′a+(p′b+p′c)=p′a+______;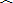
bc
第三步:请你根据(1)①中定义,在图(d)中找出△abc的费马点p,并请指出线段______的长度即为△abc的费马距离.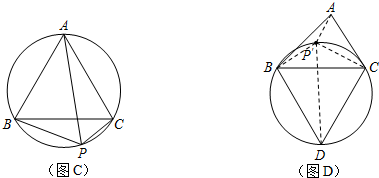
(3)知识应用:
2010年4月,我国西南地区出现了罕见的持续干旱现象,许多村庄出现了人、畜饮水困难,为解决老***饮水问题,***某部来到云南某地打井取水.
已知三村庄a、b、c构成了如图(e)所示的△abc(其中∠a、∠b、∠c均小于120°),现选取一点p打水井,使从水井p到三村庄a、b、c所铺设的输水管总长度最小,求输水管总长度的最小值.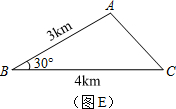
(1)阅读理解:
①如图(a),在已知△abc所在平面上存在一点p,使它到三角形顶点的距离之和最小,则称点p为△abc的费马点,此时pa+pb+pc的值为△abc的费马距离;
②如图(b),若四边形abcd的四个顶点在同一圆上,则有ab•cd+bc•da=ac•bd.此为托勒密定理;
 临时男主角1年前1
临时男主角1年前1 -
 jxk8167 共回答了19个问题
jxk8167 共回答了19个问题 |采纳率73.7%解题思路:(2)知识迁移①问,只需按照题意套用托勒密定理,再利用等边三角形三边相等,将所得等式两边都除以等边三角形的边长,即可获证. ②问,借用①问结论,及线段的性质“两点之间线段最短”数学容易获解.
(3)知识应用,在(2)的基础上先画出图形,再求解. (2)①证明:由托勒密定理可知PB•AC+PC•AB=PA•BC
(2)①证明:由托勒密定理可知PB•AC+PC•AB=PA•BC
∵△ABC是等边三角形
∴AB=AC=BC,
∴PB+PC=PA,
②P′D、AD,
(3)如图,以BC为边长在△ABC的外部作等边△BCD,连接AD,则知线段AD的长即为△ABC 的费马距离.
的费马距离.
∵△BCD为等边三角形,BC=4,
∴∠CBD=60°,BD=BC=4,
∵∠ABC=30°,∴∠ABD=90°,
在Rt△ABD中,∵AB=3,BD=4,
∴AD=
AB2+BD2=
32+42=5(km),
∴从水井P到三村庄A、B、C所铺设的输水管总长度的最小值为5km.点评:
本题考点: 等边三角形的性质;勾股定理;旋转的性质;相似三角形的判定与性质;解直角三角形.
考点点评: 此题是一个综合性很强的题目,主要考查等边三角形的性质、三角形相似、解直角三角形等知识.难度很大,有利于培养同学们钻研问题和探索问题的精神.1年前查看全部
- 凹四边形能用于托勒密定理的证明吗?
 lyylyy11年前1
lyylyy11年前1 -
 88037507 共回答了17个问题
88037507 共回答了17个问题 |采纳率88.2%凹四边形的四个点可以在一个圆上吗?1年前查看全部
- 托勒密定理的内容
 liangzhongwei1年前1
liangzhongwei1年前1 -
 寒潭孤羽 共回答了12个问题
寒潭孤羽 共回答了12个问题 |采纳率83.3%托勒密定理:
圆内接四边形ABCD的两组对边乘积的和等于它的两条对角线的乘积,即AB*CD+AD*BC=AC*BD.
过C作CP交BD于P,使∠1=∠2,又∠3=∠4,∴△ACD∽△BCP.
又∠ACB=∠DCP,∠5=∠6,∴△ACB∽△DCP.
①+②得 AC(BP+DP)=AB·CD+AD·BC.
即AC·BD=AB·CD+AD·BC.1年前查看全部
- 凹四边形能用于托勒密定理的证明吗?
凹四边形能用于托勒密定理的证明吗?
托勒密定理的证明中用的都是凸四边形,而且定理论述的也是圆内凸四边形的性质,那么请问为什么不能用凹四边形呢?能不能证明一下为什么不可以用凹四边形? lvy2281年前2
lvy2281年前2 -
 今夜单身 共回答了27个问题
今夜单身 共回答了27个问题 |采纳率85.2%凹四边形的四个点可以在一个圆上吗?1年前查看全部
- 梅涅劳斯定理、塞瓦定理、托勒密定理、西姆松定理是什么?
 lindsay_liu1年前1
lindsay_liu1年前1 -
 胖胖的蝾螈 共回答了19个问题
胖胖的蝾螈 共回答了19个问题 |采纳率84.2%找到了
很久以前学的了
忘的差不多了1年前查看全部
- 谁会用相似证托勒密定理,是圆内接四边形,不要百度百科上的!
 试用版1年前1
试用版1年前1 -
 空留月光 共回答了23个问题
空留月光 共回答了23个问题 |采纳率78.3%设圆内接四边形ABCD
作角BAE=角CAD(E在BD上)
证明△ABE与△ACD相似,再证明三角形ABC与三江乡AED相似就可以了
百科上是这个方法吗?1年前查看全部
- 求初中课外的几何定理,如托勒密定理、梅氏定理…………
求初中课外的几何定理,如托勒密定理、梅氏定理…………
RT,要所有的 乐东鬼1年前2
乐东鬼1年前2 -
 tltlttll 共回答了16个问题
tltlttll 共回答了16个问题 |采纳率93.8%我可以给你一些,记不全了(要看定理具体内容自己搜索):
赛瓦定理、西姆松定理、圆幂定理、婆罗摩笈多定理、卡诺定理、欧拉定理、中线长定理、斯特瓦尔特定理、角平分线定理(广义)、正(余)弦定理.能称得上定理的我就记得这些了.还有那个九点圆,记不清怎么回事了;海伦公式,很实用(四边形也有相似的不等式)
PS:1.我现在初三,没听着老师说这些定理是不是初中的.还有老师说高中就没有平面几何了.所以估计几何定理初中联赛都用得上.1年前查看全部
- 梅涅劳斯定理,塞瓦定理,托勒密定理,西姆松定理四大定理的描述
 道格拉斯bear1年前1
道格拉斯bear1年前1 -
 青青子衿06 共回答了18个问题
青青子衿06 共回答了18个问题 |采纳率77.8%梅涅劳斯定理
如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么(AF/FB)×(BD/DC)×(CE/EA)=1.
赛瓦定理
设O是△ABC内任意一点,AO、BO、CO分别交对边于D、E、F,则 BD/DC*CE/EA*AF/FB=1.
托勒密定理
圆内接凸四边形两对对边乘积的和等于两条对角线的乘积.
西姆松定理
从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上.1年前查看全部
大家在问
- 1《浮生六记》中“神游其中,怡然自得”这句话什么意思?拜托各位了 3Q
- 2面积30平方,比例为16:9,怎么换算出长与宽?
- 3钱塘湖春行的诗意是什么,最好是短一点的
- 4急求八年级下册数学华师大版的所有黑体字!
- 5氨水和氯化钙怎么生成碳酸钙?
- 6拎.可以组成什么组词
- 7描写莲花的文章结尾我以莲花,不朽的传奇为题目,怎么写结尾?
- 8求剑桥雅思6 TEST4阅读部分的答案
- 9求作文 不灭的灯火以不灭的灯火为题800字作文...
- 10求导时可不可以带入等价无穷小来求?
- 11求问为什么红光比蓝紫光光合作用效率更高?
- 12比如矩阵和向量都不满足消去律,那请问具体满足什么条件下,一定能够满足消去律?比如我随便写个方程:yx^2+yx=x+y^
- 13五年级上册语文第14课怎么分段
- 14下列词语中错别字最多 下列词语中错别字最多的一项是 [ ] A.狡狯 黄连 主弦律 歇嘶底里
- 15end.up 造句 不要直接 end up 要难点的 平常的 家翻译