P是双曲线x23−y2=1的右支上一动点,F是双曲线的右焦点,已知A(3,1),则|PA|+|PF|的最小值为_____
 gao95102022-10-04 11:39:541条回答
gao95102022-10-04 11:39:541条回答| x2 |
| 3 |

已提交,审核后显示!提交回复
共1条回复
 紫榭 共回答了10个问题
紫榭 共回答了10个问题 |采纳率100%- 解题思路:设双曲线左焦点为F2,根据双曲线的定义可知|PA|+|PF|=|PF2|-2a+|PA|,进而可知当P、F2、A三点共线时有最小值,根据双曲线方程可求的F2的坐标,此时|PF2|+|PA|=|AF2|,利用两点间的距离公式求得答案.
设双曲线左焦点为F2,则|PA|+|PF|=|PF2|-2a+|PA|=
当P、F2、A三点共线时有最小值,此时F2(-2,0)、A(3,1)所以
|PF2|+|PA|=|AF2|=
26,而对于这个双曲线,2a=2
3,
所以最小值为
26-2
3
故答案为
26-2
3点评:
本题考点: 双曲线的应用;双曲线的简单性质.
考点点评: 本题主要考查了双曲线的应用.解题的过程灵活运用了双曲线的定义和用数形结合的方法解决问题. - 1年前
相关推荐
- 已知椭圆C:x2a2+y2b2=1(a>b>0)与双曲线x23-y2=1共焦点,点A(3,7)在椭圆C上.
已知椭圆C:
+x2 a2
=1(a>b>0)与双曲线y2 b2
-y2=1共焦点,点A(3,x2 3
)在椭圆C上.7
(1)求椭圆C的方程;
(2)已知点Q(0,2),P为椭圆C上的动点,点M满足:
=QM
,求动点M的轨迹方程.MP
 丫头张1年前1
丫头张1年前1 -
 森林木林 共回答了22个问题
森林木林 共回答了22个问题 |采纳率86.4%解题思路:(1)根据椭圆与双曲线公焦点,可知椭圆的焦点坐标,利用点A(3,
)在椭圆C上,根据椭圆的定义,我们可以求出a的值,根据焦点坐标,利用b2=a2-c2,可以求出b2,从而可求椭圆C的方程;7
(2)利用点M满足:
=QM
,可得动点M与动点P之间的坐标关系,利用点P满足椭圆方程,我们可以求出动点M的轨迹方程.MP (1)由已知得双曲线焦点坐标为F1(-2,0),F2(2,0),
由椭圆的定义得|AF1|+|AF2|=2a,∴
25+7+
1+7=2a,∴a=3
2
而c2=4,∴b2=a2-c2=18-4=14
∴所求椭圆方程为
x2
18+
y2
14=1
(2)设M(x,y),P(x0,y0),由
QM=
MP得(x,y-2)=(x0-x,y0-y)
∴
x0=2x
y0=2y-2而P(x0,y0)在椭圆
x2
18+
y2
14=1上
即
(2x)2
18+
(2y-2)2
14=1
即
2x2
9+
2(y-1)2
7=1为所求M的轨迹方程.点评:
本题考点: 椭圆的标准方程;轨迹方程.
考点点评: 本题的考点是椭圆的标准方程,考查待定系数法求椭圆的标准方程,考查代入法求轨迹方程,解题的关键是利用向量关系,寻求动点之间的坐标关系.1年前查看全部
- (2014•韶关模拟)如图,已知抛物线y2=2px的焦点F与双曲线x23-y2=1的右焦点重合,过抛物线焦点F的直线交该
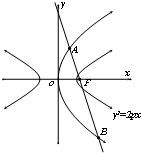 (2014•韶关模拟)如图,已知抛物线y2=2px的焦点F与双曲线
(2014•韶关模拟)如图,已知抛物线y2=2px的焦点F与双曲线
-y2=1的右焦点重合,过抛物线焦点F的直线交该抛物线于A,B两点,|AF|=3,则p=______;直线AB斜率等于x2 3 -22 -2.2  heaton55821年前1
heaton55821年前1 -
 8671680 共回答了24个问题
8671680 共回答了24个问题 |采纳率87.5%解题思路:求出双曲线
-y2=1的右焦点,可得p与抛物线方程,利用抛物线的定义,可得A的坐标,即可求出直线AB斜率.x2 3 双曲线
x2
3-y2=1的右焦点为(2,0),∴抛物线方程为y2=8x,p=4.
∵|AF|=3,∴xA+2=3,∴xA=1
代入抛物线方程可得yA=±2
2
∵点A在x轴上方,∴A(1,2
2),
∴直线AB斜率等于
2
2
1−2=-2
2.
故答案为:4,-2
2.点评:
本题考点: 抛物线的简单性质;双曲线的简单性质.
考点点评: 本题考查抛物线、双曲线的性质,考查学生的计算能力,比较基础.1年前查看全部
- 设椭圆x26+y22=1与双曲线x23-y2=1有公共焦点为F1,F2,P是两条曲线的一个公共点,则cos∠F1PF2的
设椭圆
+x2 6
=1与双曲线y2 2
-y2=1有公共焦点为F1,F2,P是两条曲线的一个公共点,则cos∠F1PF2的值等于( )x2 3
A.[1/4]
B.[1/3]
C.[1/9]
D.[3/5] 夏朝春1年前1
夏朝春1年前1 -
 小玦 共回答了25个问题
小玦 共回答了25个问题 |采纳率96%解题思路:先求出公共焦点分别为F1,F2,再联立方程组求出P,由此可以求出 PF1和PF2,cos∠F1PF2=PF1•PF2|PF1|•|PF2|由题意知F1(-2,0),F2(2,0),
解方程组
x2
6+
y2
2=1
x2
3−y2=1得
x2=
9
2
y2=
1
2取P点坐标为(
3
2
2,
2
2),
PF1=(−2−
3
2
2,−
2
2),
PF2=(2−
3
2
2,−
2
2)
cos∠F1PF2=
(−2−
3
2
2)• (2−
3
2
2)+
1
2
(−2−
3
2
2)2+
1
2•
(2−
3
2
2)2+
1
2=[1/3]
故选B.点评:
本题考点: 圆锥曲线的共同特征.
考点点评: 本题考查圆锥曲线的性质和应用,解题时要注意公式的灵活运用.1年前查看全部
- 若抛物线y2=-2px(p>0)的焦点与双曲线x23−y2=1的左焦点重合,则p的值______.
 52344261年前1
52344261年前1 -
 q8711917 共回答了16个问题
q8711917 共回答了16个问题 |采纳率81.3%解题思路:先求双曲线的左焦点,再利用抛物线y2=-2px(p>0)的焦点与双曲线
−y2=1的左焦点重合,可求p的值.x2 3 双曲线
x2
3−y2=1的左焦点为(-2,0)
∵抛物线y2=-2px(p>0)的焦点与双曲线
x2
3−y2=1的左焦点重合,
∴
p
2=2
∴p=4
故答案为:4点评:
本题考点: 圆锥曲线的共同特征.
考点点评: 本题考查双曲线的几何性质,考查抛物线的标准方程,属于中档题.1年前查看全部
- (2014•兴安盟一模)已如点M(1,0)及双曲线x23−y2=1的右支上两动点A,B,当∠AMB最大时,它的余弦值为(
(2014•兴安盟一模)已如点M(1,0)及双曲线
−y2=1的右支上两动点A,B,当∠AMB最大时,它的余弦值为( )x2 3
A. -[1/2]
B. [1/2]
C. -[1/3]
D. [1/3] wwn88881年前0
wwn88881年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 已知抛物线的顶点在原点,抛物线的焦点和双曲线x23−y2=1的右焦点重合,则抛物线的方程为______.
 wangwanzhao01021年前1
wangwanzhao01021年前1 -
 amartya1888 共回答了8个问题
amartya1888 共回答了8个问题 |采纳率100%解题思路:由双曲线得右焦点坐标,从而可得抛物线的焦点坐标,进而写出抛物线方程.由题意,双曲线
x2
3−y2=1的右焦点为(2,0)
∴抛物线的焦点坐标为(2,0)
设抛物线的方程为:y2=2px(p>0)
∴[p/2]=2,∴p=4,
∴抛物线方程是 y2=8x.
故答案为:y2=8x.点评:
本题考点: 双曲线的简单性质;抛物线的标准方程.
考点点评: 本题考查双曲线的简单性质及抛物线的标准方程,解题的关键是由双曲线的焦点坐标得出抛物线的焦点坐标.属于基础题.1年前查看全部
- (2011•晋中三模)已知抛物线的顶点在原点,抛物线的焦点和双曲线x23−y2=1的右焦点重合,则抛物线的方程为____
(2011•晋中三模)已知抛物线的顶点在原点,抛物线的焦点和双曲线
−y2=1的右焦点重合,则抛物线的方程为______.x2 3  无敌床上飞1年前1
无敌床上飞1年前1 -
 贴过海报 共回答了26个问题
贴过海报 共回答了26个问题 |采纳率84.6%解题思路:由双曲线得右焦点坐标,从而可得抛物线的焦点坐标,进而写出抛物线方程.由题意,双曲线
x2
3−y2=1的右焦点为(2,0)
∴抛物线的焦点坐标为(2,0)
设抛物线的方程为:y2=2px(p>0)
∴[p/2]=2,∴p=4,
∴抛物线方程是 y2=8x.
故答案为:y2=8x.点评:
本题考点: 双曲线的简单性质;抛物线的标准方程.
考点点评: 本题考查双曲线的简单性质及抛物线的标准方程,解题的关键是由双曲线的焦点坐标得出抛物线的焦点坐标.属于基础题.1年前查看全部
- 若抛物线y2=2px的焦点与双曲线x23-y2=1的左焦点重合,则实数p=______.
 AppleTTTcn1年前1
AppleTTTcn1年前1 -
 yqyq11 共回答了17个问题
yqyq11 共回答了17个问题 |采纳率88.2%抛物线的焦点F为([p/2],0),
双曲线
x2
3-y2=1的左焦点F2(-2,0),
由已知得[p/2]=-2,
∴p=-4.
故答案为:-4.1年前查看全部
- (2014•漳州三模)设F1,F2是双曲线x23−y2=1的两个焦点,P在双曲线上,当△F1PF2的面积为2时,PF1•
(2014•漳州三模)设F1,F2是双曲线
−y2=1的两个焦点,P在双曲线上,当△F1PF2的面积为2时,x2 3
•PF1
的值为( )PF2
A. 2
B. 3
C. 4
D. 6 thysigh_yssn1年前1
thysigh_yssn1年前1 -
 zbgoodboy 共回答了21个问题
zbgoodboy 共回答了21个问题 |采纳率85.7%解题思路:求得双曲线的焦点坐标,利用△F1PF2的面积为2,确定P的坐标,利用向量的数量积公式,即可求得结论.双曲线
x2
3−y2=1的两个焦点坐标为F1(-2,0),F2(2,0)
设P的坐标为(x,y),则
∵△F1PF2的面积为2
∴[1/2×4×|y|=2
∴|y|=1,代入双曲线方程解得|x|=
6]
∴
PF1•
PF2=(-2-x,-y)•(2-x,-y)=x2-4+y2=3
故选B.点评:
本题考点: 双曲线的应用.
考点点评: 本题考查双曲线的几何性质,考查向量的数量积运算,确定P的坐标是关键.1年前查看全部
- (2010•蓟县一模)若抛物线y2=2ax(a≠0)的焦点与双曲线x23-y2=1的左焦点重合,则a的值为( )
(2010•蓟县一模)若抛物线y2=2ax(a≠0)的焦点与双曲线
-y2=1的左焦点重合,则a的值为( )x2 3
A.-2
B.-4
C.2
D.4 fth16881年前1
fth16881年前1 -
 cb0911 共回答了14个问题
cb0911 共回答了14个问题 |采纳率100%解题思路:根据双曲线的方程,可得a2=3,b2=1,由此算出c=2.因此得到双曲线的左焦点坐标为F(-2,0)也是抛物线的焦点,结合抛物线的焦点坐标公式建立关于a的等式,解之即可得到实数a的值.∵双曲线的方程为
x2
3-y2=1,
∴a2=3,b2=1可得c=2
因此,双曲线的左焦点坐标为F(-2,0)
∵抛物线y2=2ax的焦点与双曲线
x2
3-y2=1的左焦点重合,
∴-[a/2]=2,解之得a=4
故选:B.点评:
本题考点: 双曲线的简单性质;抛物线的简单性质.
考点点评: 本题给出抛物线与已知双曲线有公共的焦点,求抛物线的方程.着重考查了抛物线、双曲线的标准方程与简单几何性质等知识,属于基础题.1年前查看全部
- (2011•江苏二模)若抛物线y2=2px的焦点与双曲线x23-y2=1的右焦点重合,则实数p=______.
 yy车1年前1
yy车1年前1 -
 00011rr 共回答了17个问题
00011rr 共回答了17个问题 |采纳率100%解题思路:先分别求出抛物线和双曲线的焦点,让二者相等即可得到答案.抛物线的焦点F为([p/2],0),
双曲线
x2
3-y2=1的右焦点F2(2,0),
由已知得[p/2]=2,
∴p=4.
故答案为4点评:
本题考点: 圆锥曲线的共同特征.
考点点评: 本题主要考查了圆锥曲线的共同特征.属基础题.1年前查看全部
- 已知椭圆与双曲线x23−y2=1有共同的焦点,且过点P(2,3),求双曲线的渐近线及椭圆的方程.
 dahai_961年前1
dahai_961年前1 -
 jinshan2000 共回答了11个问题
jinshan2000 共回答了11个问题 |采纳率90.9%解题思路:先把曲线的标准标准方程,其渐近线方程是
−y2=0,整理后就得到双曲线的渐近线方程.利用椭圆与双曲线有共同的焦点F1(-2,0),F2(2,0),设出椭圆方程,再利用点P(2,3)适合椭圆方程,就可求出椭圆的方程.x2 3 双曲线的标准形式为
x2
3−y2=1,
其渐近线方程是
x2
3−y2=0,
整理得双曲线的渐近线为:x±
3y=0.
由共同的焦点F1(-2,0),F2(2,0),可设椭圆方程为
y2
a2+
x2
b2=1,
点P(2,3)在椭圆上,
4
a2+
9
b2=1
a 2−b 2=4,
∴a2=16,b2=12,
所以椭圆方程为:
y2
16+
x2
12=1.点评:
本题考点: 圆锥曲线的共同特征.
考点点评: 本题考查本题考查双曲线的标准方程,以及椭圆的标准方程的求法,令标准方程中的“1”为“0”即可求出渐近线方程.在求双曲线与椭圆的标准方程时,一定要先分析焦点所在位置,再设方程,避免出错.1年前查看全部
- (2013•朝阳区一模)以双曲线x23−y2=1的右焦点为焦点,顶点在原点的抛物线的标准方程是______.
 kanesman1年前1
kanesman1年前1 -
 tajssz 共回答了12个问题
tajssz 共回答了12个问题 |采纳率100%解题思路:根据双曲线方程,算出它的右焦点为F(2,0),也是抛物线的焦点.由此设出抛物线方程为y2=2px,(p>0),结合抛物线焦点坐标的公式,可得p=4,从而得出该抛物线的标准方程.∵双曲线的方程为
x2
3−y2=1,
∴a2=3,b2=1,得c=2,
∴双曲线的右焦点为F(2,0),也是抛物线的焦点
设抛物线方程为y2=2px,(p>0),则[p/2]=2,得2p=8
∴抛物线方程是y2=8x.
故答案为:y2=8x.点评:
本题考点: 抛物线的标准方程;双曲线的简单性质.
考点点评: 本题给出抛物线焦点与已知双曲线的右焦点重合,求抛物线的标准方程,着重考查了双曲线、抛物线的标准方程与简单几何性质等知识,属于基础题.1年前查看全部
- 下列曲线中,与双曲线x23-y2=1的离心率和渐近线都相同的是( )
下列曲线中,与双曲线
-y2=1的离心率和渐近线都相同的是( )x2 3
A.
-x2 3
=1y2 9
B.
−y2 3
=1x2 9
C.
−x2 9
=1y2 3
D.
-x2=1y2 3  渤海飒1年前0
渤海飒1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 已知双曲线C与双曲线x23−y2=1有相同的渐近线,且过点A(3,-3),则双曲线C的标准方程是y28−x224=1y2
已知双曲线C与双曲线
−y2=1有相同的渐近线,且过点A(x2 3
,-3),则双曲线C的标准方程是3
−y2 8
=1x2 24 .
−y2 8
=1x2 24  erwuying1年前1
erwuying1年前1 -
 wzjackson 共回答了17个问题
wzjackson 共回答了17个问题 |采纳率88.2%解题思路:由于双曲线C与双曲线有
−y2=1相同的渐近线,则可设C的方程是x2 3
−y2=λ(λ≠0),再由点A在双曲线上,即可得到λ的值,进而得到双曲线C的标准方程.x2 3 由于双曲线C与双曲线有
x2
3−y2=1相同的渐近线,
则可设C的方程是
x2
3−y2=λ(λ≠0),
又过点A(
3,-3),则λ=-8,
即C的方程是
y2
8−
x2
24=1.
故答案为:
y2
8−
x2
24=1.点评:
本题考点: 双曲线的简单性质.
考点点评: 本题着重考查了双曲线的标准方程与简单几何性质等知识,属于基础题.1年前查看全部
- 已知双曲线x23-y2n−12=1的离心率是3,则n=______.
 wwwttt5791年前1
wwwttt5791年前1 -
 可爱小薇 共回答了18个问题
可爱小薇 共回答了18个问题 |采纳率100%解题思路:利用离心率定义及c2=a2+b2,求出n即可.∵双曲线
x2
3-
y2
n−12=1的离心率是
3,
∴e2=[3+n−12/3]=3
∴n=18,
故答案为:18.点评:
本题考点: 双曲线的简单性质.
考点点评: 本题考查了双曲线的标准方程及其几何性质,属基础题1年前查看全部
- 抛物线y2=2px的焦点与双曲线x23−y2=1的右焦点重合.
抛物线y2=2px的焦点与双曲线
−y2=1的右焦点重合.x2 3
(Ⅰ)求抛物线的方程;
(Ⅱ)求抛物线的准线与双曲线的渐近线围成的三角形的面积. 秋冷雨寒1年前1
秋冷雨寒1年前1 -
 dongaj 共回答了19个问题
dongaj 共回答了19个问题 |采纳率84.2%解题思路:(Ⅰ)由双曲线方程求出其半焦距,根据抛物线的焦点与双曲线右焦点重合求出P,从而求出抛物线方程;
(Ⅱ)分别求出抛物线的准线方程和双曲线的渐近线方程,联立求出两交点间的距离,然后直接代入三角形的面积公式求解.(Ⅰ)由双曲线
x2
3−y2=1得,a2=3,b2=1,
所以c2=a2+b2=3+1=4,所以c=2.
则[p/2=2,p=4.
所以抛物线的方程为y2=8x;
(Ⅱ)由题意知,a=
3,b=1,
所以双曲线的渐近线方程为y=±
3
3x,
抛物线的准线方程为x=-2.
代入双曲线的准线方程得y=±
2
3
3].
设抛物线的准线与双曲线的准线的交点为A,B.
则|AB|=
4
3
3.
所以抛物线的准线与双曲线的渐近线围成的三角形的面积为:
S=
1
2×
4
3
3×2=
4
3
3.点评:
本题考点: 圆锥曲线的轨迹问题.
考点点评: 本题考查了圆锥曲线的轨迹问题,两圆锥曲线的关系问题是高考常见题型,解答的关键是合理运用所涉及的量,
此类问题往往具有较复杂的运算量,考查学生的计算能力,此题是中档题.1年前查看全部
- 若抛物线y2=2px的焦点与双曲线x23−y2=1的右焦点重合,则p的值为( )
若抛物线y2=2px的焦点与双曲线
−y2=1的右焦点重合,则p的值为( )x2 3
A. -4
B. 4
C. -2
D. 2 ktotrdd871年前2
ktotrdd871年前2 -
 荣求王志 共回答了28个问题
荣求王志 共回答了28个问题 |采纳率85.7%解题思路:根据双曲线方程可得它的右焦点坐标,结合抛物线y2=2px的焦点坐标([p/2],0),可得[p/2]=2,得p=4.∵双曲线
x2
3−y2=1中a2=3,b2=1
∴c=
a2+b2=2,得双曲线的右焦点为F(2,0)
因此抛物线y2=2px的焦点([p/2],0)即F(2,0)
∴[p/2]=2,即p=4
故选B点评:
本题考点: 抛物线的简单性质.
考点点评: 本题给出双曲线的焦点与抛物线焦点重合,求抛物线的焦参数,着重考查了双曲线的基本概念和抛物线的标准方程等知识,属于基础题.1年前查看全部
- 已知椭圆x2a2+y2b2=1(a>b>0)的一个顶点为A(0,1),且它的离心率与双曲线x23-y2=1的离心率互为倒
已知椭圆
+x2 a2
=1(a>b>0)的一个顶点为A(0,1),且它的离心率与双曲线y2 b2
-y2=1的离心率互为倒数.x2 3
(1)求椭圆的方程;
(2)过点A且斜率为k的直线l与椭圆相交于A、B两点,点M在椭圆上,且满足
=[1/2]OM
+OA 3 2
,求k的值.OB  kt308bwsgracdnj1年前1
kt308bwsgracdnj1年前1 -
 我调查我oo 共回答了19个问题
我调查我oo 共回答了19个问题 |采纳率89.5%解题思路:(1)根据双曲线的标准方程,可得其离心率,进而根据题设可求得椭圆的离心率.再根据椭圆的顶点A的坐标,进而可求得b和a,椭圆的方程可得.
(2)先设直线l的方程为y=kx+1,A(x1,y1),B(x2,y2),M(m,n),直线和椭圆相交,联立方程可得含有k的一元二次方程,再根据韦达定理可知x1+x2和x1•x2,再根据
=[1/2]OM
+OA 3 2
,用点A,B表示点M,代入椭圆的标准方程可得k.OB (1)∵双曲线-y2=1的离心率为
2
3
3,
∴椭圆的离心率为
3
2.
又∵b=1,∴a=2.
∴椭圆的方程为
x2
4+y2=1.
(2)设直线l的方程为y=kx+1,A(x1,y1),B(x2,y2),M(m,n).
由
y=kx+1
x2
4+y2=1得(1+4k2)x2+8kx=0,
∴x1+x2=-[8k
1+4k2,x1•x2=0.
∵
/OM]=[1/2]
OA+点评:
本题考点: 椭圆的标准方程;直线与圆锥曲线的综合问题.
考点点评: 本题主要考查了椭圆的标准方程问题.当研究椭圆和直线的关系的问题时,常可利用联立方程,进而利用韦达定理来解决.1年前查看全部
- 已知抛物线C:y2=2px与双曲线x23-y2=1的右焦点重合,则抛物线C上的动点M到直线l1:4x-3y+6=0和l2
已知抛物线C:y2=2px与双曲线x23-y2=1的右焦点重合,则抛物线C上的动点M到直线l1:4x-3y+6=0和l2:x=-2距
已知抛物线C:y2=2px与双曲线
-y2=1的右焦点重合,则抛物线C上的动点M到直线l1:4x-3y+6=0和l2:x=-2距离之和的最小值为x2 3 [14/5][14/5].
 白羽离潇1年前0
白羽离潇1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 已知椭圆C:x2a2+y2b2=1(a>b>0)与双曲线x23−y2=1共焦点,点A(3,7)在椭圆C上.
已知椭圆C:
+x2 a2
=1(a>b>0)与双曲线y2 b2
−y2=1共焦点,点A(3,x2 3
)在椭圆C上.7
(1)求椭圆C的方程;
(2)已知点Q(0,2),P为椭圆C上的动点,点M满足:
=QM
,求动点M的轨迹方程.MP  令狐摄影1年前1
令狐摄影1年前1 -
 空无千 共回答了19个问题
空无千 共回答了19个问题 |采纳率89.5%解题思路:(1)根据椭圆与双曲线公焦点,可知椭圆的焦点坐标,利用点A(3,
)在椭圆C上,根据椭圆的定义,我们可以求出a的值,根据焦点坐标,利用b2=a2-c2,可以求出b2,从而可求椭圆C的方程;7
(2)利用点M满足:
=QM
,可得动点M与动点P之间的坐标关系,利用点P满足椭圆方程,我们可以求出动点M的轨迹方程.MP (1)由已知得双曲线焦点坐标为F1(-2,0),F2(2,0),
由椭圆的定义得|AF1|+|AF2|=2a,∴
25+7+
1+7=2a,∴a=3
2
而c2=4,∴b2=a2-c2=18-4=14
∴所求椭圆方程为
x2
18+
y2
14=1
(2)设M(x,y),P(x0,y0),由
QM=
MP得(x,y-2)=(x0-x,y0-y)
∴
x0=2x
y0=2y−2而P(x0,y0)在椭圆
x2
18+
y2
14=1上
即点评:
本题考点: 椭圆的标准方程;轨迹方程.
考点点评: 本题的考点是椭圆的标准方程,考查待定系数法求椭圆的标准方程,考查代入法求轨迹方程,解题的关键是利用向量关系,寻求动点之间的坐标关系.1年前查看全部
- (2014•马鞍山三模)椭圆x26+y22=1和双曲线x23-y2=1的公共焦点为F1、F2,P是两曲线的一个交点,那么
(2014•马鞍山三模)椭圆
+x2 6
=1和双曲线y2 2
-y2=1的公共焦点为F1、F2,P是两曲线的一个交点,那么cos∠F1PF2的值是x2 3 [1/3][1/3]. 与天共渺老二1年前1
与天共渺老二1年前1 -
 zb3551458 共回答了22个问题
zb3551458 共回答了22个问题 |采纳率95.5%解题思路:先求出公共焦点分别为F1,F2,再联立方程组求出P,由此可以求出
和PF1
,最后根据公式cos∠F1PF2=PF2
进行求解即可.
•PF1 PF2 |
|•|PF1
|PF2 由题意知F1(-2,0),F2(2,0),
解方程组
x2
6+
y2
2=1
x2
3−y2=1得
x2=
9
2
y2=
1
2,
取P点坐标为(
3
2
2,
2
2),点评:
本题考点: 圆锥曲线的共同特征.
考点点评: 本题考查圆锥曲线的性质和应用,解题时要注意公式的灵活运用,属基础题.1年前查看全部
- (2014•兴安盟一模)已如点M(1,0)及双曲线x23−y2=1的右支上两动点A,B,当∠AMB最大时,它的余弦值为(
(2014•兴安盟一模)已如点M(1,0)及双曲线
−y2=1的右支上两动点A,B,当∠AMB最大时,它的余弦值为( )x2 3
A.-[1/2]
B.[1/2]
C.-[1/3]
D.[1/3] rainway5211年前1
rainway5211年前1 -
 宋斌甲 共回答了22个问题
宋斌甲 共回答了22个问题 |采纳率95.5%解题思路:根据题意,当直线MA、MB分别与双曲线相切于点A、B时,可得∠AMB取得最大值.因此设直线AM方程为y=k(x-1),与双曲线联解并利用根的判别式,解出k=
.设直线AM倾斜角为θ,得∠AMB=2θ且tanθ=2 2
,最后利用二倍角的三角函数公式,即可算出∠AMB达到最大值时∠AMB的余弦值.2 2 根据题意,当直线
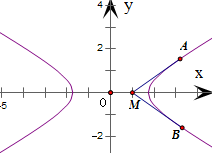 MA与双曲线相切于点A,直线MB与双曲线相切于点B时,
MA与双曲线相切于点A,直线MB与双曲线相切于点B时,
∠AMB取得最大值.
设直线AM方程为y=k(x-1),与双曲线消去y,得
([1/3]-k2)x2+2k2x-k2-1=0
∵直线MA与双曲线相切于点A,
∴(2k2)2-4×([1/3]-k2)×(-k2-1)=0,解之得k=
2
2(舍负)
因此,直线AM方程为y=
2
2(x-1),
同理直线BM方程为y=-
2
2(x-1),
设直线AM倾斜角为θ,得tanθ=
2
2,且∠AMB=2θ
∴cos2θ=
1−tan2θ
1+tan2θ=
1−
1
2
1+
1
2=[1/3],即为∠AMB最大时的余弦值
故选:D点评:
本题考点: 双曲线的简单性质;余弦定理.
考点点评: 本题给出双曲线方程和点M(1,0),求双曲线右支上两点A、B对M的最大张角的余弦之值,着重考查了双曲线的简单几何性质和直线与双曲线的位置关系等知识,属于中档题.1年前查看全部
- 以双曲线x23-y2=1的右焦点为焦点,顶点在原点的抛物线标准方程是( )
以双曲线
-y2=1的右焦点为焦点,顶点在原点的抛物线标准方程是( )x2 3
A.y2=4x
B.y2=-4x
C.y2=8x
D.y2=-8x 有明袁大将军1年前1
有明袁大将军1年前1 -
 心忧 共回答了22个问题
心忧 共回答了22个问题 |采纳率100%解题思路:先根据双曲线的方程求得其右焦点的坐标,进而设出抛物线的标准方程求得p,则抛物线的方程可得.∵双曲线
x2
3-y2=1,
∴c=
3+1=2,
∴双曲线的右焦点为:(2,0),
设抛物线的标准方程为y2=2px,
则[p/2]=2,p=4
∴抛物线标准方程为y2=8x,
故选C.点评:
本题考点: 抛物线的标准方程;双曲线的简单性质.
考点点评: 本题主要考查了抛物线的标准方程问题.较为基础,属基础题.1年前查看全部
- 若抛物线y2=2px的焦点与双曲线x23−y2=1的右焦点重合,则p的值为( )
若抛物线y2=2px的焦点与双曲线
−y2=1的右焦点重合,则p的值为( )x2 3
A. -4
B. 4
C. -2
D. 2 逗乐你想吗1年前1
逗乐你想吗1年前1 -
 多拉A梦的小口袋 共回答了17个问题
多拉A梦的小口袋 共回答了17个问题 |采纳率82.4%解题思路:根据双曲线方程可得它的右焦点坐标,结合抛物线y2=2px的焦点坐标([p/2],0),可得[p/2]=2,得p=4.∵双曲线
x2
3−y2=1中a2=3,b2=1
∴c=
a2+b2=2,得双曲线的右焦点为F(2,0)
因此抛物线y2=2px的焦点([p/2],0)即F(2,0)
∴[p/2]=2,即p=4
故选B点评:
本题考点: 抛物线的简单性质.
考点点评: 本题给出双曲线的焦点与抛物线焦点重合,求抛物线的焦参数,着重考查了双曲线的基本概念和抛物线的标准方程等知识,属于基础题.1年前查看全部
- 若抛物线y2=2px的焦点与双曲线x23−y2=1的右焦点重合,则p的值为( )
若抛物线y2=2px的焦点与双曲线
−y2=1的右焦点重合,则p的值为( )x2 3
A. -4
B. 4
C. -2
D. 2 starsky_11年前1
starsky_11年前1 -
 waffie 共回答了26个问题
waffie 共回答了26个问题 |采纳率88.5%解题思路:根据双曲线方程可得它的右焦点坐标,结合抛物线y2=2px的焦点坐标([p/2],0),可得[p/2]=2,得p=4.∵双曲线
x2
3−y2=1中a2=3,b2=1
∴c=
a2+b2=2,得双曲线的右焦点为F(2,0)
因此抛物线y2=2px的焦点([p/2],0)即F(2,0)
∴[p/2]=2,即p=4
故选B点评:
本题考点: 抛物线的简单性质.
考点点评: 本题给出双曲线的焦点与抛物线焦点重合,求抛物线的焦参数,着重考查了双曲线的基本概念和抛物线的标准方程等知识,属于基础题.1年前查看全部
- 椭圆的中心是原点O,它的短轴长为22,椭圆与双曲线x23-y2=1有共同的焦点.
椭圆的中心是原点O,它的短轴长为2
,椭圆与双曲线2
-y2=1有共同的焦点.x2 3
(1)求椭圆的方程;
(2)过点A(3,0)的直线与椭圆相交于不同的P、Q两点,求该直线斜率k的取值范围. cc1年前1
cc1年前1 -
 籽兮兮 共回答了19个问题
籽兮兮 共回答了19个问题 |采纳率73.7%解题思路:(1)由题意,可设椭圆的方程为
+x2 a2
=1(a>y2 2
).由双曲线2
-y2=1可得c=2.由已知得x2 3
,解出即可.a2−c2=2 c=2
(2)由题意可得A(3,0).设直线PQ的方程为y=k(x-3).与椭圆的方程联立化为(3k2+1)x2-18k2x+27k2-6=0.由△>0解出即可.(1)由题意,可设椭圆的方程为
x2
a2+
y2
2=1(a>
2).
由双曲线
x2
3-y2=1可得c2=3+1=4,解得c=2.
由已知得
a2−c2=2
c=2,解得a=
6,c=2.
∴椭圆的方程为
x2
6+
y2
2=1.
(2)由题意可得A(3,0).设直线PQ的方程为y=k(x-3).
联立
y=k(x−3)
x2+3y2=6,化为(3k2+1)x2-18k2x+27k2-6=0.
依题意△=324k2-4(3k2+1)(27k2-6)>0,得−
6
3<k<
6
3.点评:
本题考点: 直线与圆锥曲线的关系;椭圆的标准方程.
考点点评: 本题考查了椭圆与双曲线的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得△>0,考查了推理能力与计算能力,属于中档题.1年前查看全部
- 若直线l:y=kx+2与双曲线x23-y2=1恒有两个不同的交点A和B,且OA•OB>2(其中O为原点),求k的取值范围
若直线l:y=kx+
与双曲线2
-y2=1恒有两个不同的交点A和B,且x2 3
•OA
>2(其中O为原点),求k的取值范围.OB  medusa5181年前1
medusa5181年前1 -
 蝳娃娃 共回答了19个问题
蝳娃娃 共回答了19个问题 |采纳率94.7%解题思路:联立直线和双曲线方程,转化为一元二次方程,利用根与系数之间的关系即可求出k的取值范围.由将y=kx+
2代入双曲线
x2
3-y2=1消去y得(1-3k2)x2-6
2kx-9=0.
由直线l与双曲线交于不同的两点得
1−3k2≠0
△=(−6
2k)2+36(1−3k2)=36(1−k2)>0
即k2≠[1/3]且k2<1.①
设A(xA,yA),B(xB,yB),则xA+xB=
6
2k
1−3k2,xAxB=
−9
1−3k2.
由点评:
本题考点: 直线与圆锥曲线的关系.
考点点评: 本题主要考查直线和双曲线的位置关系,利用直线和双曲线联立转化为一元二次方程,利用根与系数之间的关系是解决本题的关键.1年前查看全部
- 若抛物线y2=2px的焦点与双曲线x23−y2=1的右焦点重合,则p的值为( )
若抛物线y2=2px的焦点与双曲线
−y2=1的右焦点重合,则p的值为( )x2 3
A.-4
B.4
C.-2
D.2 always-go-on1年前1
always-go-on1年前1 -
 hnrshbkj 共回答了17个问题
hnrshbkj 共回答了17个问题 |采纳率94.1%解题思路:根据双曲线方程可得它的右焦点坐标,结合抛物线y2=2px的焦点坐标([p/2],0),可得[p/2]=2,得p=4.∵双曲线
x2
3−y2=1中a2=3,b2=1
∴c=
a2+b2=2,得双曲线的右焦点为F(2,0)
因此抛物线y2=2px的焦点([p/2],0)即F(2,0)
∴[p/2]=2,即p=4
故选B点评:
本题考点: 抛物线的简单性质.
考点点评: 本题给出双曲线的焦点与抛物线焦点重合,求抛物线的焦参数,着重考查了双曲线的基本概念和抛物线的标准方程等知识,属于基础题.1年前查看全部
- 已知椭圆C:x2a2+y2b2=1(a>b>0)与双曲线x23-y2=1共焦点,点A(3,7)在椭圆C上.
已知椭圆C:
+x2 a2
=1(a>b>0)与双曲线y2 b2
-y2=1共焦点,点A(3,x2 3
)在椭圆C上.7
(1)求椭圆C的方程;
(2)已知点Q(0,2),P为椭圆C上的动点,点M满足:
=QM
,求动点M的轨迹方程.MP
 莱茵哈特vv1年前1
莱茵哈特vv1年前1 -
 中档球拍 共回答了13个问题
中档球拍 共回答了13个问题 |采纳率100%解题思路:(1)根据椭圆与双曲线公焦点,可知椭圆的焦点坐标,利用点A(3,
)在椭圆C上,根据椭圆的定义,我们可以求出a的值,根据焦点坐标,利用b2=a2-c2,可以求出b2,从而可求椭圆C的方程;7
(2)利用点M满足:
=QM
,可得动点M与动点P之间的坐标关系,利用点P满足椭圆方程,我们可以求出动点M的轨迹方程.MP (1)由已知得双曲线焦点坐标为F1(-2,0),F2(2,0),由椭圆的定义得|AF1|+|AF2|=2a,∴25+7+1+7=2a,∴a=32而c2=4,∴b2=a2-c2=18-4=14∴所求椭圆方程为x218+y214=1(2)设M(x,y),P(x0,y0),由QM=MP得(...
点评:
本题考点: 椭圆的标准方程;轨迹方程.
考点点评: 本题的考点是椭圆的标准方程,考查待定系数法求椭圆的标准方程,考查代入法求轨迹方程,解题的关键是利用向量关系,寻求动点之间的坐标关系.1年前查看全部
- (2013•和平区二模)已知双曲线x23−y2=1的左、右焦点分别为F1、F2,点P在双曲线上,且PF2⊥x轴,则F2到
(2013•和平区二模)已知双曲线
−y2=1的左、右焦点分别为F1、F2,点P在双曲线上,且PF2⊥x轴,则F2到直线PF1的距离为x2 3 [4/7][4/7]. hbver_1年前1
hbver_1年前1 -
 h54852 共回答了22个问题
h54852 共回答了22个问题 |采纳率95.5%解题思路:依题意,可求得点P的坐标,继而可求得直线PF1的方程,利用点到直线间的距离公式即可求得答案.∵F1、F2分别为双曲线
x2
3-y2=1的左、右焦点,
∴F1(-2,0),F2(2,0);
又点P在双曲线上,且PF2⊥x轴,
∴点P的横坐标为2,纵坐标y0=±
4
3−1=±
3
3.
∴P(2,±
3
3).
∴直线PF1的方程为:
3x±12y+2
3=0.
∴F2到直线PF1的距离d=
|
3×2±12×0+2
3|
7点评:
本题考点: 双曲线的简单性质.
考点点评: 本题考查双曲线的简单性质,考查直线的方程的确定与点到直线间的距离,求得直线PF1的方程是关键,考查分析与运算能力,属于中档题.1年前查看全部
- 双曲线x23-y24=1的两条准线间的距离为 ___ .
 dduron1年前1
dduron1年前1 -
 烟头Dream人 共回答了15个问题
烟头Dream人 共回答了15个问题 |采纳率93.3%解题思路:利用双曲线的标准方程即可得出准线.由双曲线
x2
3-
y2
4=1的可得:a2=3,b2=4,∴c2=a2+b2=7,
∴两条准线方程分别为x=±
a2
c,即x=±
3
7,化为x=±
3
7
7.
故两条准线之间的距离=2×
3
7
7=
6
7
7.
故答案为
6
7
7.点评:
本题考点: 双曲线的简单性质.
考点点评: 熟练掌握双曲线的标准方程及其性质是解题的关键.1年前查看全部
- 抛物线y2=2px的准线经过双曲线x23−y2=1的左焦点,则p=______.
 wangttyy1年前0
wangttyy1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 过双曲线x23-y24=1的焦点且与x轴垂直的弦长为___.
 爱吉吉1年前0
爱吉吉1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 已知椭圆与双曲线x23−y2=1有共同的焦点,且过点P(2,3),求双曲线的渐近线及椭圆的方程.
 Jasonps1年前1
Jasonps1年前1 -
 蓝蓝扬 共回答了18个问题
蓝蓝扬 共回答了18个问题 |采纳率88.9%解题思路:先把曲线的标准标准方程,其渐近线方程是
−y2=0,整理后就得到双曲线的渐近线方程.利用椭圆与双曲线有共同的焦点F1(-2,0),F2(2,0),设出椭圆方程,再利用点P(2,3)适合椭圆方程,就可求出椭圆的方程.x2 3 双曲线的标准形式为
x2
3−y2=1,
其渐近线方程是
x2
3−y2=0,
整理得双曲线的渐近线为:x±
3y=0.
由共同的焦点F1(-2,0),F2(2,0),可设椭圆方程为
y2
a2+
x2
b2=1,
点P(2,3)在椭圆上,
4
a2+
9
b2=1
a 2−b 2=4,
∴a2=16,b2=12,
所以椭圆方程为:
y2
16+
x2
12=1.点评:
本题考点: 圆锥曲线的共同特征.
考点点评: 本题考查本题考查双曲线的标准方程,以及椭圆的标准方程的求法,令标准方程中的“1”为“0”即可求出渐近线方程.在求双曲线与椭圆的标准方程时,一定要先分析焦点所在位置,再设方程,避免出错.1年前查看全部
- 椭圆x26+y22=1和双曲线x23-y2=1的公共焦点为F1,F2,P是两曲线的一个交点,那么cos∠F1PF2的值是
椭圆
+x2 6
=1和双曲线y2 2
-y2=1的公共焦点为F1,F2,P是两曲线的一个交点,那么cos∠F1PF2的值是( )x2 3
A. [1/3]
B. [2/3]
C. [7/3]
D. [1/4] 烟烟1191年前0
烟烟1191年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 顶点在原点且以双曲线x23−y2=1的右准线为准线的抛物线方程是______.
 麻兜兜1年前0
麻兜兜1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- (2013•江西)抛物线x2=2py(p>0)的焦点为F,其准线与双曲线x23-y23=1相交于A,B两点,若△ABF为
(2013•江西)抛物线x2=2py(p>0)的焦点为F,其准线与双曲线
-x2 3
=1相交于A,B两点,若△ABF为等边三角形,则p=______.y2 3  风一样的劳尔1年前1
风一样的劳尔1年前1 -
 紫茎微兰 共回答了11个问题
紫茎微兰 共回答了11个问题 |采纳率90.9%解题思路:求出抛物线的焦点坐标,准线方程,然后求出抛物线的准线与双曲线的交点坐标,利用三角形是等边三角形求出p即可.抛物线的焦点坐标为(0,[p/2]),准线方程为:y=-[p/2],
准线方程与双曲线联立可得:
x2
3-
(-
p
2)2
3=1,
解得x=±
3+
p2
4,
因为△ABF为等边三角形,所以
p2+x2=2|x|,即p2=3x2,
即p2=3(3+
p2
4),解得p=6.
故答案为:6.点评:
本题考点: 抛物线的简单性质;双曲线的简单性质.
考点点评: 本题考查抛物线的简单性质,双曲线方程的应用,考查分析问题解决问题的能力以及计算能力.1年前查看全部
- 若抛物线y2=2px的焦点与双曲线x23−y2=1的右焦点重合,则p的值为( )
若抛物线y2=2px的焦点与双曲线
−y2=1的右焦点重合,则p的值为( )x2 3
A. -4
B. 4
C. -2
D. 2 都市小农1年前1
都市小农1年前1 -
 rubywd 共回答了18个问题
rubywd 共回答了18个问题 |采纳率94.4%解题思路:根据双曲线方程可得它的右焦点坐标,结合抛物线y2=2px的焦点坐标([p/2],0),可得[p/2]=2,得p=4.∵双曲线
x2
3−y2=1中a2=3,b2=1
∴c=
a2+b2=2,得双曲线的右焦点为F(2,0)
因此抛物线y2=2px的焦点([p/2],0)即F(2,0)
∴[p/2]=2,即p=4
故选B点评:
本题考点: 抛物线的简单性质.
考点点评: 本题给出双曲线的焦点与抛物线焦点重合,求抛物线的焦参数,着重考查了双曲线的基本概念和抛物线的标准方程等知识,属于基础题.1年前查看全部
- 椭圆x26+y22=1和双曲线x23-y2=1的公共焦点为F1,F2,P是两曲线的一个交点,那么cos∠F1PF2的值是
椭圆
+x2 6
=1和双曲线y2 2
-y2=1的公共焦点为F1,F2,P是两曲线的一个交点,那么cos∠F1PF2的值是( )x2 3
A. [1/3]
B. [2/3]
C. [7/3]
D. [1/4] 不世之功q1年前0
不世之功q1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
大家在问
- 1do使用在单三人称形式还是非单三人称形式.单三人称形式的人称代词有哪些?
- 2填空题 一什么天地在括号里填量词,一( )天地.知道的请回答.我现在急!
- 3铁锅放置很长时间,完全生锈了,该怎么办?
- 4课外阅读是提高语文素养的重要途径.读__________我们可以_____________
- 5谁能帮我翻译一下这个句子“无论你去什么地方,都有要必要了解天气情况” 翻成英语谢谢了,大神帮忙啊
- 6On October 3rd to 4th,
- 7试确定有n位数码全是奇数,是1与3都出现正偶数次的数码个数.
- 8上帝的错误 作文
- 912*13*14*15*16*17
- 10过m边形的一个顶点有7条对角线,n边形没有对角线,K边形有2条对角线,则(m-k)=?
- 11谁知道电路里一些字母代表的意思,比如kw-h千瓦时 w功率 就是这样的字母,谁能说的清楚一点.
- 12现有两根长度分别为4cm和2cm的小木棒,请再找一根小木棒,以这三根木棒为边围成一个三角形,则第三根小木棒的长度可以是
- 13What's the man____?I don't know
- 14高中数学有一个c上面一个数下面一个数那个怎么算
- 1524除以(六分之五加八分之七) 二十五分之十八乘四加二十五分之二十一乘十八
