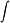微分方程y″+y=x2+1+sinx的特解形式可设为( )
 txqacf7_oq4f202022-10-04 11:39:541条回答
txqacf7_oq4f202022-10-04 11:39:541条回答A.y*=ax2+bx+c+x(Asinx+Bcosx)
B.y*=x(ax2+bx+c+Asinx+Bcosx)
C.y*=ax2+bx+c+Asinx
D.y*=ax2+bx+c+Acosx

已提交,审核后显示!提交回复
共1条回复
 xiaofanzi0107 共回答了24个问题
xiaofanzi0107 共回答了24个问题 |采纳率83.3%- 解题思路:由线性微分方程解的性质,利用待定系数法确定微分方程的特解形式.
对应齐次方程 y″+y=0 的特征方程为 λ2+1=0,
特征根为 λ=±i.
由线性微分方程解的性质可得,
如果y1 是微分方程 y″+y=x2+1 的解,
且y2 是微分方程 y″+y=sinx 的解,
则 y1+y2 是原微分方程的解.
对于微分方程 y″+y=x2+1=e0(x2+1)而言,因为 0不是特征根,
从而其特解形式可设为
y*1=ax2+bx+C.
对于微分方程 y″+y=sinx 而言,因为 i 为单重特征根,
从而其特解形式可设为
y*2=x(Asinx+Bcosx).
从而,可设原微分方程的特解形式可设为
y*=
y*1+
y*2=ax2+bx+C+x(Asinx+Bcosx).
故选:A.点评:
本题考点: 二阶常系数非齐次线性微分方程求解;线性微分方程解的性质及解的结构定理.
考点点评: 本题是一个基础型题目,难度系数不大,综合考察了线性微分方程的性质以及二阶非齐次线性微分方程的求解方法. - 1年前
相关推荐
- 如何求微分方程y〃+4y′+4y=2e^-2x的通解?
 tianxyu1年前1
tianxyu1年前1 -
 达到地极 共回答了12个问题
达到地极 共回答了12个问题 |采纳率91.7%对应齐次y〃+4y′+4y=0的特征值r1=r2=-2
所以齐次通解y1=(C1+C2x)e^(-2x)
采用微分算子法,原方程特解y2=[1/(D^2+4D+4)]*(2e^-2x)=(x^2)*e^(-2x)
通解y=y1+y21年前查看全部
- 微分方程y′sinx=ylny满足初始条件(当x=π/2时y=e)下的特解是?最好写出解题步骤
 redink20071年前2
redink20071年前2 -
 yanyeya 共回答了14个问题
yanyeya 共回答了14个问题 |采纳率85.7%(dy/dx)sinx=ylny
dy/ylny=sinxdx
d(lny)lny=sinxdx
d(二分之一lny的平方)=-d(cosx)
原函数为:(lny)的平方=-2cosx+C
当x=π/2时y=e,则C=1
所以原函数::(lny)的平方=-2cosx+11年前查看全部
- 求微分方程y′+ycosx=(lnx)e-sinx的通解.
 gg的草莓1年前3
gg的草莓1年前3 -
 hxldddd 共回答了16个问题
hxldddd 共回答了16个问题 |采纳率100%1年前查看全部
- 微分方程y′+xy=0的通解是______.
 逐鹿问鼎中原1年前1
逐鹿问鼎中原1年前1 -
 郁闷中的欣 共回答了20个问题
郁闷中的欣 共回答了20个问题 |采纳率90%解题思路:将微分方程,分离变量,两边积分,即可求解出来.由微分方程,得
dy
y=−xdx(y≠0)
两边积分,得
ln|y|=−
1
2x2+C1
∴y=Ce−
1
2x2,其中C=±eC1≠0
但y=0也是方程的解,
故微分方程y′+xy=0的通解是
y=Ce−
1
2x2,C为任意常数.点评:
本题考点: 可分离变量微分方程的求解.
考点点评: 此题考查了分离变量微分方程的解法,这是基础知识点,要熟练掌握.1年前查看全部
- 微分方程y′+ytanx=cosx的通解为y=______.
 quedong1年前0
quedong1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 求微分方程y″(x+y′2)=y′满足初始条件y(1)=y′(1)=1的特解.
 sellia11年前1
sellia11年前1 -
 8969313 共回答了21个问题
8969313 共回答了21个问题 |采纳率85.7%解题思路:本题为f(y″,y′,x)=0型二阶微分方程,通过p=y′降阶,转为可分离变量方程,求得p即y′,再求一次可分离变量方程即可.设y′=p,则原方程变为:
p′(x+p2)=p,
即:
[dp/dx(x+p2)=p,
化作:
x+p2
p=
dx
dp],
即:[dx/dp=
x
p+p
令
x
p=u,则x=up,
有:
dx
dp=u+p
du
dp]
所以:u+p
du
dp=u+p,
得:[du/dp=1,
所以:u=p+c,c为任意常数,
则:
x
p=p+c,
又因为y′(1)=1,
即:x=1时,p=1,
所以:c=0,
从而:x=p2
则:p=
x],
y′=
x
求得:y=
2
3x
3
2+C,C为任意常数,
因为:y(1)=1,
所以,C=[1/3],
于是,y=
2
3x
3
2+
1
3.点评:
本题考点: 可降阶的高阶微分方程求解.
考点点评: 本题考查可降阶的高阶微分方程的求解.需要注意灵活选定自变量、因变量,以便于求解为原则.1年前查看全部
- 若二阶常系数线性齐次微分方程y″+ay′+by=0的通解为y=(C1+C2x)ex,则非齐次方程y″+ay′+by=x满
若二阶常系数线性齐次微分方程y″+ay′+by=0的通解为y=(C1+C2x)ex,则非齐次方程y″+ay′+by=x满足条件y(0)=2,y′(0)=0的解为y=______.
 12HELEN1年前2
12HELEN1年前2 -
 linjingsoft 共回答了27个问题
linjingsoft 共回答了27个问题 |采纳率88.9%解题思路:由齐次微分方程解的形式,求出其对应的特征方程,确定a、b的值;然后利用待定系数法求出非齐次方程的一个特解,并利用线性微分方程解的结构写出通解;最后利用初值条件确定系数,求出满足题意的特解.因为常系数线性齐次微分方程y″+ay′+by=0 的通解为
y=(C1+C2 x)ex,
故 r1=r2=1为其特征方程的重根,且其特征方程为
(r-1)2=r2-2r+1,
故 a=-2,b=1.
对于非齐次微分方程为y″-2y′+y=x,
设其特解为 y*=Ax+B,
代入y″-2y′+y=x 可得,
0-2A+(Ax+B)=x,
整理可得
(A-1)x+(B-2A)=0,
所以 A=1,B=2.
所以特解为 y*=x+2,
通解为 y=(C1+C2 x)ex +x+2.
将y(0)=2,y(0)=0 代入可得,
C1=0,C2=-1.
故所求特解为 y=-xex+x+2.
故答案为-xex+x+2.点评:
本题考点: 二阶常系数齐次线性微分方程求解;微分方程的显式解、隐式解、通解和特解.
考点点评: 本题是一个中档型题目,考察了线性常微分方程的求解方法.题目的难度系数并不大,只是计算量较大.1年前查看全部
- 解微分方程y′′=1/(1+x²)
 lix200001年前2
lix200001年前2 -
 茜子泪 共回答了18个问题
茜子泪 共回答了18个问题 |采纳率94.4%y′′=1/(1+x²)
所以
y'=arctanx+c1
y=∫arctanxdx+c1x+c2
=xarctanx-∫x/(1+x²)dx+c1x+c2
=xarctanx-1/2ln(1+x²)+c1x+c21年前查看全部
- 微分方程y″+4y′+4y=0的通解为______.
 fleeaway1年前1
fleeaway1年前1 -
 sdfsduifg 共回答了20个问题
sdfsduifg 共回答了20个问题 |采纳率90%解题思路:首先将其特征根求出来,然后写出通解即可.由微分方程y″+4y′+4y=0的特征方程为:
r2+4r+4=0
解得:r1,2=-2
∴通解为:
y=(C1+C2x)e-2x,其中C1、C2为任意常数.点评:
本题考点: 二阶常系数齐次线性微分方程求解.
考点点评: 此题考查二阶常系数齐次线性方程组的解法,是基础知识点.1年前查看全部
- 微分方程y″+6y′+9y=0的通解y=______.
 GOGO8011年前1
GOGO8011年前1 -
 yanlin010 共回答了20个问题
yanlin010 共回答了20个问题 |采纳率95%解题思路:首先求解其特征方程,得到特征根的值;然后利用线性微分方程解的结构定理写出方程的通解.微分方程y″+6y′+9y=0的特征方程为:
λ2+6λ+9=0,
求解可得,λ1,2=-3,
从而方程的两个线性无关的解为:e-3x,xe-3x.
由二阶齐次线性微分方程解的结构定理可得,
所求方程的通解为:
y=C1e-3x+C2xe-3x.
故答案为:C1e-3x+C2xe-3x.点评:
本题考点: 线性微分方程解的性质及解的结构定理.
考点点评: 本题考查了二阶齐次线性微分方程的求解方法,其中利用了线性微分方程解的结构定理,题目的难度系数适中.1年前查看全部
- 求微分方程y″(x+y′2)=y′满足初始条件y(1)=y′(1)=1的特解.
 捣蒜当家kk1年前1
捣蒜当家kk1年前1 -
 chao_shikong 共回答了19个问题
chao_shikong 共回答了19个问题 |采纳率94.7%解题思路:本题为f(y″,y′,x)=0型二阶微分方程,通过p=y′降阶,转为可分离变量方程,求得p即y′,再求一次可分离变量方程即可.设y′=p,则原方程变为:
p′(x+p2)=p,
即:
[dp/dx(x+p2)=p,
化作:
x+p2
p=
dx
dp],
即:[dx/dp=
x
p+p
令
x
p=u,则x=up,
有:
dx
dp=u+p
du
dp]
所以:u+p
du
dp=u+p,
得:[du/dp=1,
所以:u=p+c,c为任意常数,
则:
x
p=p+c,
又因为y′(1)=1,
即:x=1时,p=1,
所以:c=0,
从而:x=p2
则:p=
x],
y′=
x
求得:y=
2
3x
3
2+C,C为任意常数,
因为:y(1)=1,
所以,C=[1/3],
于是,y=
2
3x
3
2+
1
3.点评:
本题考点: 可降阶的高阶微分方程求解.
考点点评: 本题考查可降阶的高阶微分方程的求解.需要注意灵活选定自变量、因变量,以便于求解为原则.1年前查看全部
- 求微分方程y′+ycosx=(lnx)e-sinx的通解.
 顽石小祖儿1年前1
顽石小祖儿1年前1 -
 passion_2008 共回答了16个问题
passion_2008 共回答了16个问题 |采纳率93.8%1年前查看全部
- 设y1,y2,y3是微分方程y″+py′+qy=f(x)的三个线性无关的解,c1,c2为任意常数,则y=c1y1+c2y
设y1,y2,y3是微分方程y″+py′+qy=f(x)的三个线性无关的解,c1,c2为任意常数,则y=c1y1+c2y2+(1-c1-c2)y3( )
A.是此方程的解,但不一定是它的通解
B.不是此方程的解
C.是此方程的特解
D.是此方程的通解 志远心高1年前1
志远心高1年前1 -
 xiaobudai 共回答了16个问题
xiaobudai 共回答了16个问题 |采纳率93.8%解题思路:将y=c1y1+c2y2+(1-c1-c2)y3变形,然后根据微分方程解的结构的相关性质,就可以选出答案.∵y1,y2,y3是微分方程y″+py′+qy=f(x)的三个线性无关的解,
∴y1-y3和y2-y3是其对应齐次微分方程y″+py′+qy=0的两个线性无关的解,
又∵y=c1y1+c2y2+(1-c1-c2)y3=c1(y1-y3)+c2(y2-y3)+y3,其中c1,c2两个独立的任意常数,
∴y=c1y1+c2y2+(1-c1-c2)y3是微分方程y″+py′+qy=f(x)的通解,
故选:D.点评:
本题考点: 微分方程的显式解、隐式解、通解和特解.
考点点评: “二阶非齐次线性微分方程的通解=二阶对应齐次微分方程的通解+二阶非齐次线性微分方程的一特解”,这一结论,跟线性代数中线性方程组解的结构相同.1年前查看全部
- 若二阶常系数线性齐次微分方程y″+ay′+by=0的通解为y=(c1+c2x)ex,
若二阶常系数线性齐次微分方程y″+ay′+by=0的通解为y=(c1+c2x)ex,
则非齐次方程y″+ay′+by=x满足条件y(0)=0,y′(0)=0的解为:y=(
−a b2
x)ex+a+b b2
x−1 b a b2 (.
−a b2
x)ex+a+b b2
x−1 b a b2  山里的孩子王1年前1
山里的孩子王1年前1 -
 cq1cdv 共回答了16个问题
cq1cdv 共回答了16个问题 |采纳率87.5%解题思路:求得非齐次方程的特解,则可得到非齐次方程的通解=齐次方程的通解+非齐次方程的特解,代入初始条件,即可得到特解.非齐次微分方程y″+ay′+by=x对应的齐次微分方程y″+ay′+by=0的通解为:
Y=(c1+c2x)ex,
故可设非齐次微分方程y″+ay′+by=x的特
y*=mx+n,
y*′=m,y*″=0,
代入非齐次微分方程:y″+ay′+by=x,
可得:am+b(mx+n)=x,
从而:m=
1
b,n=−
a
b2,
所以:y*=
1
bx−
a
b2
于是,非齐次微分方程y″+ay′+by=x的通
y=Y+y*=(c1+c2x)ex+
1
bx−
a
b2,
又由:y(0)=0,y′(0)=0可得:
c1−
a
b2=0
c1+c2+
1
b=0,
所以求得:
c1=
a
b2
c2=−
a+b
b2,
所以,y=(
a
b2−
a+b
b2x)ex+
1
bx−
a
b2.点评:
本题考点: 二阶常系数齐次线性微分方程求解;二阶常系数非齐次线性微分方程求解.
考点点评: 本题考查二阶常系数非齐次微分方程的求解.需注意本题非齐次方程满足的条件代入时要代非齐次方程的通解而不是特解.1年前查看全部
- 求微分方程y′cosy=(1+cosxsiny)siny
求微分方程y′cosy=(1+cosxsiny)siny
前边那个次y也是方程中的 人世走一回1年前1
人世走一回1年前1 -
 583_77 共回答了26个问题
583_77 共回答了26个问题 |采纳率100%两边分别求导cosy'=siny'+cosysinysiny' 展开~
自己再算就出来了1年前查看全部
- 求微分方程y′+xy′2-y=0的直线积分曲线.
求微分方程y′+xy′2-y=0的直线积分曲线.
我是一个初学者,请说简单点, shoegazer071年前1
shoegazer071年前1 -
 洛水星语 共回答了26个问题
洛水星语 共回答了26个问题 |采纳率84.6%xy′2是什么意思1年前查看全部
- 求微分方程y″+y=cosx的通解.
 wshcr88881年前2
wshcr88881年前2 -
 猪头上的小酒窝 共回答了17个问题
猪头上的小酒窝 共回答了17个问题 |采纳率94.1%解题思路:先求对应齐次方程的通解,然后求原方程特解,即可求出.原方程对应齐次方程y''+y=0的特征方程为:
r2+1=0,其特征根为:
r1=i,r2=-i,
所以齐次方程的通解为:
y=C1cosx+C2sinx.
设非齐次方程y''+y=cosx的一个特解为:
y2=Excosx+Dxsinx,代入该方程,得E=0,D=
1
2.
所以y2=
1
2xsinx.
所以原方程的通解为y=C1cosx+C2sinx+
1
2xsinx.点评:
本题考点: 齐次方程求解.
考点点评: 本题主要考查齐次方程的求解,属于基础题.1年前查看全部
- 求微分方程y·=1/x(y+xlnx)满足初始条件y|x=0 =0的特解.
 tony19831191年前2
tony19831191年前2 -
 以朋友的名义 共回答了15个问题
以朋友的名义 共回答了15个问题 |采纳率93.3%y'=1/x(y+xlnx)
y'=y/x+lnx
设u=y/x,y=ux,y'=u'x+u
u'x+u=u+lnx
u'=lnx/x
u=∫lnx/x·dx=∫lnxd(lnx)=(lnx)^2/2+C
y=ux=[(lnx)^2/2+C]x=x(lnx)^2/2+Cx
从原方程及通解来看x取不到0,初始条件是不是y|x=1 =0?
如果x=1时y=0
0=0+C·1,C=0
特解为y=x(lnx)^2/21年前查看全部
- 求微分方程y〃+2y′=x的通解
 eunicewu1年前2
eunicewu1年前2 -
 帆影旋 共回答了30个问题
帆影旋 共回答了30个问题 |采纳率93.3%先解特征方程
λ²+2λ=0
得到λ=-2 或者 λ=0
再找一个特解
方程有 形入Ax²+Bx的特解
代入有 (2A+2B)+4Ax=x 所以 4A=1,2A+2B=0
得到A=1/4 B=-1/4,得到特解 x²/4-x/4
所以通解为y= C1e ^(-2x)+C2+x²/4-x/41年前查看全部
- 若二阶常系数线性齐次微分方程y″+ay′+by=0的通解为y=(C1+C2x)ex,则非齐次方程y″+ay′+by=x满
若二阶常系数线性齐次微分方程y″+ay′+by=0的通解为y=(C1+C2x)ex,则非齐次方程y″+ay′+by=x满足条件y(0)=2,y′(0)=0的解为y=______.
 qqzhangjin1年前1
qqzhangjin1年前1 -
 我衣彩 共回答了16个问题
我衣彩 共回答了16个问题 |采纳率87.5%解题思路:由齐次微分方程解的形式,求出其对应的特征方程,确定a、b的值;然后利用待定系数法求出非齐次方程的一个特解,并利用线性微分方程解的结构写出通解;最后利用初值条件确定系数,求出满足题意的特解.因为常系数线性齐次微分方程y″+ay′+by=0 的通解为
y=(C1+C2 x)ex,
故 r1=r2=1为其特征方程的重根,且其特征方程为
(r-1)2=r2-2r+1,
故 a=-2,b=1.
对于非齐次微分方程为y″-2y′+y=x,
设其特解为 y*=Ax+B,
代入y″-2y′+y=x 可得,
0-2A+(Ax+B)=x,
整理可得
(A-1)x+(B-2A)=0,
所以 A=1,B=2.
所以特解为 y*=x+2,
通解为 y=(C1+C2 x)ex +x+2.
将y(0)=2,y(0)=0 代入可得,
C1=0,C2=-1.
故所求特解为 y=-xex+x+2.
故答案为-xex+x+2.点评:
本题考点: 二阶常系数齐次线性微分方程求解;微分方程的显式解、隐式解、通解和特解.
考点点评: 本题是一个中档型题目,考察了线性常微分方程的求解方法.题目的难度系数并不大,只是计算量较大.1年前查看全部
- 微分方程y″+6y′+9y=0的通解y=______.
 化作绕指柔1年前2
化作绕指柔1年前2 -
 落花2朵 共回答了20个问题
落花2朵 共回答了20个问题 |采纳率85%解题思路:首先求解其特征方程,得到特征根的值;然后利用线性微分方程解的结构定理写出方程的通解.微分方程y″+6y′+9y=0的特征方程为:
λ2+6λ+9=0,
求解可得,λ1,2=-3,
从而方程的两个线性无关的解为:e-3x,xe-3x.
由二阶齐次线性微分方程解的结构定理可得,
所求方程的通解为:
y=C1e-3x+C2xe-3x.
故答案为:C1e-3x+C2xe-3x.点评:
本题考点: 线性微分方程解的性质及解的结构定理.
考点点评: 本题考查了二阶齐次线性微分方程的求解方法,其中利用了线性微分方程解的结构定理,题目的难度系数适中.1年前查看全部
- 微分方程y″+2y′+3y=e-xcos2x的特解应具有形式( )
微分方程y″+2y′+3y=e-xcos
x的特解应具有形式( )2
A.e-x(acosx+bsinx)
B.e-xbxsinx+ae-xcosx
C.xe-x(acos
x+bsin2
x)2
D.e-x(acos
x+bsin2
x))2  dfwy88021年前1
dfwy88021年前1 -
 Mostarace 共回答了20个问题
Mostarace 共回答了20个问题 |采纳率85%解题思路:首先求出对应齐次微分方程的特征根,然后根据特征根和f(x)=e−xcos
x就可以确定特解的形式.2 由于微分方程y″+2y′+3y=e-xcos
2x所对应的特征方程为
r2+2r+3=0
解得:r1,2=−1±
2i
而f(x)=e−xcos
2x是属于eλx[Pl(x)cosωx+Pn(x)sinωx]型,这里λ=-1,ω=
2,Pl(x)=1,Pn(x)=0
而λ±ωi=-1±
2i是特征方程的根,因此微分方程的特解,可设为
y*=xe−x[acos
2x+bsin
2x]
故选:C.点评:
本题考点: 二阶常系数非齐次线性微分方程求解.
考点点评: 此题考查二阶常系数非齐次特解的求法,要根据方程右端的f(x)形式和特征根对应的关系来给出特解形式.1年前查看全部
- 求微分方程y′+2xy/(x^2+4)=0满足y(0)=1的特解.请单的写一下计算步骤,
 PJLdx1年前1
PJLdx1年前1 -
 厦门人200 共回答了18个问题
厦门人200 共回答了18个问题 |采纳率100%这个采用变量分离
dy/dx+2xy/(x²+4)=0
所以dy/y=-2xdx/(x²+4)=-d(x²+4)/(x²+4)
两边积分即可
lny=-ln(x²+4)+C
y(0)=1
所以C=ln4
代入化简即可得到
y=4/(x²+4)1年前查看全部
- 二阶非线性微分方程y〃=-ksiny
二阶非线性微分方程y〃=-ksiny
RT 山上一狼1年前0
山上一狼1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 求微分方程y″+[2/1-y]y′2=0的通解.
 johnsonjohn2k1年前1
johnsonjohn2k1年前1 -
 jasmine1111 共回答了20个问题
jasmine1111 共回答了20个问题 |采纳率90%解题思路:这是y″=f(y′,y)型的可降阶的微分方程,令y'=p,降为一次微分方程求解.令y'=p,则y″=p
dp
dy
∴p
dp
dy+
2
1-yp2=0
∴①当p≠0时,[dp/p=2
dy
y-1],两边积分,得
ln|p|=ln(y-1)2+ln|C1|
即p=C1(y-1)2,C1≠0
此时,
dy
dx=C1(y-1)2
解得
1
1-y=C1x+C2,C1≠0,C2为任意常数.
②当p=0时,此时y=C
综合①②得
微分方程的通解为:
1
1-y=C1x+C2,C1,C2为任意常数.点评:
本题考点: 可降阶的高阶微分方程求解
考点点评: 此题考查可降阶的微分方程的解法,属于基础知识点.1年前查看全部
- 求微分方程y″-y′-2y=(2x-5)e^2x的特解时,应设特解为什麼?
 hvz17b7jw79fa1年前1
hvz17b7jw79fa1年前1 -
 可可和果果的糖糖 共回答了17个问题
可可和果果的糖糖 共回答了17个问题 |采纳率100%y″-y′-2y=0的特征方程:r^2-r-2=0根为:2,-1
因为右端是e^2x,2是单根,故特解形式为y*=x(Ax+B)e^2x1年前查看全部
- 求微分方程y″+5y′=2x+e-5x的一个特解.
 鬼厉1101年前1
鬼厉1101年前1 -
 柳晓 共回答了15个问题
柳晓 共回答了15个问题 |采纳率100%解题思路:首先,将齐次方程的特征根通解求出来;然后将微分方程y″+5y′=2x+e-5x拆开成微分方程y″+y′=2x和微分方程y″+y′=e-5x,分别求这两者的特解;再相加即可得到答案.由于微分方程y″+5y′=2x+e-5x的特征方程为r2+5r=0,解得特征根为r=0、r=-5
因此y″+5y′=0通解为y=C1+C2e−5x
又微分方程y″+5y′=2x的f(x)=2x,其f(x)=2x,而λ=0是特征根,
故其特解为y1=x(ax+b),代入到微分方程y″+5y′=2x,解得a=
1
5,b=−
2
25
即y″+5y′=2x的特解为y1=
1
5x(x−
2
5)
又微分方程y″+5y′=e-5x的f(x)=e-5x,λ=-5是特征根
故其特解为y2=cxe−5x,代入到微分方程y″+5y′=e-5x,解得:c=−
1
5
即微分方程y″+5y′=e-5x的特解为y2=−
1
5xe−5x
∴微分方程y″+5y′=2x+e-5x的一个特解为y1+y2=
1
5x(x−
2
5)−
1
5xe−5x点评:
本题考点: 二阶常系数非齐次线性微分方程求解.
考点点评: 此题考查二阶常系数非齐次线性微分方程的求解,是基础知识点.需要注意的是,求特解时,将其拆开成两个微分方程的形式,分别求.1年前查看全部
- 求微分方程y′′+(y′)²=1满足y=|x=0=0,y′|x=0=0的特解.
 Aidimi1年前2
Aidimi1年前2 -
 83139091 共回答了26个问题
83139091 共回答了26个问题 |采纳率92.3%令z=y'
原方程变为
z'+z²=1
dz/dx=1-z²
dz/(1-z²)=dx
(1/2)[dz/(1-z)+dz/(1+z)]=dx
(1/2)ln|(1+z)/(1-z)|=x+C
代入x=0,z(0)=y'(0)=0
C=0
ln|(1+z)/(1-z)|=2x
(1+z)/(1-z)=e^(2x)
1+z=e^2x-e^2x z
z=(e^2x-1)/(e^2x+1)
y'=(e^2x-1)/(e^2x+1)=1-2/(e^2x +1)
积分
y=C+x-2积分 e^x dx/[e^x(e^2x+1)]
t=e^x,dt=e^xdx
y=C+x-2积分 dt/[t(t^2+1)]
=C+x-2积分 [dt/t-t dt /(t^2+1)]
=C+x-2ln |t|+ln|t^2+1|
=C+x-2x+ln(e^2x +1)
=C-x+ln(e^2x+1)
代入x=0,y(0)=0
C=-ln2
y=-ln2-x+ln(e^(2x)+1)1年前查看全部
- 微分方程y〃=1/xy′+xe∧x的通解是
 jrmmy1年前0
jrmmy1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 求微分方程y′′+(y′)∧2+1=0的通解
 hugo光1年前1
hugo光1年前1 -
 统筹学 共回答了18个问题
统筹学 共回答了18个问题 |采纳率94.4%x(y^2+1)dx+y(1-x^2)dy=0
y/(1+y²)dy=x/(x²-1)dx
即
2y/(1+y²)dy=2x/(x²-1)dx
两边积分,得
ln(1+y²)=ln(x²-1)+lnc
所以
通解为
1+y²=c(x²-1)1年前查看全部
- 求微分方程y〃+2y′+y=cos2x的通解
 大包爱麦兜1年前1
大包爱麦兜1年前1 -
 xiaomiaochen 共回答了17个问题
xiaomiaochen 共回答了17个问题 |采纳率94.1%看来没人回答了,还是我来吧!
用matlab求y=dsolve('D2y+2*Dy+y=cos(2*x)','x')
得:y=exp(-x)*C2+exp(-x)*x*C1-3/25*cos(2*x)+4/25*sin(2*x)1年前查看全部
- 求微分方程yˊ+2y=xe-x的通解
 emehhdahv1年前1
emehhdahv1年前1 -
 nsxs8fbyg7e89 共回答了23个问题
nsxs8fbyg7e89 共回答了23个问题 |采纳率100%先解齐次方程yˊ+2y=0,
再求特解,设y=(ax+b)e^(-x)
带回方程可以求出a=1,b=-1
最终 的通解就是齐次方程通解加非齐次方程特解.1年前查看全部
- 微分方程y″+2y′+y=xe-x的通解为y=(C1+C2x+16x3)e−xy=(C1+C2x+16x3)e−x.
 winzeng20071年前1
winzeng20071年前1 -
 cih2007 共回答了10个问题
cih2007 共回答了10个问题 |采纳率100%解题思路:首先,将对应齐次方程的特征根求出来;然后根据xe-x和特征根,求得其特解形式.由于特征方程为r2+2r+1=0,解得特征根为r=-1(2重)
∴齐次方程的通解为y=(C1+C2x)e−x
而f(x)=xe-x,λ=-1
故有特y*=x2(ax+b)e-x,
代入微分方程y″+2y′+y=xe-x,解得
a=
1
6,b=0
∴特解y*=
1
6x3e−x
∴通解为:
y=(C1+C2x+
1
6x3)e−x点评:
本题考点: 二阶常系数非齐次线性微分方程求解.
考点点评: 此题考查二阶常系数非齐次线性微分方程的求解,是基础知识点.1年前查看全部
- 求微分方程y′+ycosx=(lnx)e-sinx的通解.
 pgby1年前0
pgby1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 求微分方程y″+y=cosx的通解.
 沸点19801年前1
沸点19801年前1 -
 shy_0418 共回答了23个问题
shy_0418 共回答了23个问题 |采纳率95.7%解题思路:先求对应齐次方程的通解,然后求原方程特解,即可求出.原方程对应齐次方程y''+y=0的特征方程为:
r2+1=0,其特征根为:
r1=i,r2=-i,
所以齐次方程的通解为:
y=C1cosx+C2sinx.
设非齐次方程y''+y=cosx的一个特解为:
y2=Excosx+Dxsinx,代入该方程,得E=0,D=
1
2.
所以y2=
1
2xsinx.
所以原方程的通解为y=C1cosx+C2sinx+
1
2xsinx.点评:
本题考点: 齐次方程求解.
考点点评: 本题主要考查齐次方程的求解,属于基础题.1年前查看全部
- 求微分方程y′+ycosx=(lnx)e-sinx的通解.
 等待vs春天1年前0
等待vs春天1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
大家在问
- 1八减去五分之四除以十五分之二的差再被三分之二除商是多少
- 2知道特征向量和特征值如何求方阵
- 3使相同物质的量浓度的NaCl、MgCl2、AlCl3溶液中的Cl-离子完全沉淀时,若所用相同浓度的AgNO3溶液的体积比
- 4如何做好化学表格计算题中考在即,可化学表格计算题我还没能很好掌握,请提供表格题和解答过程,最重要的是提供解题技巧!
- 5“验证孟德尔分离定律中所选相对性状的显隐性一定易于区分”对吗这句话?
- 6坚持信念的英文怎么拼写
- 7一个长方体游泳池,长30厘米宽20厘米,深2米,如果放入900立方米的水,水面离游泳池的上沿有多少米?
- 8在△ABC中,DE‖BC,BE与CD相交于点P,且S△DBP=2S△DPE 求:S△ADE:S△ABC
- 9小学词语填空礼( )下士
- 10暮江吟谁写的
- 11麦克斯韦速率分布曲线左右面积相等的点
- 12如图示为研究二力平衡条件的实验装置,下列关于这个实验的叙述错误的是( ) A.为了减小摩擦,应选用尽量光滑的水平桌面
- 13初一上期第19课《月球上的足迹》的读一读,写一写的词语的意思是什么
- 14They all like _____ teacher,空格处是填them还是their?不是说动词加宾格的吗?(我们老
- 15有个问题请大家解答下。下面是HDU ACM 的题目链接http://acm.hdu.edu.cn/showproblem