x24+y23=1上有一动点P,圆E:(x-1)2+y2=1,过圆心E任意做一条直线与圆E交于A、B两点,圆F::(x+
 unfish2022-10-04 11:39:541条回答
unfish2022-10-04 11:39:541条回答| x2 |
| 4 |
| y2 |
| 3 |
| PA |
| PB |
| PC |
| PD |

已提交,审核后显示!提交回复
共1条回复
 蓝色月殿 共回答了23个问题
蓝色月殿 共回答了23个问题 |采纳率100%- 解题思路:先利用条件得出
与EA
互为相反向量,且长为1.再利用向量的三角形法则和向量的数量积的运算求出EB
•PA
的表达式;同理求出PB
•PC
,再与点P是椭圆上的点相结合即可求出结论.PD 设P(a,b)
则由已知得
EA与
EB互为相反向量,且长为1.
又∵
PA=
PE+
EA,
PB=
PE+
EB,
∴
PA•点评:
本题考点: 圆与圆锥曲线的综合.
考点点评: 本题主要考查向量基本知识以及圆与圆锥曲线的综合问题.是对知识点的一个综合考查,属于中档题. - 1年前
相关推荐
- 已知F1,F2为椭圆x24+y23=1的左、右焦点,M为椭圆上动点,有以下四个结论:
已知F1,F2为椭圆
+x2 4
=1的左、右焦点,M为椭圆上动点,有以下四个结论:y2 3
①|MF2|的最大值大于3;
②|MF1|•|MF2|的最大值为4;
③若过F2作∠F1MF2的外角平分线的垂线,垂足为N,则点N的轨迹方程是x2+y2=4;
④若动直线l垂直y轴,交此椭圆于A、B两点,P为l上满足|PA|•|PB|=2的点,则点P的轨迹方程为
+x2 2
=1或2y2 3
+x2 6
=1.2y2 9
以上结论正确的序号为______. hawkxhj1年前1
hawkxhj1年前1 -
 cn00241969 共回答了17个问题
cn00241969 共回答了17个问题 |采纳率100%解题思路:①利用椭圆的几何性质,求出|MF2|的最大值是a+c;②利用椭圆的几何性质|MF1|+|MF2|=2a,结合基本不等式MF1|•|MF2|≤(|MF1|+|MF2|2)2,求出|MF1|•|MF2|的最大值;③利用外角平分线作垂线的几何特征得出N是线段F2P的中点,结合中位线定理得ON的长为定值,从而求得N的轨迹方程;④设点P的坐标(x,y),依题意得A(x0,y),B(-x0,y),由|PA|•|PB|=2求出点P的坐标关系式,代入椭圆方程求出P点的轨迹方程.对于①,椭圆
x2
4+
y2
3=1中,a=2、c=1,∴|MF2|的最大值是a+c=2+1=3,∴①错误;
对于②,|MF1|+|MF2|=2a=4,∴|MF1|•|MF2|≤(
|MF1|+|MF2|
2)2=4,∴|MF1|•|MF2|的最大值为4,②正确;
对于③,如图,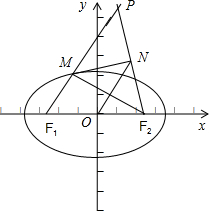
延长F2N与F1M交于P,连接ON,则点P、F2关于点N对称,
∴ON=[1/2]F1P=[1/2](MF1+MF2)=a=2,
∴动点N的轨迹方程为x2+y2=4;∴③正确;
对于④,设点P的坐标为(x,y),依题意得A(x0,y),B(-x0,y),
∵|PA|•|PB|=2,∴|x-x0|•|x+x0|=|x2-x02|=2,即x02=x2±2;
代入椭圆方程得
x2±2
4+
y2
3=1,
即
x2
2+
2y2
3=1(-
3≤y≤
3)与
x2
6+
2y2
9=1(-
3≤y≤
3);
∴P点的轨迹为两椭圆
x2
2+
2y2
3=1与
x2
6+
2y2
9=1夹在两直线y=±
3之间的弧长,∴④错误;
综上,正确的命题是②③.
故答案为:②③.点评:
本题考点: 命题的真假判断与应用.
考点点评: 本题考查了椭圆方程的定义与几何性质的综合应用问题,也考查了一定的推理与计算能力,是综合题,也是较难的题目.1年前查看全部
- (2013•南充三模)P点在椭圆x24+y23=1上运动,Q,R分别在两圆(x+1)2+y2=1和(x-1)2+y2=1
(2013•南充三模)P点在椭圆
+x2 4
=1上运动,Q,R分别在两圆(x+1)2+y2=1和(x-1)2+y2=1上运动,则|PQ|+|PR|的最大值为______.y2 3  烧成灰1年前0
烧成灰1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 设椭圆x24+y23=1的长轴两端点为M、N,点P在椭圆上,则PM与PN的斜率之积为( )
设椭圆
+x2 4
=1的长轴两端点为M、N,点P在椭圆上,则PM与PN的斜率之积为( )y2 3
A. −3 4
B. −4 3
C. [3/4]
D. [4/3] caoase1年前0
caoase1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- F1、F2为椭圆x24+y23=1的左、右焦点,A为椭圆上任一点,过焦点F1向∠F1AF2的外角平分线作垂线,垂足为D,
F1、F2为椭圆
+x2 4
=1的左、右焦点,A为椭圆上任一点,过焦点F1向∠F1AF2的外角平分线作垂线,垂足为D,则点D的轨迹方程是 ___ .y2 3
 A家徒四壁A1年前0
A家徒四壁A1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 已知抛物线的顶点是椭圆C:x24+y23=1的中心O,焦点与该椭圆的右焦点重合.
已知抛物线的顶点是椭圆C:
+x2 4
=1的中心O,焦点与该椭圆的右焦点重合.y2 3
(Ⅰ)求抛物线的方程;
(Ⅱ)设椭圆C的右准线交x轴于点Q,过点Q的直线l交抛物线于D、E两点.求△ODE面积的最小值;
(Ⅲ)设A、B分别为椭圆C的左、右顶点,P为右准线上不同于点Q的任意一点,若直线AP、BP分别与椭圆相交于异于A、B的点M、N.求证:点B在以MN为直径的圆内. 妖之蓝雨1年前0
妖之蓝雨1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 在平面直角坐标系xOy中,已知椭圆x24+y23=1的左焦点为F,直线x-y-1=0,x-y+1=0与椭圆分别相交于点A
在平面直角坐标系xOy中,已知椭圆
+x2 4
=1的左焦点为F,直线x-y-1=0,x-y+1=0与椭圆分别相交于点A,B,C,D,则AF+BF+CF+DF=______.y2 3  bwsq123561年前1
bwsq123561年前1 -
 天空里的云彩 共回答了20个问题
天空里的云彩 共回答了20个问题 |采纳率100%解题思路:利用直线过椭圆的焦点,转化为椭圆的定义,即可求得结论.由题意,设椭圆的右焦点为F1,两条平行直线分别经过椭圆的两个焦点,连接AF,F1D.
由椭圆的对称性可知,四边形AFDF1(其中F1是椭圆的左焦点)为平行四边形,所以AF1=FD,同理BF1=CF
所以AF+BF+CF+DF=AF+BF+BF1+AF1=4a=8.
故答案为:8.点评:
本题考点: 椭圆的简单性质.
考点点评: 本题主要考查了椭圆的方程和椭圆的性质,考查椭圆的定义,属于基础题.1年前查看全部
- 椭圆x24+y23=1的左焦点为F,直线x=m与椭圆相交于点A、B,当△FAB的周长最大时,△FAB的面积是( )
椭圆
+x2 4
=1的左焦点为F,直线x=m与椭圆相交于点A、B,当△FAB的周长最大时,△FAB的面积是( )y2 3
A. [1/2]
B. 2
C. [1/3]
D. 3 不再失忆1年前0
不再失忆1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 若直线mx+ny=4和⊙O:x2+y2=4相交,则点P(m,n)与椭圆C:x24+y23=1的位置关系为( )
若直线mx+ny=4和⊙O:x2+y2=4相交,则点P(m,n)与椭圆C:
+x2 4
=1的位置关系为( )y2 3
A.点P在椭圆C内
B.点P在椭圆C上
C.点P在椭圆C外
D.以上三种均有可能 candicess1年前1
candicess1年前1 -
 忆纷飞1357 共回答了11个问题
忆纷飞1357 共回答了11个问题 |采纳率90.9%解题思路:由于直线mx+ny=4和⊙O:x2+y2=4相交,可得圆心(0,0)到直线的距离d<r.即4m2+n2<2,得到m2>4-n2.进而得到m24+n23>4−n24+n23=1+n212>1,即可判断出位置关系.∵直线mx+ny=4和⊙O:x2+y2=4相交,∴圆心(0,0)到直线的距离d<r.
∴
4
m2+n2<2,化为m2+n2>4.
∴m2>4-n2.
∵
m2
4+
n2
3>
4−n2
4+
n2
3=1+
n2
12>1,
∴点P(m,n)在椭圆C:
x2
4+
y2
3=1的外部.
故选:C.点评:
本题考点: 直线与圆锥曲线的关系.
考点点评: 本题考查了直线与圆的位置关系、点与椭圆的位置关系、点到直线的距离公式,属于中档题.1年前查看全部
- 已知动点A、B分别在图中抛物线y2=4x及椭圆x24+y23=1的实线上运动,若AB∥x轴,点N的坐标为(1,0),则三
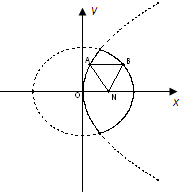 已知动点A、B分别在图中抛物线y2=4x及椭圆
已知动点A、B分别在图中抛物线y2=4x及椭圆
+x2 4
=1的实线上运动,若AB∥x轴,点N的坐标为(1,0),则三角形ABN的周长l的取值范围是( )y2 3
A.(3,4]
B.(3,4)
C.([10/3],4]
D.([10/3],4) songbeng1年前1
songbeng1年前1 -
 青枣科 共回答了19个问题
青枣科 共回答了19个问题 |采纳率84.2%解题思路:利用用抛物线的焦半径公式和椭圆的焦半径公式来解答,先通过联立抛物线与椭圆方程,求出A,B点的横坐标范围,再利用焦半径公式转换为以B点的横坐标为参数的式子,再根据前面求出的B点横坐标方位计算即可.由抛物线y2=4x及椭圆
x2
4+
y2
3=1可知,在第一象限的交点横坐标为[2/3],
设A(x1,y1),B(x2,y2),则0<x1<[2/3],[2/3]<x2<2,
由可得,三角形ABN的周长l=|AN|+|AB|+|BN|=x1+[p/2]+x2-x1+a-ex2=[p/2]+a+[1/2]x2=3+[1/2]x2,
∵[2/3]<x2<2,
∴[10/3]<3+[1/2]x2<4
故选D.点评:
本题考点: 抛物线的简单性质;椭圆的简单性质.
考点点评: 本题考查了抛物线与椭圆焦半径公式的应用,做题时要善于把未知转化为已知.1年前查看全部
- 设椭圆:x24+y23=1的长轴两端点为M、N,点P在椭圆上,则PM与PN的斜率之积为 ___ .
 雨中男子1年前0
雨中男子1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 若过椭圆C:X24+y23=1的左焦点F且倾斜角为45°的直线l与椭圆C交于A、B两点,则[1|AF|+1|BF|=(
若过椭圆C:
+X2 4
=1的左焦点F且倾斜角为45°的直线l与椭圆C交于A、B两点,则[1y2 3 |AF|  tcl_cxx1年前1
tcl_cxx1年前1 -
 小小仙女3 共回答了13个问题
小小仙女3 共回答了13个问题 |采纳率100%解题思路:先根据椭圆方程求得焦点坐标,进而设出直线l的方程,与椭圆方程联立消去y,设A(x1,y1),B(x2,y2),根据韦达定理求得x1•x2和x1+x2的值,进而根据直线方程求得y1y2的值,最后根据弦长公式求出|AB|,利用韦达定理求出|AF||BF|,即可求得答案.由
X2
4+
y2
3=1,得a2=4,b2=3,c2=a2-b2=1,左焦点为(-1,0).
则直线l的方程为y=x+1.
代入
X2
4+
y2
3=1,得7x2+8x-8=0,
设A(x1,y1),B(x2,y2),
则x1•x2=−
8
7,x1+x2=−
8
7,
y1y2=(x1+1)(x2+1)=x1x2+(x1+x2)+1=−
8
7−
8
7+1=−
9
7,
|AB|=
1+1
(−
8
7)2+
32
7=[24/7],
|AF||BF|=
(x1+1)2+ y12•
(x2+1)2+y22=2|y1y2|=[18/7]
∴[1
|AF|+
1
|BF|=
|AB|
|AF||BF|=
4/3]
故选A.点评:
本题考点: 椭圆的简单性质.
考点点评: 本题主要考查了椭圆的应用.当涉及过叫焦点的直线时,常需设出直线方程与椭圆方程联立利用韦达定理来解决.1年前查看全部
- F1、F2为椭圆x24+y23=1的左、右焦点,A为椭圆上任一点,过焦点F1向∠F1AF2的外角平分线作垂线,垂足为D,
F1、F2为椭圆
+x2 4
=1的左、右焦点,A为椭圆上任一点,过焦点F1向∠F1AF2的外角平分线作垂线,垂足为D,则点D的轨迹方程是 ___ .y2 3
 宛若白玉1年前0
宛若白玉1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 若P是椭圆x24+y23=1上的点,F1和F2是焦点,则k=|PF1|•|PF2|的最大值和最小值分别是______和_
若P是椭圆
+x2 4
=1上的点,F1和F2是焦点,则k=|PF1|•|PF2|的最大值和最小值分别是______和______.y2 3  aflyingcat1年前1
aflyingcat1年前1 -
 Jacqueswang 共回答了20个问题
Jacqueswang 共回答了20个问题 |采纳率90%解题思路:由题意,设|PF1|=x,故有|PF1|•|PF2|=x(4-x)=-x2+4x=-(x-2)2+4,确定x的范围,即可求得k的最值.由题意,设|PF1|=x,
∵|PF1|+|PF2|=2a=4,∴|PF2|=4-x
∴|PF1|•|PF2|=x(4-x)=-x2+4x=-(x-2)2+4
∵a=2,b=
3,∴c=
a2−b2=1
∴1≤x≤3
∴x=1或3时,k=-x2+4x取最小值3;x=2时,k=-x2+4x取最大值为4
故答案为:4,3.点评:
本题考点: 椭圆的简单性质.
考点点评: 本题以椭圆的标准方程为载体,考查椭圆定义的运用,考查函数的构建,考查函数的单调性,属于基础题.1年前查看全部
- 椭圆C:x24+y23=1的左、右顶点分别为A1、A2,点P在C上且直线PA2斜率的取值范围是[-2,-1],那么直线
椭圆C:
+x2 4
=1的左、右顶点分别为A1、A2,点P在C上且直线PA2斜率的取值范围是[-2,-1],那么直线y2 3
PA1斜率的取值范围是[[3/8],[3/4]][[3/8],[3/4]]. liaojp1年前1
liaojp1年前1 -
 脚后跟觉得 共回答了15个问题
脚后跟觉得 共回答了15个问题 |采纳率100%解题思路:由题意求A1、A2的坐标,设出点P的坐标,代入求斜率,进而求PA1斜率的取值范围.由椭圆的标准方程可知,
左右顶点分别为A1(-2,0)、A2(2,0),
设点P(a,b)(a≠±2),则
a2
4+
b2
3=1…①,KPA1=[b/a+2],KPA2=[b/a−2];
则KPA1KPA2=[b/a+2]•[b/a−2]=
b2
a2−4,
将①式代入得KPA1KPA2=-[3/4],
∵KPA2∈[-2,-1],
∴KPA1∈[[3/8],[3/4]].
故答案为:[[3/8],[3/4]].点评:
本题考点: 椭圆的简单性质.
考点点评: 本题考查了圆锥曲线的简单性质应用,同时考查了直线的斜率公式及学生的化简能力,属于基础题.1年前查看全部
- 点P是椭圆x24+y23=1外的任意一点,过点P的直线PA、PB分别与椭圆相切于A、B两点.
点P是椭圆
+x2 4
=1外的任意一点,过点P的直线PA、PB分别与椭圆相切于A、B两点.y2 3
(1)若点P的坐标为(1,2),求直线AB的方程.
(2)设椭圆的左焦点为F,请问:当点P运动时,∠PFA与∠PFB是否总是相等?若是,请给出证明. zhaowanxue88481年前1
zhaowanxue88481年前1 -
 朗仁 共回答了13个问题
朗仁 共回答了13个问题 |采纳率92.3%解题思路:(1)设点A、B的坐标分别为(x1,y1),(x2,y2),利用导数可求得过点A的切线方程为
+x1x 4
=1,由点P在切线上可得y1y 3
+x1 4
=1,同理,2y1 3
+x2 4
=1,由此可得AB方程;2y2 3
(2)设点P的坐标为(m,n),由(1)知,
+mx1 4
=1,问题转化为向量的夹角相等,利用向量夹角公式可得结论;ny1 3 (1)设点A的坐标为(x1,y1),
当y≥0时,由
x2
4+
y2
3=1得,y=
3(1−
x2
4),
则过点A的切线斜率k=y′|x=x1=
−
3
2x1
2
3(1−
x12
4)=−
3x1
4y1,过点A的切线方程为:y-y1=
−3x1
4y1(x−x1),
又
x12
4+
y12
3=1,则切线方程可整理为:
x1x
4+
y1y
3=1,
当y<0时,同理可得切线方程为:
x1x
4+
y1y
3=1,
综上,过点A的切线方程为:
x1x
4+
y1y
3点评:
本题考点: 直线与圆锥曲线的关系;椭圆的标准方程.
考点点评: 本题考查椭圆标准方程的求解、直线与椭圆的位置关系,考查学生分析问题解决问题的能力.1年前查看全部
- 直线l过点M(1,1),与椭圆x24+y23=1相交于A、B两点,若AB的中点为M,试求:
直线l过点M(1,1),与椭圆
+x2 4
=1相交于A、B两点,若AB的中点为M,试求:y2 3
(1)直线l的方程.
(2)求弦长AB. haifeiyuansui1年前1
haifeiyuansui1年前1 -
 我把你当做知音 共回答了15个问题
我把你当做知音 共回答了15个问题 |采纳率93.3%解题思路:(1)由于A,B两点是直线与椭圆的交点,故他们应满足椭圆方程,设出它们的坐标,然后根据它们的中点为M,可将坐标间的关系转化为求直线l的斜率,然后再由点斜式求出直线方程;
(2)3x+4y-7=0与椭圆
+x2 4
=1联立,利用韦达定理,结合弦长公式,可求弦长AB.y2 3 (1)设A(x1,y1)、B(x2,y2),
则
x12
4+
y12
3=1,①
x22
4+
y22
3=1②
①-②,得
(x1-x2)(x1+x2)
4+
(y1-y2)(y1+y2)
3=0.
又∵M为AB中点,
∴x1+x2=2,y1+y2=2.
∴直线l的斜率为-[3/4].
∴直线l的方程为y-1=-[3/4](x-1),即3x+4y-7=0.
(2)3x+4y-7=0与椭圆
x2
4+
y2
3=1联立可得21x2-42x+1=0,
设A(x1,y1),B(x2,y2),则x1+x2=2,x1x2=[1/21],
∴|AB|=
1+
9
16•
4-
4
21=
5
21
105.点评:
本题考点: 椭圆的简单性质.
考点点评: 本题考查直线与椭圆的综合,考查弦中点问题,正确运用点差法解决中点弦问题是解题的关键,属于中档题.1年前查看全部
- 椭圆x24+y23=1的左焦点为F,直线x=m与椭圆相交于点A、B,当△FAB的周长最大时,△FAB的面积是( )
椭圆
+x2 4
=1的左焦点为F,直线x=m与椭圆相交于点A、B,当△FAB的周长最大时,△FAB的面积是( )y2 3
A.[1/2]
B.2
C.[1/3]
D.3 yvenavbww1年前0
yvenavbww1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 椭圆x24+y23=1的左焦点为F,直线x=m与椭圆相交于点A、B,当△FAB的周长最大时,△FAB的面积是( )
椭圆
+x2 4
=1的左焦点为F,直线x=m与椭圆相交于点A、B,当△FAB的周长最大时,△FAB的面积是( )y2 3
A. [1/2]
B. 2
C. [1/3]
D. 3 wangkexin1年前0
wangkexin1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 过椭圆x24+y23=1的右焦点F2的直线交椭圆于于M,N两点,令|F2M|=m,|F2N|=n,则[mn/m+n]=[
过椭圆
+x2 4
=1的右焦点F2的直线交椭圆于于M,N两点,令|F2M|=m,|F2N|=n,则[mn/m+n]=y2 3 [3/4][3/4]. beauva1年前1
beauva1年前1 -
 fsakp532 共回答了19个问题
fsakp532 共回答了19个问题 |采纳率84.2%解题思路:设M(x1,y1),N(x2,y2),若过F2的直线存在斜率,设为k,所以这条直线的方程为y=k(x-1),联立椭圆的方程可以消去y,得到关于x的方程,根据韦达定理即可求出x1+x2,x1x2.根据椭圆上的点到右焦点的距离和它到右准线的距离的比为离心率e,即可用x1,x2表示m,n,带入[mn/m+n]中用上韦达定理得出的x1+x2,x1x2即可求出[mn/m+n].若这条直线不存在斜率,可求得方程为x=1,带入椭圆方程即可求得y值,从而得到M,N两点的坐标,从而可以求出m,n带入[mn/m+n]即可.若过F2的直线存在斜率时,设斜率为k,M(x1,y1),N(x2,y2),则该直线的方程为y=k(x-1),
联立椭圆方程:
x2
4+
y2
3=1得:(3+4k2)x2-8k2x+4k2-12=0;
x1+x2=
8k2
3+4k2,x1x2=
4k2−12
3+4k2;
该椭圆的右准线方程为:x=4,e=[1/2],点M,N到准线的距离分别为:4-x1,4-x2;
∴根据椭圆上的点到右焦点的距离与它到右准线的距离的比为e:[1/2],可以得到:
m=[1/2](4-x1),n=[1/2](4-x2);
∴[mn/m+n=
1
4(4−x1)(4−x2)
1
2[8−(x1+x2)]=
x1x2−4(x1+x2)+16
16−2(x1+x2)]=
4k2−12
3+4k2−
32k2
3+4k2+16
16−
16k2
3+4k2=
36k2+36
48k2+48=
3
4;
若过F2的直线不存在斜率时,该直线方程为:x=1,带入椭圆方程得到y=±
3
2,不妨设M(1,点评:
本题考点: 椭圆的简单性质.
考点点评: 考查椭圆的标准方程,焦点,准线,离心率,直线的方程以及韦达定理.1年前查看全部
- 椭圆x24+y23=1的左焦点为F,直线x=m与椭圆相交于点A、B,当△FAB的周长最大时,△FAB的面积是______
椭圆
+x2 4
=1的左焦点为F,直线x=m与椭圆相交于点A、B,当△FAB的周长最大时,△FAB的面积是______.y2 3  danfulw1年前0
danfulw1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- (2013•湛江一模)椭圆x24+y23=1的左、右焦点分别为F1、F2,P是椭圆上任一点,则|PF1|•|PF2|的取
(2013•湛江一模)椭圆
+x2 4
=1的左、右焦点分别为F1、F2,P是椭圆上任一点,则y2 3
•|PF1|
的取值范围是( )|PF2|
A.(0,4]
B.(0,3]
C.[3,4)
D.[3,4] nieyeling1年前1
nieyeling1年前1 -
 我p不淘你们家 共回答了15个问题
我p不淘你们家 共回答了15个问题 |采纳率93.3%解题思路:根据椭圆方程设出P的坐标,求出F1、F2,坐标,然后表示出
•|PF1|
.利用三角函数的有界性求出数量积的范围.|PF2| 因为椭圆
x2
4+
y2
3=1的左、右焦点分别为F1(-1,0),F2(1,0),
P是椭圆上任一点(2cosθ,
3sinθ),θ∈R
所以
PF1=(−1−2cosθ,−
3sinθ),
PF2=(1−2cosθ,−
3sinθ),
所以
|PF1|•
|PF2|=
(−1−2cosθ)2+3sin2θ•
(1−2cosθ)2+3sin2θ
=
(2+cosθ)2•
(2−cosθ)2
=4-cos2θ
因为θ∈R,cos2θ∈[0,1],
4-cos2θ∈[3,4].
所以
|PF1|•
|PF2|的取值范围是:[3,4].
故选D.点评:
本题考点: 椭圆的参数方程;平面向量数量积的运算;椭圆的简单性质.
考点点评: 本题考查椭圆的简单性质,椭圆的参数方程,向量的数量积的应用,三角函数的值域,考查计算能力.1年前查看全部
- (2008•海珠区一模)已知抛物线D的顶点是椭圆x24+y23=1的中心,焦点与该椭圆的右焦点重合.
(2008•海珠区一模)已知抛物线D的顶点是椭圆
+x2 4
=1的中心,焦点与该椭圆的右焦点重合.y2 3
(1)求抛物线D的方程;
(2)已知动直线l过点P(4,0),交抛物线D于A、B两点,坐标原点O为PQ中点,求证:∠AQP=∠BQP;
(3)是否存在垂直于x轴的直线m被以AP为直径的圆所截得的弦长恒为定值?如果存在,求出m的方程;如果不存在,说明理由. 萨飒1年前1
萨飒1年前1 -
 jara118717 共回答了20个问题
jara118717 共回答了20个问题 |采纳率100%解题思路:(1)由题意,设抛物线方程为y2=2px(p>0).由a2-b2=4-3=1,得c=1.由此能求出抛物线D的方程.
(2)设A(x1,y1),B(x2,y2),由于O为PQ之中点,故当l⊥x轴时由抛物线的对称性知∠AQP=∠BQP,当l不垂直x轴时,设l:y=k(x-4),由
,得k2x2-4(2k2+1)x+16k2=0,由此能够证明∠AQP=∠BQp.y=k(x−4) y2=4x
(3)设存在直线m+x=a满足题意,则圆心M(
,x1+4 2
),过M作直线x=a的垂线,垂足为E,故|EG|2=|MG|2-|ME|2,由此能够导出存在直线m:x=3满足题意.y1 2 (本小题满分14分)
(1)由题意,可设抛物线方程为y2=2px(p>0).
由a2-b2=4-3=1,得c=1.
∴抛物线的焦点为(1,0),∴p=2.
∴抛物线D的方程为y2=4x.…(4分)
(2)证明:设A(x1,y1),B(x2,y2),
由于O为PQ之中点,故当l⊥x轴时,由抛物线的对称性知,一定有∠AQP=∠BQP,
当l不垂直x轴时,设l:y=k(x-4),
由
y=k(x−4)
y2=4x,得k2x2-4(2k2+1)x+16k2=0,
∴
x1+x2=
4(2k2+1)
k2
x1x2=16,
∵kAQ=
y1
x1+4=
k(x1−4)
x1+4,
kBQ=
y2
x2+4=
k(x2−4)
x2+4,
∴kAQ+kBQ=
k(2x1x2−32)
(x1+4)(x点评:
本题考点: 直线与圆锥曲线的综合问题;圆锥曲线的综合.
考点点评: 本题考查抛物线方程的求法,直线和抛物线的位置关系,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.1年前查看全部
- 在直角坐标系xOy中 已知椭圆C:x24+y23=1上一点P(1,[3/2]),过点P的直线l1,l2与椭圆C分别交于点
在直角坐标系xOy中 已知椭圆C:
+x2 4
=1上一点P(1,[3/2]),过点P的直线l1,l2与椭圆C分别交于点A、B,且他们的斜率k1,k2满足k1.k2=-[3/4],求证:y2 3
(1)直线AB过定点;
(2)求△PAB面积的最大值. mukemei251年前0
mukemei251年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 椭圆x24+y23=1的上,下顶点分别为A1,A2,左顶点为B1,左焦点为F1,若直线A1F1交直线A2B1于点D,则c
椭圆
+x2 4
=1的上,下顶点分别为A1,A2,左顶点为B1,左焦点为F1,若直线A1F1交直线A2B1于点D,则cos∠B1DF1=y2 3 7 14 .7 14  teachyou251年前0
teachyou251年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 已知直线过椭圆x24+y23=1的左焦点F1,且与椭圆交于A,B两点,过点A,B分别作椭圆的两条切线,则其交点的轨迹方程
已知直线过椭圆
+x2 4
=1的左焦点F1,且与椭圆交于A,B两点,过点A,B分别作椭圆的两条切线,则其交点的轨迹方程______.y2 3  看星的人1年前1
看星的人1年前1 -
 zhouchang1 共回答了12个问题
zhouchang1 共回答了12个问题 |采纳率83.3%解题思路:分别求出椭圆在点A、B处的切线方程,联立方程组能求出交点的轨迹方程.当直线l的斜率存在时,设为k,直线l的方程为y=k(x+1),
设A(x1,y1),B(x2,y2),
则椭圆在点A处的切线方程为:
x1x
4+
y1y
3=1,①
椭圆在点B的切线方程为:
x2x
4+
y2y
3=1,②
联立方程①②得:x=
4(y2−y1)
x1y2−x2y1=
4k(x2−x1)
x1k(x2−1)−x2k(x1+1)=-4,
即此时交点的轨迹方程:x=-4.
当直线l的斜率不存在时,直线l的方程为x=-1,
此时A(-1,1.5),B(-1,-1.5),经过AB两点的切线交点为(-4,0).
综上所述,切线的交点的轨迹方程为:x=-4.
故答案为:x=-4.点评:
本题考点: 椭圆的简单性质.
考点点评: 本题考查切线方程的求法,考查椭圆方程的求法,考查交点的轨迹方程的求法,解题时要认真审题,注意计算能力、推理论证能力的培养.1年前查看全部
- 若直线mx+ny=4和⊙O:x2+y2=4相交,则点P(m,n)与椭圆C:x24+y23=1的位置关系为( )A.点P
若直线mx+ny=4和⊙O:x2+y2=4相交,则点P(m,n)与椭圆C:x24+y23=1的位置关系为( )A.点P在椭圆C
若直线mx+ny=4和⊙O:x2+y2=4相交,则点P(m,n)与椭圆C:
+x2 4
=1的位置关系为( )y2 3
A.点P在椭圆C内
B.点P在椭圆C上
C.点P在椭圆C外
D.以上三种均有可能
 qingliao1年前1
qingliao1年前1 -
 苦焚 共回答了17个问题
苦焚 共回答了17个问题 |采纳率82.4%∵直线mx+ny=4和⊙O:x2+y2=4相交,∴圆心(0,0)到直线的距离d<r.
∴
4
m2+n2<2,化为m2+n2>4.
∴m2>4-n2.
∵
m2
4+
n2
3>
4?n2
4+
n2
3=1+
n2
12>1,
∴点P(m,n)在椭圆C:
x2
4+
y2
3=1的外部.
故选:C.1年前查看全部
- 设椭圆x24+y23=1的长轴两端点为M、N,点P在椭圆上,则PM与PN的斜率之积为( )
设椭圆
+x2 4
=1的长轴两端点为M、N,点P在椭圆上,则PM与PN的斜率之积为( )y2 3
A.−3 4
B.−4 3
C.[3/4]
D.[4/3] lipengking1年前0
lipengking1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- F1、F2为椭圆x24+y23=1的左、右焦点,A为椭圆上任一点,过焦点F1向∠F1AF2的外角平分线作垂线,垂足为D,
F1、F2为椭圆
+x2 4
=1的左、右焦点,A为椭圆上任一点,过焦点F1向∠F1AF2的外角平分线作垂线,垂足为D,则点D的轨迹方程是 ___ .y2 3
 zhidafeng1年前0
zhidafeng1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- (2014•包头二模)设F1,F2分别是椭圆E:x24+y23=1的左,右焦点,过F1的直线l与E相交于A,B两点,且|
(2014•包头二模)设F1,F2分别是椭圆E:
+x2 4
=1的左,右焦点,过F1的直线l与E相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列,则|AB|=( )y2 3
A.[10/3]
B.3
C.[8/3]
D.2 创意人生路1年前1
创意人生路1年前1 -
 斜阳孤鸿 共回答了20个问题
斜阳孤鸿 共回答了20个问题 |采纳率95%解题思路:首先,根据椭圆的定义,得到|AF1|+|AF2|=2a,|BF1|+|BF2|=2a,然后,两式相加,然后再结合条件|AF2|,|AB|,|BF2|成等差数列,建立等式,求解|AB|的长.∵椭圆E:
x2
4+
y2
3=1,
∴2a=4,
∴|AF1|+|AF2|=2a,|BF1|+|BF2|=2a,
∴|AF1|+|AF2|+|BF1|+|BF2|=4a,
∴|AB|+|BF2|+|AF2|=4a,
∵|AF2|,|AB|,|BF2|成等差数列,
∴2|AB|=|BF2|+|BF2|,
∴3|AB|=4a=8,
∴3|AB|=8,
∴|AB|=[8/3],
故选:C.点评:
本题考点: 椭圆的简单性质.
考点点评: 本题重点考查了椭圆的概念,属于基础题.对于利用椭圆的概念求解问题时,一定要认真审题,直线必过焦点时,才能用椭圆的定义.1年前查看全部
- 已知椭圆x24+y23=1的长轴的左、右端点分别为A、B,在椭圆上有一个异于点A、B的动点P,若直线PA的斜率kPA=[
已知椭圆
+x2 4
=1的长轴的左、右端点分别为A、B,在椭圆上有一个异于点A、B的动点P,若直线PA的斜率kPA=[1/2],则直线PB的斜率kPB为( )y2 3
A. [3/4]
B. [3/2]
C. -[3/4]
D. -[3/2] 4587451年前2
4587451年前2 -
 miuCat 共回答了14个问题
miuCat 共回答了14个问题 |采纳率85.7%解题思路:设P(m,n),则
+m2 4
=1.即有n2=[3/4](4-m2),由椭圆方程可得左右顶点A,B,再利用斜率的计算公式化简整理代入即可得到PA,PB的斜率之积,再由PA的斜率,即可得到PB的斜率.n2 3 由椭圆
x2
4+
y2
3=1 得a2=4,解得a=2,
即有A(-2,0),B(2,0),
设P(m,n),则
m2
4+
n2
3=1.
即有n2=[3/4](4-m2),
则kPA=[n/m+2],kPB=[n/m-2],
即有kPA•kPB=[n/m+2]•[n/m-2]
=
n2
m2-4=[3/4]•
4-m2
m2-4=-[3/4].
由于直线PA的斜率kPA=[1/2],
则直线PB的斜率kPB为-[3/4]×2=-[3/2],
故选D.点评:
本题考点: 椭圆的简单性质.
考点点评: 本题主要考查椭圆的几何性质,考查斜率公式的运用,以及化简整理和代入的能力,属于中档题.1年前查看全部
- (2012•四川)椭圆x24+y23=1的左焦点为F,直线x=m与椭圆相交于点A、B,当△FAB的周长最大时,△FAB的
(2012•四川)椭圆
+x2 4
=1的左焦点为F,直线x=m与椭圆相交于点A、B,当△FAB的周长最大时,△FAB的面积是______.y2 3  秋天中的树苗1年前0
秋天中的树苗1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 已知抛物线D的顶点是椭圆x24+y23=1的中心,焦点与该椭圆的右焦点重合
已知抛物线D的顶点是椭圆
+x2 4
=1的中心,焦点与该椭圆的右焦点重合y2 3
(1)求抛物线D的方程;
(2)已知动直线l过点P(4,0),交抛物D于A,B两点,坐标原点O为PQPQ中点,求证∠AQP=∠BQP. 问题女友1年前1
问题女友1年前1 -
 理想太远 共回答了21个问题
理想太远 共回答了21个问题 |采纳率95.2%解题思路:(1)由题意,设抛物线方程为y2=2px(p>0).由a2-b2=4-3=1,得c=1.由此能求出抛物线D的方程.(2)设A(x1,y1),B(x2,y2),由于O为PQ之中点,故当l⊥x轴时由抛物线的对称性知∠AQP=∠BQP,当l不垂直x轴时,设l:y=k(x-4),代入抛物线方程,得k2x2-4(2k2+1)x+16k2=0,由此能够证明∠AQP=∠BQP.(1)由题意,可设抛物线方程为y2=2px(p>0).
由a2-b2=4-3=1,得c=1.
∴抛物线的焦点为(1,0),∴p=2.
∴抛物线D的方程为y2=4x.…
(2)证明:设A(x1,y1),B(x2,y2),
由于O为PQ之中点,故当l⊥x轴时,由抛物线的对称性知,一定有∠AQP=∠BQP,
当l不垂直x轴时,设l:y=k(x-4),
代入抛物线方程,得k2x2-4(2k2+1)x+16k2=0,
∴x1+x2=
4(2k2+1)
k2,x1x2=16,
∵kAQ=
y1
x1+4,kBQ=
y2
x2+4,
∴kAQ+kBQ=
k(2x1x2−32)
(x1+4)(x2+4)=0,
∴∠AQP=∠BQP.
综上证知,∠AQP=∠BQP.点评:
本题考点: 直线与圆锥曲线的关系;抛物线的标准方程.
考点点评: 本题考查抛物线方程的求法,直线和抛物线的位置关系,考查运算求解能力,推理论证能力;考查化归与转化思想.1年前查看全部
- 已知椭圆x24+y23=1的长轴为线段AB,点M是椭圆上不同于A,B的任意一点,
已知椭圆
+x2 4
=1的长轴为线段AB,点M是椭圆上不同于A,B的任意一点,y2 3
(1)设直线MA,MB的斜率分别为k1,k2,求证:k1k2为定值;
(2)若直线MA,MB与直线x=3分别相交于C,D两点,求证:以CD为直径的圆过定点,并求出定点的坐标. 于添添1年前1
于添添1年前1 -
 山佳猪猪 共回答了17个问题
山佳猪猪 共回答了17个问题 |采纳率88.2%解题思路:(1)设M(x0,y0),则x024+y023=1,由已知得A(-2,0),B(2,0),由此能证明k1k2=y0x0+2•y0x0−2=y02x02−4=-34,为定值.(2)设直线MA:y1=k1(x+2),直线MB:y2=k2(x-2),由已知得C(3,5k1),D(3,k2),以CD为直径的圆方程为(x-3)2+[y-12(5k1+k2)]2=14(5k1-k2)2,化简得 x2-6x+9+y2-(5k1+k2)y=-5k1k2=154,由此能证明以CD为直径的圆过定点(3+152,0)和(3-152,0).证明:(1)设M(x0,y0),则
x02
4+
y02
3=1,
∴
y02
3=1-
x02
4=
4−x02
4,
∴
y02
x02−4=-[3/4],
∵椭圆
x2
4+
y2
3=1的长轴为线段AB,
∴A(-2,0),B(2,0),
∴k1=
y0
x0+2,k2=
y0
x0−2,
∴k1k2=
y0
x0+2•
y0
x0−2=
y02
x02−4=-[3/4],
∴k1k2为定值-[3/4].
(2)设直线MA:y1=k1(x+2),直线MB:y2=k2(x-2),
∵直线MA,MB与直线x=3分别相交于C,D两点,
∴C(3,5k1),D(3,k2)
∴以CD为直径的圆方程为(x-3)2+[y-[1/2](5k1+k2)]2=[1/4](5k1-k2)2,
化简得 x2-6x+9+y2-(5k1+k2)y=-5k1k2=[15/4],
∴以CD为直径的圆过定点(3+
15
2,0)和(3-
15
2,0).点评:
本题考点: 直线与圆锥曲线的综合问题.
考点点评: 本题考查两直线的斜率的乘积这定值的证明,考查圆过定点的证明,解题时要认真审题,注意椭圆性质的合理运用.1年前查看全部
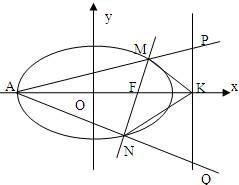
- (2010•武昌区模拟)如图,已知椭圆x24+y23=1的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线l交
 (2010•武昌区模拟)如图,已知椭圆
(2010•武昌区模拟)如图,已知椭圆
+x2 4
=1的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线l交x轴于点K,左顶点为A.y2 3
(1)求证:KF平分∠MKN;
(2)直线AM、AN分别交准线l于点P、Q,设直线MN的倾斜角为θ,试用θ表示线段PQ的长度|PQ|,并求|PQ|的最小值. 仙姑7805281年前1
仙姑7805281年前1 -
 z53575430 共回答了12个问题
z53575430 共回答了12个问题 |采纳率83.3%解题思路:(1)法一:几何法,分别过M和N点作准线的垂线,并设出对应的垂足,根据直角梯形列出比例关系,再由椭圆的第二定义,将到焦点的距离之比转化到对应准线的距离之比,判断出∠KMM1=∠KNN1,再由内错角相等得到∠MKF=∠NKF,即得到证明;
法二:代数法,根据题意设直线MN的方程为x=my+1,再设出点M、N的坐标,联立直线和椭圆的方程,消去x得到关于y的一个二次方程,根据韦达定理表示出y1+y2和y1y2,再代入斜率公式,进行证明;
(2)由题意求出点A和右准线的方程,并设出四点M、N、P和Q的坐标,根据A,M,P三点共线得到对应的斜率相等,求出点P和Q的坐标,联立直线和椭圆的方程,消去x得到关于y的一个二次方程,根据韦达定理表示出y1+y2和y1y2,再代入两点之间的距离公式,化简后用m表示|PQ|,再把m用cotθ表示,利用三角恒等变换公式和θ∈(0,π),求出最小值.(1)法一:作MM1⊥l于M1,
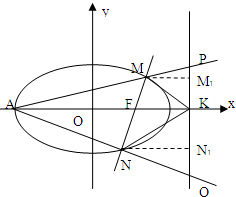
NN1⊥l于N1,则
|MF|
|NF|=
|M1K|
|N1K|,
由椭圆的第二定义,有
|MF|
|NF|=
|M1M|
|N1N|,
∴
|N1K|
|NN1|=
|M1K|
|MM1|,
∴∠KMM1=∠KNN1,即∠MKF=∠NKF,
∴KF平分∠MKN.
法二:设直线MN的方程为x=my+1,
设M、N的坐标分别为(x1,y1),(x2,y2),
由
x=my+1
x2
4+
y2
3=1得,(3m2+4)y2+6my-9=0,
∴y1+y2=-
6m
3m2+4,y1y2=-
9
3m2+4
设KM和KN的斜率分别为k1,k2,显然只需证k1+k2=0即可.
∵K(4,0),∴k1+k2=
y1
x1-4+
y2
x2-4=
x2y1+x1y2-4(y1+y2)
(x1-4)(x2-4)
而x2y1+x1y2-4(y1+y2点评:
本题考点: 直线与圆锥曲线的综合问题.
考点点评: 本题主要考查了直线与椭圆的综合问题,两点间的距离公式等基础知识,考查用代数方法研究圆锥曲线的性质和数形结合的数学思想,考查了学生解决问题的能力和运算能力.1年前查看全部
- 已知A,B为椭圆x24+y23=1的左右两个顶点,F为椭圆的右焦点,P为椭圆上异于A、B点的任意一点,直线AP、BP分别
已知A,B为椭圆
+x2 4
=1的左右两个顶点,F为椭圆的右焦点,P为椭圆上异于A、B点的任意一点,直线AP、BP分别交椭圆的右准线于M、N点,则△MFN面积的最小值是( )y2 3
A.8
B.9
C.11
D.12 猫猫还好吗1年前1
猫猫还好吗1年前1 -
 vip0005 共回答了14个问题
vip0005 共回答了14个问题 |采纳率85.7%解题思路:先设P(s,t),由题设条件得两直线PA,PB的方程,与准线方程联立,解出M,N两点的坐标,用s,t表示出线段MN的长度,再由点P在椭圆上,将点的坐标代入椭圆方程,用s表示出t,消去t,得到线段MN的长关于s的函数,又点F到准线的距离是3,由此MFN面积可表示为s的函数,由其形式知,可用判别式法求最小值设P(s,t),由题意直线PA的方程为[y/t+
x−2
s+2=1,即,直线PB的方程为
y
t+
x+2
s−2=1
由于椭圆
x2
4+
y2
3=1故a=2,b=
3],c=1,故其右准线方程为x=
a2
c=4,F(1,0),故F到准线的距离是3
∵直线AP、BP分别交椭圆的右准线于M、N点
∴M(4,[6/s+2t),N(4,
2
s−2t)
故有|MN|=|
6
s+2t-
2
s−2t|=|
4t(s−4)
s2−4]|
∴S2=[1/4]×|MN|2×9=[9/4]×|
4t(s−4)
s2−4|①
又P(s,t)在椭圆上,故有t2=3−
s2
4 代入①整理得S2=27×
(4−s)2
4−s2
令M2=
(4−s)2
4−s2得(M2+1)s2-8s+16-4M2=0,此方程恒有根
故△=64-4(M2+1)(16-4M2)≥0
解得M2≥3,故M≥
3或M≤-
3(舍)
∴S2=27×
(4−s)2
4−s2≥27×3
∴S≥9
故选B.点评:
本题考点: 椭圆的应用;椭圆的简单性质.
考点点评: 本题主要考查了椭圆的标准方程和直线与椭圆的关系,考查了学生综合分析问题和解决问题的能力.解题的关键是根据意建立起面积关于坐标的函数,掌握用判别式法求值域也是本题的一个难点,解题时运算技巧很重要.本题运算量很大,要严谨,避免因运算失误导致解题失败.1年前查看全部
大家在问
- 1堰塞湖形成的人为原因?
- 2今有A、B、C、D、E五种装置如图示.
- 3数学分式问题1、已知分式-6a+18/a²-9的值为正整数,求整数a的值2、已知|a-2|+(b+1)
- 4为什么移动电话用微波来通信?为什么不用长波,中波...
- 5水平弹簧振子的振动周期为0.4s 振幅为5cm
- 6(m的平方减4)乘以x的平方-(m-2)乘以x加8=0是关于x的一元一次方程,m是多少?
- 7大豆中有矿物质吗?
- 8呵护为题的作文600
- 9how do they sometimes keep in touch with each other?是什么意思?
- 10英语翻译Dear all,FYIIf you find wrong,please let me know,thanks!
- 11下列物质混合后,不能发生复分解反应的一组是( ) A.K 2 SO 4 溶液和Ba(OH) 2 溶液混合 B.KCl溶
- 12书面表达(满分25分)假设你是李华。美国一所友好学校准备与你们学校共同创办一份中学生英文刊物,该校格林先生来信询问有关情
- 13I saw Helen at the party last month. It _________ a year sin
- 14“请原谅信中可能会出现的语法错误”怎么翻?很高兴认识你 怎么翻?
- 15问个关于be动词的问题当句中(名词)and(名词)is/are.第一个名词是复数,第二个是单数因该用is还是are?
