f(x)=ax2+bx+1(a,b属于R),求(1)若f(-1)=0,且对任意实数x均有f(x)大于等于0成立,求a、b
 上弦1232022-10-04 11:39:541条回答
上弦1232022-10-04 11:39:541条回答(2)在(1)的条件下,当x属于【-2,2】时,g(x)=f(x)-Kx是单调函数,求K的取值范围
希望能说得详细点

已提交,审核后显示!提交回复
共1条回复
 青山绿水163 共回答了15个问题
青山绿水163 共回答了15个问题 |采纳率100%- 若f(-1)=0,且对任意实数x均有f(x)大于等于0成立,求a、b的值
所以可知有:
a-b+c=0,则b=a+1
△=b^2-4a0
则代入得
a^2+1-2a - 1年前
相关推荐
- 已知函数f(x)=ax2+bx+1(a,b为实数),x∈R,F(x)=f(x)(x>0)−f(x)(x<0)
已知函数f(x)=ax2+bx+1(a,b为实数),x∈R,F(x)=
f(x)(x>0) −f(x)(x<0)
(1)若f(-1)=0,且函数f(x)的值域为[0,+∞),求F(x)的表达式;
(2)在(1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围. 等待雕琢1年前1
等待雕琢1年前1 -
 lijllijl 共回答了23个问题
lijllijl 共回答了23个问题 |采纳率87%解题思路:(1)利用f(-1)=0和函数f(x)的值域为[0,+∞),建立方程关系,即可求出a,b,从而确定F(x)的表达式;
(2)在(1)的条件下,当x∈[-2,2]时,利用g(x)=f(x)-kx的单调区间与对称轴之间的关系建立不等式进行求解即可.(1)∵f(-1)=0,
∴a-b+1=0,①
∵函数f(x)的值域为[0,+∞),
∴a>0且判别式△=0,即b2-4a=0,②
由①②得a=1,b=2.
∴f(x)=ax2+bx+1═x2+2x+1.
∴F(x)=
x2+2x+1,x>0
−x2−2x−1, x<0.
(2)g(x)=f(x)-kx=x2+(2-k)x+1,
函数的对称轴为x=−
2−k
2=
k−2
2,
要使函数g(x)=f(x)-kx,在x∈[-2,2]上是单调函数,
则区间[-2,2]必在对称轴的一侧,
即
k−2
2≥2或
k−2
2≤−2,
解得k≥6或k≤-2.
即实数k的取值范围是k≥6或k≤-2.点评:
本题考点: 函数单调性的性质;函数解析式的求解及常用方法.
考点点评: 本题主要考查二次函数的图象和性质,以及二次函数单调性与对称轴之间的关系.1年前查看全部
- 已知函数f(x)=ax2+bx+1(a,b为实数),x属于R.x大于0时F(x)=f(x);x小于0时,F(x)=-f(
已知函数f(x)=ax2+bx+1(a,b为实数),x属于R.x大于0时F(x)=f(x);x小于0时,F(x)=-f(x),设mn0,a>0,且函数f(x)为偶函数,判断F(m)+F(n)是否大于0
 eedoxin1年前3
eedoxin1年前3 -
 永远的天空 共回答了18个问题
永远的天空 共回答了18个问题 |采纳率100%f(x)为偶函数,则f(x)=f(-x),得b=0
f(x)=ax^2+1,在[0,+无穷大)递增
如果m>0,则n-n,F(m)+F(n)=f(m)-f(n)=f(m)-f(-n)>0
同理,如果m0,n>-m,F(m)+F(n)=-f(m)+f(n)=f(n)-f(-m)>01年前查看全部
- 已知ax2+bx+1与2x2-3x+1的积不含x3的项,也不含x的项,求(a-b)2的值.
 尺码大1年前1
尺码大1年前1 -
 wgs2005wgs 共回答了16个问题
wgs2005wgs 共回答了16个问题 |采纳率93.8%解题思路:首先利用多项式乘法法则计算出(ax2+bx+1)(2x2-3x+1),再根据积不含x3的项,也不含x的项,可得含x3的项和含x的项的系数等于零,进而算出a、b的值.再计算(a-b)2的值即可.(ax2+bx+1)(2x2-3x+1),
=ax4-3ax3+ax2+2bx3-3bx2+bx+2x2-3x+1,
∵积不含x3的项,也不含x的项,
∴-3a+2b=0,b-3=0,
解得:b=3,a=2,
则(a-b)2=(2-3)2=1.点评:
本题考点: 多项式乘多项式.
考点点评: 此题主要考查了多项式乘以多项式,关键是掌握多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加.1年前查看全部
- 已知函数f(x)=ax2+bx+1(a,b为实数,a≠0,x∈R).
已知函数f(x)=ax2+bx+1(a,b为实数,a≠0,x∈R).
(Ⅰ)当函数f(x)的图象过点(-1,0),且方程f(x)=0有且只有一个根,求f(x)的表达式;
(Ⅱ)在(Ⅰ)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围;
(Ⅲ)若F(x)=
当mn<0,m+n>0,a>0,且函数f(x)为偶函数时,试判断F(m)+F(n)能否大于0?f(x)x>0 −f(x)x<0  拓展者1年前1
拓展者1年前1 -
 weiwei718 共回答了18个问题
weiwei718 共回答了18个问题 |采纳率94.4%解题思路:(Ⅰ)根据f(-1)=0,可得a-b+1=0,再根据方程f(x)=0有且只有一个根,利用根的判别式再列出一个a和b的关系式,联立方程组即可解得a和b的值.
(Ⅱ)首先求出g(x)的函数关系式,然后根据函数的单调性进行解答,即可求出k的取值范围.
(Ⅲ)由f(x)为偶函数,求出b=0,设m>0,则n<0,又知m+n>0,故可得m>-n>0,最后把m和n代入求出F(m)+F(n)>0.(Ⅰ)因为f(-1)=0,所以a-b+1=0.(1分)
因为方程f(x)=0有且只有一个根,所以△=b2-4a=0.
所以b2-4(b-1)=0.即b=2,a=1.(3分)
所以f(x)=(x+1)2.(4分)
(Ⅱ)因为g(x)=f(x)-kx=x2+2x+1-kx=x2-(k-2)x+1
=(x−
k−2
2)2+1−
(k−2)2
4.(6分)
所以当[k−2/2≥2或
k−2
2≤−2时,
即k≥6或k≤-2时,g(x)是单调函数.(9分)
(Ⅲ)f(x)为偶函数,所以b=0.所以f(x)=ax2+1.
所以F(x)=
ax2+1x>0
−ax2−1x<0.](10分)
因为mn<0,不妨设m>0,则n<0.
又因为m+n>0,所以m>-n>0.
所以|m|>|-n|.(12分)
此时F(m)+F(n)=f(m)-f(n)=am2+1-an2-1=a(m2-n2)>0.
所以F(m)+F(n)>0.(14分)点评:
本题考点: 函数解析式的求解及常用方法;函数单调性的性质;奇偶性与单调性的综合.
考点点评: 本题主要考查函数解析式的求法、函数单调性的性质和奇偶性与单调性综合运用的知识点,解答本题的关键是熟练掌握函数单调性的性质,利用奇偶性进行解题,此题难度不是很大.1年前查看全部
- 多项式2x2-3x+1与ax2+bx+1的积不含x3项和x的项,求a与b的值
 Gxkudou1年前1
Gxkudou1年前1 -
 深蓝动力 共回答了16个问题
深蓝动力 共回答了16个问题 |采纳率81.3%x^3前的系数(2x^2)*bx-3x*(ax^2)
x^3前的系数和2b-3a=0
x前的系数(-3x)*1+1*(bx)
x前的系数和-3+b=0
解得a=2 ,b=31年前查看全部
- 已知函数f(x)=ax2+bx+1(a,b为实数),x∈R,F(x)=f(x)(x>0)-f(x)(x<0).
已知函数f(x)=ax2+bx+1(a,b为实数),x∈R,F(x)=
f(x)(x>0) -f(x)(x<0).
(1)若f(-1)=0,且函数f(x)≥0的对任意x属于一切实数成立,求F(x)的表达式;
(2)在 (1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围.
 loverracy1年前1
loverracy1年前1 -
 白雪xue 共回答了16个问题
白雪xue 共回答了16个问题 |采纳率87.5%解题思路:(1)根据f(-1)=0,可得b与a关系,又对任意实数x均有f(x)≥0成立,根据二次函数的性质,即可得到关于a和b的不等关系,从而求得a和b的值,即可得F(x)的表达式;
(2)由(1)中可得f(x)的解析式,从而求得g(x)的解析式,根据二次函数的性质可知,当对称轴在区间两侧的时候,函数f(x)为单调函数,可以得到2≤[k−2/2]或[k−2/2]≤-2,求解即可求得实数k的取值范围.(1)由题意,函数f(x)=ax2+bx+1(a,b为实数),
∵f(-1)=0,
∴a-b+1=0,即b=a+1,
∵函数f(x)≥0对任意x属于一切实数恒成立,即ax2+bx+1≥0对x∈R恒成立,
∴
a>0
△=b2-4a≤0,
∵b=a+1,
∴
a>0
(a+1)2-4a=(a-1)2≤0,
∴a=1,b=2,
∴f(x)=x2+2x+1,
∴F(x)=
x2+2x+1(x>0)
-x2-2x-1(x<0);
(2)由(1)可知,f(x)=x2+2x+1,
∵g(x)=f(x)-kx,
∴g(x)=x2+(2-k)x+1=(x-
k-2
2)2+1-
(k-2)2
4,
∵对称轴为x=[k-2/2],函数g(x)的图象开口向上,
∴g(x)在(-∞,[k-2/2]]上是单调递减函数,在[[k-2/2],+∞)上是单调递增函数,
∵g(x)在x∈[-2,2]时是单调函数,
∴[-2,2]⊂(-∞,[k-2/2]]或[-2,2]⊂[[k-2/2],+∞),
∴2≤[k-2/2]或[k-2/2]≤-2,解得k≥6或k≤-2,
∴实数k的取值范围为(-∞,-2]∪[6,+∞).点评:
本题考点: 函数单调性的性质;分段函数的解析式求法及其图象的作法.
考点点评: 本题考查了函数单调性的性质,分段函数解析式的求法.本题重点考查了二次函数的性质,对于二次函数要注意数形结合的应用,注意抓住二次函数的开口方向,对称轴,以及判别式的考虑.属于中档题.1年前查看全部
- 给出三个命题:①点P(b,a)在抛物线y=x2+1上;②点A(1,3)能在抛物线y=ax2+bx+1上;③点B(-2,1
给出三个命题:①点P(b,a)在抛物线y=x2+1上;②点A(1,3)能在抛物线y=ax2+bx+1上;③点B(-2,1)能在抛物线y=ax2-bx+1上.若①为真命题,则( )
A. ②③都是真命题
B. ②③都是假命题
C. ②是真命题,③是假命题
D. ②是假命题,③是真命题 Finback20081年前1
Finback20081年前1 -
 7829109 共回答了16个问题
7829109 共回答了16个问题 |采纳率87.5%解题思路:分析是否为真命题,需要分别分析各题设是否能推出结论.根据题意,得
把点P(b,a)代入抛物线y=x2+1,得a=b2+1.
②中,把点A(1,3)代入抛物线y=ax2+bx+1,得a+b+1=3.
把a=b2+1,代入得b2+b-1=0,
△=1+4=5>0,则方程有解.
故原命题为真命题.
③中,把点B(-2,1)代入抛物线y=ax2-bx+1,得a(-2)2-b×(-2)+1=1,即4a+2b=0.
把a=b2+1代入,得4b2+4+2b=0,
△=4-4×4×4=-60<0,则方程无解.
故原命题为假命题.
故选C.点评:
本题考点: 命题与定理.
考点点评: 解答此题的关键是要熟知真命题与假命题的概念:
真命题:判断正确的命题叫真命题;
假命题:判断错误的命题叫假命题;1年前查看全部
- 当x=1时,代数式ax2+bx+1的值为3,则(a+b-1)(1-a-b)的值为( )
当x=1时,代数式ax2+bx+1的值为3,则(a+b-1)(1-a-b)的值为( )
A. 1
B. -1
C. 2
D. -2 Jerry_Von1年前3
Jerry_Von1年前3 -
 ANLOUISDY 共回答了18个问题
ANLOUISDY 共回答了18个问题 |采纳率94.4%解题思路:由题意可得出:当x=1时,a+b+1=3,即可求得a+b=2,将a+b整体代入得出(a+b-1)(1-a-b)求解即可.由题意得:a+b+1=3,可得a+b=2
将a+b=2代入得1(1-2)=-1
故选B.点评:
本题考点: 代数式求值.
考点点评: 本题考查代数式的求值,关键在于求出a+b的值,利用整体思想求解.注意括号前是负号时符号的变化.1年前查看全部
- 函数f(x)=ax2+bx+1(a大于0)若f(—1)=0,并对x属于R恒有f(x)大于等于0,求f(x)的表达式
 syjasa1年前1
syjasa1年前1 -
 漂雨的黄昏 共回答了18个问题
漂雨的黄昏 共回答了18个问题 |采纳率83.3%函数f(x)=ax2+bx+1(a大于0)若f(—1)=0,并对x属于R恒有f(x)大于等于0,有
a-b+1=0 △=b*b-4a≤0
(a+1)^2-4a≤0 即(a-1)^2≤0 ∴a=1 b=2
∴f(x)=x^2+2x+11年前查看全部
- 函数f(x)=ax2+bx+1(a>0)(1)若f(-1)=0,并对x∈R恒有f(x)≥0,求f(x)的表达式;(2)在
函数f(x)=ax2+bx+1(a>0)(1)若f(-1)=0,并对x∈R恒有f(x)≥0,求f(x)的表达式;(2)在(1)的条件下,对x∈[-1,1],g(x)=f(x)-kx是单调函数,求k的范围.
 e7qpa6g1年前1
e7qpa6g1年前1 -
 345196190 共回答了14个问题
345196190 共回答了14个问题 |采纳率85.7%解题思路:(1)由 f(-1)=0得a-b+1=0,又因为对x∈R恒有f(x)≥0,△=b2-4a≤0,得(a+1)2-4a≤0,从而求出a,b的值.
(2)首先表示出g(x)=x2+(2-k)x+1,根据单调故应满足
≥1或k−2 2
≤−1,从而求出k的取值范围.k−2 2 (1)由 f(-1)=0得a-b+1=0又因为对x∈R恒有f(x)≥0,△=b2-4a≤0,得(a+1)2-4a≤0,(a-1)2≤0,
所以a=1b=2得f(x)=x2+2x+1
(2)g(x)=f(x)-kx=x2+(2-k)x+1是单调函数,则
k−2
2≥1或
k−2
2≤−1,所以得k≥4或k≤0点评:
本题考点: 二次函数的性质;函数单调性的性质.
考点点评: 本题考查了二次函数的性质,主要是单调性的应用,属于基础重点题型,应该熟练掌握.1年前查看全部
- 已知函数f(x)=ax2+bx+1(a,b为实数),x∈R,
已知函数f(x)=ax2+bx+1(a,b为实数),x∈R,
(1)若f(x)有一个零点为-1,且函数f(x)的值域为[0,+∞),求f(x)的解析式;
(2)在(1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围. 柳客丛1年前1
柳客丛1年前1 -
 whb28910 共回答了15个问题
whb28910 共回答了15个问题 |采纳率86.7%解题思路:(1)由f(-1)=0,可得a-b+1=0,又函数f(x)的值域为[0,+∞),可得二次函数的对称轴,从而可求出a,b的值;
(2)由(1)可知f(x)=x2+2x+1,可得g(x)=x2+(2-k)x+1,由g(x)在x∈[-2,2]时是单调函数,可得[−2,2]⊂(−∞,
]或[−2,2]⊂[k−2 2
,+∞),从而得出2≤k−2 2
或k−2 2
≤−2,解之即可得出k的取值范围.k−2 2 (1)由题意得:
a−b+1=0
−
b
2a=−1解得:
a=1
b=2
所以:f(x)=x2+2x+1…(6分)
(2)由(1)得g(x)=x2+(2-k)x+1当x∈[-2,2]时,g(x)是单调函数的充要条件是:
[−2,2]⊂(−∞,
k−2
2]或[−2,2]⊂[
k−2
2,+∞),
-[2−k/2]≥2或−
2−k
2≤−2
解得:k≥6或k≤-2…(12分)点评:
本题考点: 二次函数的性质.
考点点评: 本题考查了函数的恒成立问题及函数单调性的应用,难度一般,关键是掌握函数单调性的应用.1年前查看全部
- 在(ax2+bx+1)(2x2-3x-1)的计算结果中,不含x3项和x项,求a,b的值.
 cxysjj1年前2
cxysjj1年前2 -
 lirongyuyu 共回答了26个问题
lirongyuyu 共回答了26个问题 |采纳率88.5%解题思路:根据多项式乘以多项式法则展开,合并同类项,根据题意得出2b-3a=0,-3-b=0,求出即可.(ax2+bx+1)(2x2-3x-1)
=2ax4-3ax3-ax2+2bx3-3bx2-bx+2x2-3x-1
=2ax4+(2b-3a)x3+(-a-3b+2)x2+(-3-b)x-1,
∵在(ax2+bx+1)(2x2-3x-1)的计算结果中,不含x3项和x项,
∴2b-3a=0,-3-b=0,
解得:a=-2,b=-3.点评:
本题考点: 多项式乘多项式.
考点点评: 本题考查了多项式乘以多项式法则和二元一次方程组的应用,关键是能根据题意得出关于a、b的方程组.1年前查看全部
- 在(ax2+bx+1)(2x2-3x-1)的计算结果中,不含x3项和x项,求a,b的值.
 小野优子1年前1
小野优子1年前1 -
 chenshu01 共回答了18个问题
chenshu01 共回答了18个问题 |采纳率100%解题思路:根据多项式乘以多项式法则展开,合并同类项,根据题意得出2b-3a=0,-3-b=0,求出即可.(ax2+bx+1)(2x2-3x-1)
=2ax4-3ax3-ax2+2bx3-3bx2-bx+2x2-3x-1
=2ax4+(2b-3a)x3+(-a-3b+2)x2+(-3-b)x-1,
∵在(ax2+bx+1)(2x2-3x-1)的计算结果中,不含x3项和x项,
∴2b-3a=0,-3-b=0,
解得:a=-2,b=-3.点评:
本题考点: 多项式乘多项式.
考点点评: 本题考查了多项式乘以多项式法则和二元一次方程组的应用,关键是能根据题意得出关于a、b的方程组.1年前查看全部
- 已知函数f(x)=ax2+bx+1(a,b∈R且a≠0),F(x)=f(x),x>0−f(x),x<0.
已知函数f(x)=ax2+bx+1(a,b∈R且a≠0),F(x)=
.f(x),x>0 −f(x),x<0
(1)若f(-1)=0,且函数f(x)的值域为[0,+∞),求F(x)的解析式;
(2)在(1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围;
(3)设mn<0,m+n>0,a>0,且f(x)是偶函数,判断F(m)+F(n)是否大于零. 俊迷1年前1
俊迷1年前1 -
 wenhoujun8 共回答了16个问题
wenhoujun8 共回答了16个问题 |采纳率93.8%解题思路:(1)利用f(-1)=0和函数f(x)的值域为[0,+∞),建立方程关系,即可求出a,b,从而确定F(x)的表达式;
(2)在(1)的条件下,当x∈[-2,2]时,利用g(x)=f(x)-kx的单调区间与对称轴之间的关系建立不等式进行求解即可.
(3)利用mn<0,m+n>0,a>0,且f(x)是偶函数,得到b=0,然后判断F(m)+F(n)的取值.(1)∵f(-1)=0,
∴a-b+1=0,①
∵函数f(x)的值域为[0,+∞),
∴a>0且判别式△=0,即b2-4a=0,②
由①②得a=1,b=2.
∴f(x)=ax2+bx+1=x2+2x+1.
∴F(x)=
x2+2x+1,x>0
−x2−2x−1, x<0.
(2)g(x)=f(x)-kx=x2+(2-k)x+1,
函数的对称轴为x=−
2−k
2=
k−2
2,
要使函数g(x)=f(x)-kx,在x∈[-2,2]上是单调函数,
则区间[-2,2]必在对称轴的一侧,
即[k−2/2≥2或
k−2
2≤−2,
解得k≥6或k≤-2.
即实数k的取值范围是k≥6或k≤-2.
(3)∵f(x)是偶函数,∴f(-x)=f(x),
即ax2-bx+1=ax2+bx+1,
∴2bx=0,解得b=0.
∴f(x)=ax2+1.
∴F(x)=
ax2+1,x>0
−ax2−1,x<0].
∵mn<0,m+n>0,a>0,
不妨设m>n,则m>0,n<0,
∴F(m)+F(n)=am2+1-an2-1=a(m2-n2)=a(m-n)(m+n),
∵m+n>0,a>0,m-n>0,
∴F(m)+F(n)=a(m-n)(m+n)>0.点评:
本题考点: 函数单调性的判断与证明;函数解析式的求解及常用方法;函数奇偶性的判断.
考点点评: 本题主要考查二次函数的图象和性质,以及二次函数单调性与对称轴之间的关系.要求熟练掌握二次函数的相关知识.1年前查看全部
- 已知函数f(x)=ax2+bx+1(a,b为实数),x∈R,F(x)=f(x)(x>0)−f(x)(x<0)
已知函数f(x)=ax2+bx+1(a,b为实数),x∈R,F(x)=
f(x)(x>0) −f(x)(x<0)
(1)若f(-1)=0且函数f(x)的值域为[0,+∞),求F(x)的表达式;
(2)设mn<0,m+n>0,a>0,且f(x)为偶函数,判断F(m)+F(n)能否大于零?并说明理由. liubinghua81年前1
liubinghua81年前1 -
 artofzerg 共回答了17个问题
artofzerg 共回答了17个问题 |采纳率88.2%解题思路:(1)由f(-1)=0 可得a-b+1=0,由f(x)≥0恒成立,可得
,联立方程可求a,b,进而可求f(x),F(x)a>0 △=b2−4a=0
(2)由f(x)为偶函数,可得b=0,则有F(x)=
,不妨设m>0,n<0,从而可得|m|>|-n|,代入F(m)+F(n)=f(m)-f(n)=am2+1-(an2+1)=a(m2-n2)>0,即可ax2+1,x>0 −ax2−1,x <0 (1)∵f(-1)=0∴a-b+1=0
又x∈R,f(x)≥0恒成立,
∴
a>0
△=b2−4a=0
∴b2-4(b-1)=0∴a=1,b=2
∴f(x)=x2+2x+1
∴F(x)=
(x+1)2,x>0
−(x+1)2,x<0
(2)∵f(x)为偶函数,
∴f(x)=ax2+1
∴F(x)=
ax2+1,x>0
−ax2−1,x <0
∵mn<0设m>n,则m>0,n<0
又m+n>0
∴m>-n>0
∴|m|>|-n|,
∴F(m)+F(n)=f(m)-f(n)=am2+1-(an2+1)=a(m2-n2)>0
∴F(m)+F(n)能大于零.点评:
本题考点: 二次函数的性质;函数解析式的求解及常用方法.
考点点评: 本题主要考查了利用待定系数法求解二次函数的解析式,求解的关键是灵活利用二次函数的性质由f(x)≥0恒成立得a>0△=b2−4a=0.1年前查看全部
- 已知函数f(x)=ax2+bx+1(a,b为为实数),x∈R.
已知函数f(x)=ax2+bx+1(a,b为为实数),x∈R.
(1)若函数f(x)的最小值是f(-1)=0,求f(x)的解析式;
(2)在(1)的条件下,f(x)>x+k在区间[-3,-1]上恒成立,试求k的取值范围;
(3)若a>0,f(x)为偶函数,实数m,n满足mn<0,m+n>0,定义函数F(x)=
f(x),当x≥0-f(x),当x<0
,试判断F(m)+F(n)值的正负,并说明理由
(3)f(x)是偶函数,可得b=0,求得f(x)=ax2+1,由mn<0,m+n>0,可得m、n异号,设m>0,则n<0,故可得
m>-n>0,代入F(m)+F(n),化简成关于m,n的代数式,由上述条件判断其符号即可.
为什么f(x)是偶函数,可得b=0? 睢宁zhangliang1年前4
睢宁zhangliang1年前4 -
 soso16 共回答了18个问题
soso16 共回答了18个问题 |采纳率83.3%因为,若f(x)是偶函数,则f(x)=f(-x),即ax2+bx+1=ax2-bx+1,即无论x取何值,很有bx=-bx,所以b=0
(1)当b ≠0时,函数为单调递增或递减函数,又x∈R,所以不存在最小值.所以b=0,ax2+1=0
后面的直接解就行了.
怎么这题这么别扭,难道不是正常的考察知识点,而是脑筋急转弯.1年前查看全部
- 在(ax2+bx+1)(2x2-3x-1)的计算结果中,不含x3项和x项,求a,b的值.
 闫安是我1年前2
闫安是我1年前2 -
 飞雨漫天2006 共回答了25个问题
飞雨漫天2006 共回答了25个问题 |采纳率92%解题思路:根据多项式乘以多项式法则展开,合并同类项,根据题意得出2b-3a=0,-3-b=0,求出即可.(ax2+bx+1)(2x2-3x-1)
=2ax4-3ax3-ax2+2bx3-3bx2-bx+2x2-3x-1
=2ax4+(2b-3a)x3+(-a-3b+2)x2+(-3-b)x-1,
∵在(ax2+bx+1)(2x2-3x-1)的计算结果中,不含x3项和x项,
∴2b-3a=0,-3-b=0,
解得:a=-2,b=-3.点评:
本题考点: 多项式乘多项式.
考点点评: 本题考查了多项式乘以多项式法则和二元一次方程组的应用,关键是能根据题意得出关于a、b的方程组.1年前查看全部
- 设函数f(x)=ax2+bx+1(a,b,为实数),F(x)=f(x)(x>0)-f(x)(x<0).
设函数f(x)=ax2+bx+1(a,b,为实数),F(x)=
.f(x)(x>0) -f(x)(x<0)
(1)若f(-1)=0且对任意实数x均有f(x≥0)成立,求F(x)表达式;
(2)在(1)的条件下,当x∈[-3,3]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围. uggm1231年前1
uggm1231年前1 -
 可乐娃娃 共回答了14个问题
可乐娃娃 共回答了14个问题 |采纳率100%解题思路:(1)由f(-1)=0,知b=a+1.由f(x)≥0恒成立,知△=b2-4a=(a+1)2-4a=(a-1)2≤0,由此能求出F(x)表达式.
(2)由f(x)=x2+2x+1,知g(x)=f(x)-kx=x2+(2-k)+1.由于g(x)在[-3,3]上是单调函数,能求出实数k的取值范围.(1)∵f(-1)=0,
∴b=a+1.
由f(x)≥0恒成立,
知△=b2-4a=(a+1)2-4a=(a-1)2≤0,
∴a=1.
从而f(x)=x2+2x+1.
∴F(x)=
(x+1)2(x>0)
-(x+1)2(x<0).
(2)由(1)可知f(x)=x2+2x+1,
∴g(x)=f(x)-kx=x2+(2-k)+1.
由于g(x)在[-3,3]上是单调函数,
知-
2-k
2≤-3或-
2-k
2≥3,
解得k≤-4或k≥8.点评:
本题考点: 函数恒成立问题.
考点点评: 本昰考查函数的恒成立问题,解题时要认真审题,仔细解答,注意合理地进行等价转化.1年前查看全部
- (2010•江津区)如图,抛物线y=ax2+bx+1与x轴交于两点A(-1,0),B(1,0),与y轴交于点C.
 (2010•江津区)如图,抛物线y=ax2+bx+1与x轴交于两点A(-1,0),B(1,0),与y轴交于点C.
(2010•江津区)如图,抛物线y=ax2+bx+1与x轴交于两点A(-1,0),B(1,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)过点B作BD∥CA抛物线交于点D,求四边形ACBD的面积;
(3)在x轴下方的抛物线上是否存在点M,过M作MN⊥x轴于点N,使以A、M、N为顶点的三角形与△BCD相似?若存在,则求出点M的坐标;若不存在,请说明理由. 独孤青心1年前1
独孤青心1年前1 -
 yan200202 共回答了13个问题
yan200202 共回答了13个问题 |采纳率84.6%解题思路:(1)将A、B的坐标代入抛物线的解析式中,即可求出待定系数的值;
(2)先求出直线AC的解析式,由于BD∥AC,那么直线BD的斜率与直线AC的相同,可据此求出直线BD的解析式,联立抛物线的解析式即可求出D点的坐标;由图知四边形ACBD的面积是△ABC和△ABD的面积和,由此可求得其面积;
(3)易知OA=OB=OC=1,那么△ACB是等腰直角三角形,由于AC∥BD,则∠CBD=90°;根据B、C的坐标可求出BC、BD的长,进而可求出它们的比例关系;若以A、M、N为顶点的三角形与△BCD相似,那么两个直角三角形的对应直角边应该成立,可据此求出△AMN两条直角边的比例关系,连接抛物线的解析式即可求出M点的坐标.(1)依题意,得:
a−b+1=0
a+b+1=0,解得
a=−1
b=0;
∴抛物线的解析式为:y=-x2+1;
(2)易知A(-1,0),C(0,1),则直线AC的解析式为:y=x+1;
由于AC∥BD,可设直线BD的解析式为y=x+h,则有:1+h=0,h=-1;
∴直线BD的解析式为y=x-1;联立抛物线的解析式得:
y=−x2+1
y=x−1,解得
x=1
y=0,点评:
本题考点: 二次函数综合题;解二元一次方程组;三角形的面积;勾股定理;相似三角形的判定与性质.
考点点评: 此题主要考查了二次函数解析式的确定、图形面积的求法以及相似三角形的判定和性质等重要知识点,同时还考查了分类讨论的数学思想.1年前查看全部
- (2010•攀枝花二模)已知函数f(x)=ax2+bx+1(a,b∈R).
(2010•攀枝花二模)已知函数f(x)=ax2+bx+1(a,b∈R).
(Ⅰ)若f(-1)=0且对任意实数x均有f(x)≥0成立,求实数a,b的值;
(Ⅱ)在(Ⅰ)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围. wallage1年前1
wallage1年前1 -
 欧洲留zz 共回答了9个问题
欧洲留zz 共回答了9个问题 |采纳率77.8%解题思路:(Ⅰ)由f(-1)=0,可得a-b+1=0即b=a+1,又对任意实数x均有f(x)≥0成立,可得
恒成立,即(a-1)2≤0恒成立,从而可求出a,b的值;a>0 △=b2−4a≤0
(Ⅱ)由(Ⅰ)可知f(x)=x2+2x+1,可得g(x)=x2+(2-k)x+1,由g(x)在x∈[-2,2]时是单调函数,可得[−2,2]⊂(−∞,
]或[−2,2]⊂[k−2 2
,+∞),从而得出2≤k−2 2
或k−2 2
≤−2,解之即可得出k的取值范围.k−2 2 (Ⅰ)∵f(-1)=0,
∴a-b+1=0即b=a+1,
又对任意实数x均有f(x)≥0成立
∴
a>0
△=b2−4a≤0恒成立,即(a-1)2≤0恒成立
∴a=1,b=2;
(Ⅱ)由(Ⅰ)可知f(x)=x2+2x+1
∴g(x)=x2+(2-k)x+1
∵g(x)在x∈[-2,2]时是单调函数,
∴[−2,2]⊂(−∞,
k−2
2]或[−2,2]⊂[
k−2
2,+∞)
∴2≤
k−2
2或
k−2
2≤−2,
即实数k的取值范围为(-∞,-2]∪[6,+∞).点评:
本题考点: 函数恒成立问题;函数单调性的性质.
考点点评: 本题考查了函数的恒成立问题及函数单调性的应用,难度一般,关键是掌握函数单调性的应用.1年前查看全部
- 给出三个命题:①点P(b,a)在抛物线y=x2+1上;②点A(1,3)能在抛物线y=ax2+bx+1上;③点B(-2,1
给出三个命题:①点P(b,a)在抛物线y=x2+1上;②点A(1,3)能在抛物线y=ax2+bx+1上;③点B(-2,1)能在抛物线y=ax2-bx+1上.若①为真命题,则( )
A. ②③都是真命题
B. ②③都是假命题
C. ②是真命题,③是假命题
D. ②是假命题,③是真命题 mk198110061年前3
mk198110061年前3 -
 95585 共回答了20个问题
95585 共回答了20个问题 |采纳率95%解题思路:分析是否为真命题,需要分别分析各题设是否能推出结论.根据题意,得
把点P(b,a)代入抛物线y=x2+1,得a=b2+1.
②中,把点A(1,3)代入抛物线y=ax2+bx+1,得a+b+1=3.
把a=b2+1,代入得b2+b-1=0,
△=1+4=5>0,则方程有解.
故原命题为真命题.
③中,把点B(-2,1)代入抛物线y=ax2-bx+1,得a(-2)2-b×(-2)+1=1,即4a+2b=0.
把a=b2+1代入,得4b2+4+2b=0,
△=4-4×4×4=-60<0,则方程无解.
故原命题为假命题.
故选C.点评:
本题考点: 命题与定理.
考点点评: 解答此题的关键是要熟知真命题与假命题的概念:
真命题:判断正确的命题叫真命题;
假命题:判断错误的命题叫假命题;1年前查看全部
- 设函数f(x)=ax2+bx+1(a,b属于R).若f(-1)=0且对任意实数f(x)>=0恒成立,求f(x)的表达式
 闻啼鸟的声音1年前4
闻啼鸟的声音1年前4 -
 kathy_s 共回答了29个问题
kathy_s 共回答了29个问题 |采纳率79.3%1、因为任意实数x,f(x)≥0恒成立,所以a>0.△=0
又因为f(-1)=0,所以有 a-b+1=0,b^2-4a=0,解出a=1,b=2
所以f(x)=x^2+2x+1(这个问题中条件任意实数x,f(x)≥0恒成立,应理解为一个二次函数的值域为≥0时,只能是开口向上,且与x轴只有一个交点,这样才能有足够的条件求解a,b)
2、g(x)=x^2+(2-k)x+1,因为当x∈[-2,2]时,g(x)=f(x)-kx是单调函数
所以(k-2)/2≥2,k≥61年前查看全部
- 已知二次函数f(x)=ax2+bx+1(a>0),若f(-1)=0,且对任意实数x均有f(x)≥0成立.且F(x)=f(
已知二次函数f(x)=ax2+bx+1(a>0),若f(-1)=0,且对任意实数x均有f(x)≥0成立.且F(x)=
f(x)(x>0) -f(x)(x<0)
(Ⅰ)求F(x)的表达式;
(Ⅱ)若当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求k的取值范围. 是个粗人1年前1
是个粗人1年前1 -
 phrankie 共回答了15个问题
phrankie 共回答了15个问题 |采纳率86.7%解题思路:(I)二次函数过点(-1,0)代入求出a与b的关系式,减少未知量,再根据任意实数x均有f(x)≥0成立,a>0,开口向上,可得△≤0,从而求解出a的范围,得到a值,再写出F(x);
(II)由(I)可知f(x)的解析式,代入g(x),然后对g(x)进行求导,利用常数分离法求出k的取值范围;(I)∵二次函数f(x)=ax2+bx+1(a>0),且f(-1)=0,∴a-b+1=0,得b=a+1,则f(x)=ax2+(a+1)x+1,又∵对任意实数x均有f(x)≥0成立,a>0,∴△=(a+1)2-4a≤0,即(a-1)2≤0,∴a=1,∴f(x)=x2+2x+1,...
点评:
本题考点: 函数单调性的性质;函数解析式的求解及常用方法.
考点点评: 本题考查了函数的单调性的应用,两个函数的简单运算后判定单调性,解题过程中用到了常数分离法求范围的方法,这是高考常考的考点,我们要熟练掌握;1年前查看全部
- 已知抛物线y=ax2+bx+1的大致位置如图所示,那么直线y=ax+b不经过( )
 已知抛物线y=ax2+bx+1的大致位置如图所示,那么直线y=ax+b不经过( )
已知抛物线y=ax2+bx+1的大致位置如图所示,那么直线y=ax+b不经过( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限 爱上你的我29011年前1
爱上你的我29011年前1 -
 梅克尼斯 共回答了24个问题
梅克尼斯 共回答了24个问题 |采纳率95.8%解题思路:根据二次函数图象开口向下可得a<0,再根据二次函数图象的对称轴求出b的取值范围,然后根据一次函数图象的性质作出判断即可.∵抛物线开口向下,
∴a<0,
∵抛物线对称轴在y轴的左边,
∴-[b/2a]<0,
解得b<0,
∴直线y=ax+b的图象经过第二、四象限,且与y轴负半轴相交,不经过第一象限.
故选A.点评:
本题考点: 二次函数的图象;一次函数图象与系数的关系.
考点点评: 本题考查了二次函数图象与一次函数图象与系数的关系,根据抛物线确定出a、b的取值范围是解题的关键,也是难点.1年前查看全部
- 已知函数f(x)=ax2+bx+1(1)若f(x)>0的解集是{x|x4}求实数a ,b的值(2)若f(–1)=1且f(
已知函数f(x)=ax2+bx+1(1)若f(x)>0的解集是{x|x4}求实数a ,b的值(2)若f(–1)=1且f(x)
 双清1年前0
双清1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 设函数f(x)=ax2+bx+1(a、b∈R),若b=a+1,对任意的a∈[-1,1]都有f(x)≥0成立,求x取值范围
设函数f(x)=ax2+bx+1(a、b∈R),若b=a+1,对任意的a∈[-1,1]都有f(x)≥0成立,求x取值范围.
 账多不愁11年前1
账多不愁11年前1 -
 cgh115 共回答了18个问题
cgh115 共回答了18个问题 |采纳率94.4%解题思路:当x=0或-1时,满足条件.当x≠0 且x≠-1时,则有x2+x≠0,再由
,求得x的范围.(x2+1)•(−1)+x+1≥0 (x2+1)+x+1≥0 由题意可得,f(x)=ax2+(a+1)x+1=(x2+x)a+(x+1),显然,当x=0或-1时,满足对任意的a∈[-1,1]都有f(x)≥0成立.
当x≠0 且x≠-1时,则有x2+x≠0,再由
(x2+1)•(−1)+x+1≥0
(x2+1)+x+1≥0,求得0≤x≤1.点评:
本题考点: 二次函数在闭区间上的最值.
考点点评: 本题主要考查求二次函数在闭区间上的最值,二次函数的性质的应用,体现了转化的数学思想,属基础题.1年前查看全部
- 若二次函数f(x)=ax2+bx+1(a,b为实数且x∈R).
若二次函数f(x)=ax2+bx+1(a,b为实数且x∈R).
(1)若函数f(x)为偶函数,且满足f(x)=2x有两个相等实根,求a,b的值;
(2)若f(-1)=0,且函数f(x)的值域为[0,+∞),求函数f(x)的表达式;
(3)在(2)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围. 艾寻心1年前1
艾寻心1年前1 -
 逃走的水蒸气 共回答了24个问题
逃走的水蒸气 共回答了24个问题 |采纳率79.2%解题思路:(1)利用函数f(x)为偶函数,求出b,利用f(x)=2x有两个相等实根,△=0,求出a,即可得到a,b的值;
(2)若f(-1)=0,推出a,b的一个关系式,利用函数f(x)的值域为[0,+∞),得到a,b,的关系式,然后求a,b,得到函数f(x)的表达式;
(3)通过(2)的条件,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,利用二次函数的对称轴,求实数k的取值范围.(1)因为函数是偶函数,所以b=0,因为f(x)=2x有两个相等实根,即ax2+1=2x.有△=0,所以a=1.(2)∵f(-1)=0,∴a-b+1=0,又x∈R,f(x)≥0恒成立.∴a>0△=b2−4a≤0,∴b2-4(b-1)≤0,∴b=2,a=1,∴f(...
点评:
本题考点: 一元二次方程的根的分布与系数的关系;函数奇偶性的性质;二次函数的性质.
考点点评: 本题考查一元二次方程的根的分布与系数的关系,函数奇偶性的性质,二次函数的性质的应用,考查计算能力.1年前查看全部
- 在(ax2+bx+1)(2x2-3x-1)的计算结果中,不含x3项和x项,求a,b的值.
 iamxiaoling1年前1
iamxiaoling1年前1 -
 伤痕垒垒 共回答了22个问题
伤痕垒垒 共回答了22个问题 |采纳率95.5%解题思路:根据多项式乘以多项式法则展开,合并同类项,根据题意得出2b-3a=0,-3-b=0,求出即可.(ax2+bx+1)(2x2-3x-1)
=2ax4-3ax3-ax2+2bx3-3bx2-bx+2x2-3x-1
=2ax4+(2b-3a)x3+(-a-3b+2)x2+(-3-b)x-1,
∵在(ax2+bx+1)(2x2-3x-1)的计算结果中,不含x3项和x项,
∴2b-3a=0,-3-b=0,
解得:a=-2,b=-3.点评:
本题考点: 多项式乘多项式.
考点点评: 本题考查了多项式乘以多项式法则和二元一次方程组的应用,关键是能根据题意得出关于a、b的方程组.1年前查看全部
- 已知函数f(x)=ax2+bx+1(a,b∈R).
已知函数f(x)=ax2+bx+1(a,b∈R).
(Ⅰ)若f(-1)=0且对任意实数x均有f(x)≥0成立,求实数a,b的值;
(Ⅱ)在(Ⅰ)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围. 北区店小二1年前0
北区店小二1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 已知函数f(x)=ax2+bx+1(a,b为实数,a≠0,x∈R),若f(-1)=0,且函数f(x)的值域为[0,+∞)
已知函数f(x)=ax2+bx+1(a,b为实数,a≠0,x∈R),若f(-1)=0,且函数f(x)的值域为[0,+∞),
(1)求f(x)的表达式;
(2)当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围. 皖人1年前0
皖人1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 函数f(x)=ax2+bx+1(a>0)(1)若f(-1)=0,并对x∈R恒有f(x)≥0,求f(x)的表达式;(2)在
函数f(x)=ax2+bx+1(a>0)(1)若f(-1)=0,并对x∈R恒有f(x)≥0,求f(x)的表达式;(2)在(1)的条件下,对x∈[-1,1],g(x)=f(x)-kx是单调函数,求k的范围.
 蓝色ll球1年前1
蓝色ll球1年前1 -
 zwctl_111 共回答了16个问题
zwctl_111 共回答了16个问题 |采纳率100%解题思路:(1)由 f(-1)=0得a-b+1=0,又因为对x∈R恒有f(x)≥0,△=b2-4a≤0,得(a+1)2-4a≤0,从而求出a,b的值.
(2)首先表示出g(x)=x2+(2-k)x+1,根据单调故应满足
≥1或k−2 2
≤−1,从而求出k的取值范围.k−2 2 (1)由 f(-1)=0得a-b+1=0又因为对x∈R恒有f(x)≥0,△=b2-4a≤0,得(a+1)2-4a≤0,(a-1)2≤0,
所以a=1b=2得f(x)=x2+2x+1
(2)g(x)=f(x)-kx=x2+(2-k)x+1是单调函数,则
k−2
2≥1或
k−2
2≤−1,所以得k≥4或k≤0点评:
本题考点: 二次函数的性质;函数单调性的性质.
考点点评: 本题考查了二次函数的性质,主要是单调性的应用,属于基础重点题型,应该熟练掌握.1年前查看全部
- 已知函数f(x)=ax2+bx+1(a≠0)对于任意x∈R都有f(1+x)=f(1-x),且函数y=f(x)+2x为偶函
已知函数f(x)=ax2+bx+1(a≠0)对于任意x∈R都有f(1+x)=f(1-x),且函数y=f(x)+2x为偶函数;函数g(x)=1-2x.
(Ⅰ)求函数f(x)的表达式;
(Ⅱ)求证:方程f(x)+g(x)=0在区间[0,1]上有唯一实数根;
(Ⅲ)若有f(m)=g(n),求实数n的取值范围. bjoo1年前1
bjoo1年前1 -
 帆安 共回答了11个问题
帆安 共回答了11个问题 |采纳率81.8%解题思路:(I)根据对于任意x∈R都有f(1+x)=f(1-x)可知对称轴为x=1,由此得a,b的方程,再由y=f(x)+2x为偶函数可求得b值,从而求得a值;
(II)设h(x)=f(x)+g(x),方程f(x)+g(x)=0在区间[0,1]上有唯一实数根转化为证明函数h(x)在[0,1]上有唯一零点,根据零点存在定理判定其存在性,利用单调性判定其唯一性;
(III)求出f(x),g(x)的值域及其交集,据f(m)=g(n)知g(n)属于该交集;(I)∵对于任意x∈R都有f(1+x)=f(1-x),
∴函数f(x)的对称轴为x=1,得b=-2a.
又函数y=f(x)+2x=ax2+(b+2)x+1为偶函数,
∴b=-2,从而可得a=1.
∴f(x)=x2-2x+1=(x-1)2.
(II)证明:设h(x)=f(x)+g(x)=(x-1)2+1-2x,
∵h(0)=2-20=1>0,h(1)=-1<0,
∴h(0)h(1)<0.
∴函数h(x)在区间[0,1]内必有零点,
又∵(x-1)2,-2x在区间[0,1]上均单调递减,
所以h(x)在区间[0,1]上单调递减,
∴h(x)在区间[0,1]上存在唯一零点.
故方程f(x)+g(x)=0在区间[0,1]上有唯一实数根.
(III)由题可知∴f(x)=(x-1)2≥0.g(x)=1-2x<1,
若有f(m)=g(n),则g(n)∈[0,1),
则1-2n≥0,解得 n≤0.
故n的取值范围是n≤0.点评:
本题考点: 根的存在性及根的个数判断;函数奇偶性的性质.
考点点评: 本题考查根的存在性及根的个数判断,考查函数奇偶性的性质,考查学生对问题的理解能力及转化能力,零点存在定理及二次函数的有关性质是解决问题的基础.1年前查看全部
- F(x)是奇函数f(x)=(ax2+bx+1)%(cx+d)x>0F(X)最小值为2根号2f(1)=3求f(X)
 applematrix1年前2
applematrix1年前2 -
 fsonic 共回答了25个问题
fsonic 共回答了25个问题 |采纳率96%请问那个百分号是指啥,奇函数关于原点对称即f(x)=-f(-x),代入上式计算1年前查看全部
- 一元二次函数f(x)=ax2+bx+1(a,b∈R),x∈R,若函数f(x)的最小值为f(-1)=0,求f(x)的解析式
一元二次函数f(x)=ax2+bx+1(a,b∈R),x∈R,若函数f(x)的最小值为f(-1)=0,求f(x)的解析式并写出单调区间.
 jw11831年前1
jw11831年前1 -
 专治古路木 共回答了17个问题
专治古路木 共回答了17个问题 |采纳率100%解题思路:本题通过二次函数的顶点坐标,得到参数a,b的方程,从而求出a,b的值,得到函数的解析式,再利用图象特征,得到函数的单调区间.∵二次函数f(x)=ax2+bx+1的最小值为f(-1)=0,
∴
a>0
−
b
2a=−1
4a−b2
4a=0,
∴
a=1
b=2,
∴f(x)=x2+2x+1.
在区间(-∞,-1)单调递减,在区间[-1,+∞)单调递增.
∴f(x)的解析式为f(x)=x2+2x+1.单调减区间为(-∞,-1),单调增区间为[-1,+∞).点评:
本题考点: 函数解析式的求解及常用方法;函数单调性的判断与证明.
考点点评: 本题考查了二次函数的解析式和单调性,本题还可以用二次函数的顶点式去研究.本题难度不大,属于基础题.1年前查看全部
- 已知ax2+bx+1与3x+1的积不含x3的项,也不含x的项,那么a=______,b=______.
 胡说十八拍1年前3
胡说十八拍1年前3 -
 绝种男人 共回答了23个问题
绝种男人 共回答了23个问题 |采纳率91.3%解题思路:由题意列出算式,利用多项式乘以多项式法则计算,合并后令三次项与一次项系数为0,即可求出a与b的值.根据题意列得:(ax2+bx+1)(3x+1)=3ax3+(a+3b)x2+(b+3)x+1,
∵不含x3的项,也不含x的项,
∴3a=0,b+3=0,
则a=0,b=-3.
故答案为:0;-3点评:
本题考点: 多项式乘多项式.
考点点评: 此题考查了多项式乘以多项式,熟练掌握多项式乘以多项式法则是解本题的关键.1年前查看全部
- 当x=1时,代数式ax2+bx+1的值是3,则(a+b-1)(1-a-b)的值等于______.
 千娇春1年前1
千娇春1年前1 -
 我在书馆 共回答了19个问题
我在书馆 共回答了19个问题 |采纳率94.7%解题思路:由x=1时,代数式ax2+bx+1的值是3,求出a+b的值,将所得的值代入所求的代数式中进行计算即可得解.由题意知:a+b+1=3,
∴a+b=2,
∴(a+b-1)(1-a-b)=(2-1)×(1-2)=-1.故答案填-1.点评:
本题考点: 代数式求值.
考点点评: 本题主要考查代数式的求值,注意运用整体代入法求解.1年前查看全部
- 已知二次函数f(x)=ax2+bx+1的导函数为f′(x),f′(0)>0,f(x)与x轴恰有一个交点,则f(1)f′(
已知二次函数f(x)=ax2+bx+1的导函数为f′(x),f′(0)>0,f(x)与x轴恰有一个交点,则
的最小值为______.f(1) f′(0)  obddj7af1年前1
obddj7af1年前1 -
 hisam 共回答了24个问题
hisam 共回答了24个问题 |采纳率83.3%解题思路:首先对f(x)求导,得出f′(x)=2ax+b,再利用f′(0)>0,可得出b>0;利用f(x)与x轴恰有一个交点,可得出△=0,得到a与b的关系式,即可用a表示b,从而得出
的关于b表达式,再利用基本不等式即可求出其最小值.f(1) f′(0) ∵f(x)=ax2+bx+1,∴f′(x)=2ax+b,∴f′(0)=b,又f′(0)>0,∴b>0.
又已知f(x)与x轴恰有一个交点,∴△=b2-4a=0,∴a=
b2
4,
∴f(1)=a+b+1=
b2
4+b+1.
∴
f(1)
f′(0)=
b2
4+b+1
b=
b
4+
1
b+1≥2
b
4×
1
b+1=1+1=2.当且仅当[b/4=
1
b],即b=2时取等号,
∴最小值为2.
故答案为2.点评:
本题考点: 导数的运算;函数的零点.
考点点评: 本题综合考查了二次函数、导数、基本不等式,熟练掌握它们的性质及使用方法是解决问题的关键,此题为中档题.1年前查看全部
- 已知二次函数f(x)=ax2+bx+1和函数g(x)=bx-1a2x+2b,方程g(x)=x有两个不等非零实根x1、x2
已知二次函数f(x)=ax2+bx+1和函数g(x)=
,方程g(x)=x有两个不等非零实根x1、x2(x1<x2).bx-1 a2x+2b
(1)证明函数f(x)在(-1,1)上是单调函数;
(2)若方程f(x)=0的两实根为x3,x4(x3<x4),求使x3<x1<x2<x4成立的a的取值范围. phc07141年前1
phc07141年前1 -
 cym015 共回答了21个问题
cym015 共回答了21个问题 |采纳率81%(1)由g(x)=
bx-1
a2x+2b=x⇒方程a2x2+bx+1=0(*)有不等实根∴△=b2-4a2>0及a≠0,⇒|
b
2a|>1,即-
b
2a<-1,或-
b
2a>1
又f(x)的对称轴x=-
b
2a∉(-1,1)
故f(x)在(-1,1)上是单调函数
(2)因x1、x2是方程(*)的根,∴a2x12+bx1+1=0∴bx1=-a2x12-1
同理bx2=-a2x22-1∴f(x1)=ax12+b1x1+1=ax12-a2x12+1=(a-a2)x12,同理f(x2)=(a-a2)x22
要使x3<x1<x2<x4,只需
a>0
f(x1)<0
f(x2)<0⇒
a>0
a-a2<0⇒a>1
或
a<0
f(x1)>0
f(x2)>0⇒
a<0
a-a2>0⇒ϕ
故a的取值范围a>11年前查看全部
- 已知函数f(x)=ax2+bx+1(a,b为实数),x∈R,
已知函数f(x)=ax2+bx+1(a,b为实数),x∈R,
(1)若f(x)有一个零点为-1,且函数f(x)的值域为[0,+∞),求f(x)的解析式;
(2)在(1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围. 伟大滴米虫1年前4
伟大滴米虫1年前4 -
 kdwn 共回答了11个问题
kdwn 共回答了11个问题 |采纳率90.9%解题思路:(1)由f(-1)=0,可得a-b+1=0,又函数f(x)的值域为[0,+∞),可得二次函数的对称轴,从而可求出a,b的值;
(2)由(1)可知f(x)=x2+2x+1,可得g(x)=x2+(2-k)x+1,由g(x)在x∈[-2,2]时是单调函数,可得[−2,2]⊂(−∞,
]或[−2,2]⊂[k−2 2
,+∞),从而得出2≤k−2 2
或k−2 2
≤−2,解之即可得出k的取值范围.k−2 2 (1)由题意得:
a−b+1=0
−
b
2a=−1解得:
a=1
b=2
所以:f(x)=x2+2x+1…(6分)
(2)由(1)得g(x)=x2+(2-k)x+1当x∈[-2,2]时,g(x)是单调函数的充要条件是:
[−2,2]⊂(−∞,
k−2
2]或[−2,2]⊂[
k−2
2,+∞),
-[2−k/2]≥2或−
2−k
2≤−2
解得:k≥6或k≤-2…(12分)点评:
本题考点: 二次函数的性质.
考点点评: 本题考查了函数的恒成立问题及函数单调性的应用,难度一般,关键是掌握函数单调性的应用.1年前查看全部
- f(x)=ax2+bx+1(ab属于R且a>0)有两个零点.其中一个零点在区间(1,2)内,则a-b的取值范围是?
f(x)=ax2+bx+1(ab属于R且a>0)有两个零点.其中一个零点在区间(1,2)内,则a-b的取值范围是?
拜托各路数学高手~~~~~~~~~ 西北狼子1年前1
西北狼子1年前1 -
 qqqqqq1973 共回答了16个问题
qqqqqq1973 共回答了16个问题 |采纳率100%不大想动笔算.你求出原方程的两点零点,然后根据零点区间算,算不出来?1年前查看全部
- 一元二次函数f(x)=ax2+bx+1(a,b∈R),x∈R,若函数f(x)的最小值为f(-1)=0,求f(x)的解析式
一元二次函数f(x)=ax2+bx+1(a,b∈R),x∈R,若函数f(x)的最小值为f(-1)=0,求f(x)的解析式并写出单调区间.
 justlove19831年前3
justlove19831年前3 -
 huer_gao 共回答了18个问题
huer_gao 共回答了18个问题 |采纳率94.4%解题思路:本题通过二次函数的顶点坐标,得到参数a,b的方程,从而求出a,b的值,得到函数的解析式,再利用图象特征,得到函数的单调区间.∵二次函数f(x)=ax2+bx+1的最小值为f(-1)=0,
∴
a>0
−
b
2a=−1
4a−b2
4a=0,
∴
a=1
b=2,
∴f(x)=x2+2x+1.
在区间(-∞,-1)单调递减,在区间[-1,+∞)单调递增.
∴f(x)的解析式为f(x)=x2+2x+1.单调减区间为(-∞,-1),单调增区间为[-1,+∞).点评:
本题考点: 函数解析式的求解及常用方法;函数单调性的判断与证明.
考点点评: 本题考查了二次函数的解析式和单调性,本题还可以用二次函数的顶点式去研究.本题难度不大,属于基础题.1年前查看全部
- 已知二次函数f(x)=ax2+bx+1(a>0,b∈R),方程f(x)=x有两个实数根x1、x2.
已知二次函数f(x)=ax2+bx+1(a>0,b∈R),方程f(x)=x有两个实数根x1、x2.
(Ⅰ)如果x1<2<x2<4,设函数f(x)的对称轴为x=x0,求证x0>-1;
(Ⅱ)如果0<x1<2,且f(x)=x的两实根相差为2,求实数b的取值范围. zdj9011年前0
zdj9011年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 当x=1时,代数式ax2+bx+1的值是3,则(a+b-1)(1-a-b)的值等于______.
 下午二点吃早餐1年前4
下午二点吃早餐1年前4 -
 今试回头 共回答了21个问题
今试回头 共回答了21个问题 |采纳率85.7%解题思路:由x=1时,代数式ax2+bx+1的值是3,求出a+b的值,将所得的值代入所求的代数式中进行计算即可得解.由题意知:a+b+1=3,
∴a+b=2,
∴(a+b-1)(1-a-b)=(2-1)×(1-2)=-1.故答案填-1.点评:
本题考点: 代数式求值.
考点点评: 本题主要考查代数式的求值,注意运用整体代入法求解.1年前查看全部
- 已知ax2+bx+1与2x2-3x+1的积不含x3和x项,试计算下面代数式的值.[1(a−1)(b−1)+1/ab+1(
已知ax2+bx+1与2x2-3x+1的积不含x3和x项,试计算下面代数式的值.[1
(a−1)(b−1)
+1/ab
+1 (a+1)(b+1)
+…+1 (a+2)(b+2) 1 (a+2010)(b+2010)]. 赞
魅力珠儿 幼苗
共回答了16个问题采纳率:81.3% 举报
(ax2+bx+1)•(2x2-3x+1),
=2ax4-3ax3+ax2+2bx3-3bx2+bx+2x2-3x+1,
=2ax4+(-3a+2b)x3+(a-3b+2)x2+(b-3)x+1,
∵不含x3和x项,
∴b-3=0,-3a+2b=0,
∴b=3,a=2,
把a=2,b=3代入得:
[1
(a−1)(b−1)+
1/ab+
1
(a+1)(b+1)+
1
(a+2)(b+2)+…+
1
(a+2010)(b+2010)]
=[1/1×2]+[1/2×3]+[1/3×4]+[1/4×5]+…+[1/2012×2013]
=[1/1]-[1/2]+[1/2]-[1/3]+[1/3]-[1/4]+[1/4]-[1/5]+…+[1/2012]-[1/2013]
=1-[1/2013]
=[2012/2013].1年前
4可能相似的问题-
已知二次三项式ax²+bx+1与2x²-3x+1的积不含x³项,
1年前1个回答
你能帮帮他们吗
Copyright © 2022 YULUCN.COM - 雨露学习互助 - 17 q. 0.028 s. - webmaster@yulucn.com 恋恋情歌1年前1
恋恋情歌1年前1 -
 魅力珠儿 共回答了16个问题
魅力珠儿 共回答了16个问题 |采纳率81.3%(ax2+bx+1)•(2x2-3x+1),
=2ax4-3ax3+ax2+2bx3-3bx2+bx+2x2-3x+1,
=2ax4+(-3a+2b)x3+(a-3b+2)x2+(b-3)x+1,
∵不含x3和x项,
∴b-3=0,-3a+2b=0,
∴b=3,a=2,
把a=2,b=3代入得:
[1
(a−1)(b−1)+
1/ab+
1
(a+1)(b+1)+
1
(a+2)(b+2)+…+
1
(a+2010)(b+2010)]
=[1/1×2]+[1/2×3]+[1/3×4]+[1/4×5]+…+[1/2012×2013]
=[1/1]-[1/2]+[1/2]-[1/3]+[1/3]-[1/4]+[1/4]-[1/5]+…+[1/2012]-[1/2013]
=1-[1/2013]
=[2012/2013].1年前查看全部
- 高一数学竞赛预赛试题抛物线y=ax2+bx+1的参数a,b满足8a2+4ab=b3,则当a,b变动时,抛物线的顶点一定在
高一数学竞赛预赛试题
抛物线y=ax2+bx+1的参数a,b满足8a2+4ab=b3,则当a,b变动时,抛物线的顶点一定在()上.
(A)抛物线(B)双曲线(C)圆或椭圆(D)直线
答案是c.为什么?
shiB hdc46391年前4
hdc46391年前4 -
 静8静 共回答了22个问题
静8静 共回答了22个问题 |采纳率95.5%挺简单,你只要先写出顶点坐标,再利用8a2+4ab=b3,代换掉顶点坐标中的(4a-b2),再消参即可,再告你一句,你如果学了圆锥曲线很容易就能把此题搞定,否则你还是不要做了1年前查看全部
- 已知二次函数f(x)=ax2+bx+1的导函数为f′(x),f′(0)>0,f(x)与x轴恰有一个交点,则f(1)f′(
已知二次函数f(x)=ax2+bx+1的导函数为f′(x),f′(0)>0,f(x)与x轴恰有一个交点,则
的最小值为______.f(1) f′(0)  五儿_pixy1年前4
五儿_pixy1年前4 -
 窝头三个半 共回答了17个问题
窝头三个半 共回答了17个问题 |采纳率100%解题思路:首先对f(x)求导,得出f′(x)=2ax+b,再利用f′(0)>0,可得出b>0;利用f(x)与x轴恰有一个交点,可得出△=0,得到a与b的关系式,即可用a表示b,从而得出
的关于b表达式,再利用基本不等式即可求出其最小值.f(1) f′(0) ∵f(x)=ax2+bx+1,∴f′(x)=2ax+b,∴f′(0)=b,又f′(0)>0,∴b>0.
又已知f(x)与x轴恰有一个交点,∴△=b2-4a=0,∴a=
b2
4,
∴f(1)=a+b+1=
b2
4+b+1.
∴
f(1)
f′(0)=
b2
4+b+1
b=
b
4+
1
b+1≥2
b
4×
1
b+1=1+1=2.当且仅当[b/4=
1
b],即b=2时取等号,
∴最小值为2.
故答案为2.点评:
本题考点: 导数的运算;函数的零点.
考点点评: 本题综合考查了二次函数、导数、基本不等式,熟练掌握它们的性质及使用方法是解决问题的关键,此题为中档题.1年前查看全部
- (2012•泸州模拟)已知函数f(x)=ax2+bx+1(a、b为实数),若f(-1)=0且函数f(x)的值域为[0,+
(2012•泸州模拟)已知函数f(x)=ax2+bx+1(a、b为实数),若f(-1)=0且函数f(x)的值域为[0,+∞).
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)设F(x)=xf(x),求曲线F(x)在x=1处的切线方程. 子飞在线1年前1
子飞在线1年前1 -
 514330 共回答了16个问题
514330 共回答了16个问题 |采纳率100%解题思路:(Ⅰ)根据f(-1)=0可得a-b+1=0①又函数f(x)的值域为[0,+∞)可分析出a>0故可将f(x)=ax2+bx+1变形为f(x)=a(x+
)2+b 2a
故y≥4a−b2 4a
所以4a-b2=0②,然后由①②即可求出a,b的值从而求出f(x).4a−b2 4a
(Ⅱ)根据F(x)=xf(x)可求出F(x)的解析式再根据导数的几何意义可得曲线F(x)在x=1处的切线方程的斜率为F′(1)然后再根据点斜式写出切线方程即可.(Ⅰ)∵f(-1)=0∴a-b+1=0①又函数f(x)的值域为[0,+∞)∴a>0∵f(x)=ax2+bx+1=a(x+b2a)2+4a−b24a∴y≥4a−b24a∴4a-b2=0②由①②得:a=1,b=2∴f(x)=x2+2x+1(Ⅱ)∵F(x)=xf(x)∴F′(x)=3x2+4x+1∴...
点评:
本题考点: 利用导数研究曲线上某点切线方程;函数解析式的求解及常用方法;二次函数的性质.
考点点评: 本题主要考查了利用导数的几何意义研究在某点处的切线方程,属常考题,较难.解题的关键是根据导数的几何意义得出F′(1)即为曲线F(x)在x=1处的切线方程的斜率!1年前查看全部
- (第一、二层次学校的学生做)对于函数f(x)=ax2+bx+1(a>0),如果方程f(x)=x有相异两根x1,x2.(1
(第一、二层次学校的学生做)
对于函数f(x)=ax2+bx+1(a>0),如果方程f(x)=x有相异两根x1,x2.
(1)若x1<1<x2,且f(x)的图象关于直线x=m对称.求证:m>
;1 2
(2)若0<x1<2且|x1-x2|=2,求证:4a+2b<1;
(3)α、β为区间[x1,x2]上的两个不同的点,求证:2aαβ-(1-b)(a+β)+2<0. emzy1年前1
emzy1年前1 -
 忧郁猪宝贝 共回答了19个问题
忧郁猪宝贝 共回答了19个问题 |采纳率84.2%解题思路:(1)根据题意,x1、x2是方程g(x)=f(x)-x=0的两个实数根,由x1<1<x2可得g(1)<0,证出x1x2<x1+x2-1.由此结合x=m满足m=[1/2](-[b−1/a]-[1/a]),将其化简成关于x1、x2的式子即可证出m>
;1 2
(2)由方程g(x)=0,结合根与系数的关系算出x1x2=[1/a]>0,故x1、x2同号.结合题意0<x1<2且|x1-x2|=2,证出x2=x1+2>2,从而得到2∈(x1,x2),由g(2)<0,即可证出4a+2b<1;
(3)由前面结论得x1+x2=[−b+1/a],x1x2=[1/a].设α<β,将2(α-x1)(β-x2)展开化简,进行配凑得2(α-x1)(β-x2)>2αβ-(x1+x2)(α+β)+2x1x2,结合2αβ-(x1+x2)(α+β)+2x1x2=
,可得2aαβ−(1−b)(α−β)+2 a
<0,结合a>0即可得到原不等式成立.2aαβ−(1−b)(α−β)+2 a (1)设g(x)=ax2+(b-1)x+1,且a>0
∵x1<1<x2,∴(x1-1)(x2-1)<0,即x1x2<x1+x2-1,
于是x=m即x=-[b/2a],也就是x=[1/2](-[b−1/a]-[1/a])
∴m=[1/2](-[b−1/a]-[1/a])=[1/2](x1+x2)-[1/2]x1x2>[1/2](x1+x2)-[1/2][(x1+x2)-1]=[1/2]
即不等式m>
1
2成立;
(2)由方程g(x)=ax2+(b-1)x+1=0,可得x1x2=[1/a]>0,故x1、x2同号
由0<x1<2且|x1-x2|=2,得x2-x1=2
∴x2=x1+2>2,
由此可得2∈(x1,x2),得g(2)<0,
所以4a+2b-1<0,可得4a+2b<1;
(3)由前面的结论,得x1+x2=[−b+1/a],x1x2=[1/a]
α、β为区间[x1,x2]上的两个不同的点,不妨设α<β
0>2(α-x1)(β-x2)
∵2(α-x1)(β-x2)=2αβ-2(βx1+αx2)+2x1x2
=2αβ-(x1+x2)(α+β)+2x1x2+(x1-x2)(α-β)>2αβ-(x1+x2)(α+β)+2x1x2
且2αβ-(x1+x2)(α+β)+2x1x2=
2aαβ−(1−b)(α−β)+2
a
∴0>
2aαβ−(1−b)(α−β)+2
a,
结合a>0,可得2aαβ-(1-b)(a+β)+2<0.点评:
本题考点: 一元二次方程的根的分布与系数的关系;二次函数的性质.
考点点评: 本题给出二次函数满足的条件,求证不等式恒成立并讨论函数零点的分布.着重考查了一元二次方程根与系数的关系、函数的零点和不等式的等价变形等知识,考查了逻辑思维能力与推理论证能力,考查了转化化归与数形结合的数学思想,属于难题.1年前查看全部
- (2k14•市中区二模)二次函数y=ax2+bx+1(a≠k)k图象如图,下列结论中,正确结论k有( )个.
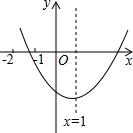 (2k14•市中区二模)二次函数y=ax2+bx+1(a≠k)k图象如图,下列结论中,正确结论k有( )个.
(2k14•市中区二模)二次函数y=ax2+bx+1(a≠k)k图象如图,下列结论中,正确结论k有( )个.
①b2-4a1>k;②ab1>k;③8a+1>k;④9a+3b+1<k.
A.1
B.2
C.3
D.4 荆门大战1年前1
荆门大战1年前1 -
 金面佛牙 共回答了24个问题
金面佛牙 共回答了24个问题 |采纳率91.7%解题思路:由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及x=-1时二次函数的值的情况进行推理,进而对所得结论进行判断.①由图知:抛物线与x轴有两个不同的交点,则△=b2-4ac>0,故①正确;
②抛物线开口向上,得:a>0;
抛物线的对称轴为x=-[b/2a]=1,b=-2a,故b<0;
抛物线交y轴于负半轴,得:c<0;
所以abc>0;
故②正确;
③根据②可将抛物线的解析式化为:y=ax2-2ax+c(a≠0);
由函数的图象知:当x=-2时,y>0;即4a-(-4a)+c=8a+c>0,故③正确;
④根据抛物线的对称轴方程可知:(-1,0)关于对称轴的对称点是(3,0);
当x=-1时,y<0,所以当x=3时,也有y<0,即9a+3b+c<0;故④正确;
所以这四个结论都正确.
故选D.点评:
本题考点: 二次函数图象与系数的关系.
考点点评: 本题主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.1年前查看全部
大家在问
- 1众开头的成语
- 2千锤百炼为一绿短文有什么道理
- 3一片关于描写夏季的雨的作文,要抒情散文,600—800字数
- 41伏等于多少毫安
- 5求一篇关于旅游的5人英语对话..大概6分钟的..希望单词别太深....急需啊..
- 6光和色素带中哪种色素的最窄,含量最少?我看很多图上显示胡萝卜素最少,
- 7上面一个“雨”下面一个“卡” 这个字念什么?
- 8关于中秋节的英语小短文,要有中文翻译.
- 9读了蜡烛这首诗,你联想到了什么人?为什么?请举例说明.
- 10黄土高原属于西北地区还是北方地区
- 11某数与它的一又二分之一相差八分之九,求这个数.(方程解)
- 12二十五元打八折怎么算
- 13英语原创新课堂六年级上册第27-30页答案
- 14一个米一个造是什么字?左边一个米字,右边一个造字.是什么字啊?
- 1525的x次方=2000,80的y次方=2000求 xy分之x+y 的值.(写出解题过程)



