实变函数证明题证明:所有系数为有理数的多项式可数还没学过笛卡尔集合,可数集的笛卡尔乘积是可数集,这个定理也没学过
 顶刮刮2022-10-04 11:39:541条回答
顶刮刮2022-10-04 11:39:541条回答
已提交,审核后显示!提交回复
共1条回复
 kelvin_ma 共回答了10个问题
kelvin_ma 共回答了10个问题 |采纳率80%- 不高于n次的有理系数多项式集合和有理数的n+1次笛卡尔集合存在一一对应.
即Pn={f(x)|f(x)=a0+a1x+...+anx^n,ai∈Q}~Q^(n+1)
可数集的笛卡尔乘积是可数集,所以Pn是可数集
而所有有理系数的多项式集合为Pn,n从0到无穷的并集
可数个可数集的并是可数集.
笛卡尔乘积就是,把几个集合分别任取一个元素作为坐标形成的集合.比如A*B={(a,b)|a∈A,b∈B}.至于那个定理,很基本的,看书上的证明. - 1年前
相关推荐
- 实变函数-元素(n1,n2,...,nk)是由k个正整数所组成,证明其全体成一可数集
 ffp0101011年前1
ffp0101011年前1 -
 那年那月那日那刻 共回答了16个问题
那年那月那日那刻 共回答了16个问题 |采纳率81.3%可数集就是可列集,只要可以将K个整数一一编号,即证明其为可数集.
显然,这是可以编号的(前提是你所说的正整数是无限个,而不是有限个)
或者也可以说,因为有理数集是可数集,一个可数集的任意子集至多是一个可数集.正整数集是有理数的子集,也至多是一个可数集.1年前查看全部
- 跪谢!实变函数:连续函数f(x)在(a,无穷)上广义积分收敛,f(x)是否在(a,无穷))Lebesgue 可积?
 a_ba1231年前1
a_ba1231年前1 -
 dingluwolf 共回答了12个问题
dingluwolf 共回答了12个问题 |采纳率91.7%不一定.Lebesgue可积是绝对可积.所以你随便取一个条件收敛的广义积分就是反例.1年前查看全部
- 实变函数达人,1.E 为自然数组成的数列的全体 ,证明,E 为不可数集 .2.证明 QxQ 的幂集 等价于 N 的幂集
实变函数达人,
1.E 为自然数组成的数列的全体 ,证明,E 为不可数集 .
2.证明 QxQ 的幂集 等价于 N 的幂集 N 为自然数集 . foaz1年前2
foaz1年前2 -
 静水起涟漪 共回答了27个问题
静水起涟漪 共回答了27个问题 |采纳率92.6%1.使用0-9的自然数,再用10(或是什么其它数)作小数点,易知这种数列可以表示一切实数,而这数列是E的子集.因为实数集不可数,所以E也不可数.
2.P(Q*Q)=P(N^4)=2^(card(N^4))=2^(card(N))=P(N),应该很简单.
P.S.card指cardinality,我不知道用中文怎么说.1年前查看全部
- 实变函数学十遍是真的?请问实变函数是一门什么样的科学?为什么这么难?大学的时候看哪一本实分析比较好呢?实变函数是不是对理
实变函数学十遍是真的?
请问实变函数是一门什么样的科学?为什么这么难?大学的时候看哪一本实分析比较好呢?实变函数是不是对理解微积分的原理很有好处? gh74h1年前1
gh74h1年前1 -
 marycay 共回答了13个问题
marycay 共回答了13个问题 |采纳率84.6%十遍函数学十遍,量子力学量力学,随机过程随机过...这都是顺口溜,没有任何依据.实变函数论和微积分都是属于分析这一分支.但是学实变函数,对于微积分并无多少帮助,因为它是微积分的后续课程.微积分所研究的,是可微,连...1年前查看全部
- 实变函数基础知识在看北大的“实变函数与泛函分析”有2个问题.1.书上有个定理说“有限个自然数构成的有序对的集合的全体是可
实变函数基础知识
在看北大的“实变函数与泛函分析”有2个问题.
1.书上有个定理说“有限个自然数构成的有序对的集合的全体是可列集”
如果无限个呢,是不是2^阿列夫0=c就是代表无限个自然数时候的反例?
2.还有证明无最大基数定理的时候,书上反证,假设f:2^A
然后构造了集合B={x∈A|x不∈f(x)},既然X属于A,怎么可能不属于A的幂集啊 serain1年前1
serain1年前1 -
 mazhaobing 共回答了18个问题
mazhaobing 共回答了18个问题 |采纳率94.4%1.不是对无限个都成立,有限个可以改成可列个定理仍然成立
2.f只是由A~2^A的映射,f的像为A的子集,未必包含x1年前查看全部
- 实变函数中可测集的集合类是什么?与开闭区间的区别和联系?
 涩男儿1年前1
涩男儿1年前1 -
 烟雨红颜bj 共回答了19个问题
烟雨红颜bj 共回答了19个问题 |采纳率84.2%可测集类是个西格玛代数,它的形成过程是这样的:先在基本空间x上定义一个测度函数m(是个集合函数且满足三条公理:非负性,空集零测性,可列可加性),然后像把这个测度函数的性质,尤其可列可加性“扩大”到让更多的集合满足,也就是做测度延拓,延拓的方法是定义x空间上的外测度m*,但是外测度并没有可列可加性(只有次可列可加性),这样还需要把外测度扩充后的能用外测度“测量”的所有集合再稍微缩小一点,找出这个集类中满足可列可加性的那些集合,Caratheodory经过多年研究后给出这样的条件(Cara条件,即”可拆分“条件,翻书),这样最终得到的集类定义成“可测集类”,并且可以证明这个集类是西格玛代数.因此可测集类是从原始集合类经过一次扩大和一次缩小后得到的集类,圆满解决了测度延拓问题.以上不仅对勒贝格测度定义适用,一般抽象测度例如概率测度,lebesgue-stieltijes测度等等也是同样的构造方法.
就勒贝格测度而言,基本空间是R^n,全体开集和闭集形成的代数就是Borel代数,其中的元素叫Borel集合.勒贝格可测集包含全部Borel集,亦即Borel代数是勒贝格可测集类的子集.开集和闭集是Borel集形成的基础.根据后续对勒贝格可测集的讨论,一个勒贝格可测集可以用一个开集从“外部”任意程度逼近,也可以用闭集从“内部”任意程度逼近,而且还可以拆成一个Borel集和一个勒贝格零测集的并或者差.
希望我的回答能帮助你.1年前查看全部
- 实变函数证明题求助!Show that if A has finite measure and ε>0,then A i
实变函数证明题求助!
Show that if A has finite measure and ε>0,then A is the disjoint union of a finite number of measurable sets,each of which has measure at nost ε.
翻译:证明:如果A有有限测度,ε>0,那么A是有有限个不相交的可测集的并,每一个可测集有最大测度ε bell1851年前1
bell1851年前1 -
 FTSAH 共回答了19个问题
FTSAH 共回答了19个问题 |采纳率94.7%我不知道你用的那个版本,测度背景等我不清楚,我以一维勒贝格测度为例证明:
因为A有有限测度,由测度定义知道,对任意ε>0,存在a,b,满足m(A-[a,b])1年前查看全部
- 实变函数问题中的有界变差函数问题
实变函数问题中的有界变差函数问题
有界变差函数至多有可数个不连续点,不可导点构成零测度集。这句话正确吗?
关于[a,b]上的绝对连续函数F(x)及其导数,下列说法正确吗?
在[a,b]上几乎处处有导数的有界函数F(x)不一定连续,但F(x)本身一定可积。而它的导函数F'(x)就不一定可积了。即使可积也不一定满足牛氏公式。 a78265711年前1
a78265711年前1 -
 winbilly 共回答了18个问题
winbilly 共回答了18个问题 |采纳率88.9%这句话说法正确1年前查看全部
- 复变函数与实变函数的区别和联系?
复变函数与实变函数的区别和联系?
最近《数学物理方法》老师要我们写一篇论文, scarwxz1年前1
scarwxz1年前1 -
 kiki1218 共回答了25个问题
kiki1218 共回答了25个问题 |采纳率88%复变和实变,自变量的范围不同,复变函数研究对相是解析函数,讨论复数之间的依存关系,而实变函数研究范围较广,复变函数只是前者在微积分领域的推广与发展,亦称复分析.1年前查看全部
- 实变函数是什么?总是听说实变函数学十遍,实变函数主要学的是什么东西?为什么实变函数这么难?实变函数不是对数学分析的理论补
实变函数是什么?
总是听说实变函数学十遍,实变函数主要学的是什么东西?为什么实变函数这么难?实变函数不是对数学分析的理论补充吗?如果是的话,实变函数需要的知识都有哪些? 校帅1年前2
校帅1年前2 -
 谁比谁累 共回答了14个问题
谁比谁累 共回答了14个问题 |采纳率100%实变函数的主要内容是lebsegue测度与积分理论,是一种与传统黎曼积分不同的体系下的积分.其中测度与概率论有很大的联系.
只要有数学分析的基础就可以学实变函数.
实变难是难在它的理论体系,只要从本质上思考接受它,再配上典型的习题,学起来也不会太困难.1年前查看全部
- 实变函数、泛函分析是讲什么的?具体特点是什么?
 coolsmilehigh1年前2
coolsmilehigh1年前2 -
 qhenqian 共回答了15个问题
qhenqian 共回答了15个问题 |采纳率100%实变函数的内容
以实数作为自变量的函数就做实变函数,以实变函数作为研究对象的数学分支就叫做实变函数论.它是微积分学的进一步发展,它的基础是点集论.什么是点集论呢?点集论是专门研究点所成的集合的性质的理论.也可以说实变函数论是在点集论的基础上研究分析数学中的一些最基本的概念和性质的.比如,点集函数、序列、极限、连续性、可微性、积分等.实变函数论还要研究实变函数的分类问题、结构问题.
实变函数论的内容包括实值函数的连续性质、微分理论、积分理论和测度论等.这里我们只对它的一些重要的基本概念作简要的介绍.
实变函数论的积分理论研究各种积分的推广方法和它们的运算规则.由于积分归根到底是数的运算,所以在进行积分的时候,必须给各种点集以一个数量的概念,这个概念叫做测度.
什么实测度呢?简单地说,一条线段的长度就是它的测度.测度的概念对于实变函数论十分重要.集合的测度这个概念实由法国数学家勒贝格提出来的.
为了推广积分概念,1893年,约当在他所写的《分析教程》中,提出了“约当容度”的概念并用来讨论积分.1898年,法国数学家波莱尔把容度的概念作了改进,并把它叫做测度.波莱尔的学生勒贝格后来发表《积分、长度、面积》的论文,提出了“勒贝格测度”、“勒贝格积分”的概念.勒贝格还在他的论文《积分和圆函数的研究》中,证明了有界函数黎曼可积的充分必要条件是不连续点构成一个零测度集,这就完全解决了黎曼可积性的问题.
勒贝格积分可以推广到无界函数的情形,这个时候所得积分是绝对收敛的,后来由推广到积分可以不是绝对收敛的.从这些就可以看出,勒贝格积分比起由柯西给出后来又由黎曼发扬的老积分定义广大多了.也可以看出,实变函数论所研究的是更为广泛的函数类.
自从维尔斯特拉斯证明连续函数必定可以表示成一致收敛的多项式级数,人们就认清连续函数必定可以解析地表达出来,连续函数也必定可以用多项式来逼近.这样,在实变函数论的领域里又出现了逼近论的理论.
什么是逼近理论呢?举例来说,如果能把 A类函数表示成 B类函数的极限,就说 A类函数能以 B类函数来逼近.如果已经掌握了 B类函数的某些性质,那么往往可以由此推出 A类函数的相应性质.逼近论就是研究那一类函数可以用另一类函数来逼近、逼近的方法、逼近的程度和在逼近中出现的各种情况.
和逼近理论密切相关的有正交级数理论,三角级数就是一种正交级数.和逼近理论相关的还有一种理论,就是从某一类已知函数出发构造出新的函数类型的理论,这种理论叫做函数构造论.
总之,实变函数论和古典数学分析不同,它是一种比较高深精细的理论,是数学的一个重要分支,它的应用广泛,它在数学各个分支的应用是现代数学的特征.
实变函数论不仅应用广泛,是某些数学分支的基本工具,而且它的观念和方法以及它在各个数学分支的应用,对形成近代数学的一般拓扑学和泛涵分析两个重要分支有着极为重要的影响.
泛函分析的产生
十九世纪以来,数学的发展进入了一个新的阶段.这就是,由于对欧几里得第五公设的研究,引出了非欧几何这门新的学科;对于代数方程求解的一般思考,最后建立并发展了群论;对数学分析的研究又建立了集合论.这些新的理论都为用统一的观点把古典分析的基本概念和方法一般化准备了条件.
本世纪初,瑞典数学家弗列特荷姆和法国数学家阿达玛发表的著作中,出现了把分析学一般化的萌芽.随后,希尔伯特和海令哲来创了“希尔伯特空间”的研究.到了二十年代,在数学界已经逐渐形成了一般分析学,也就是泛函分析的基本概念.
由于分析学中许多新部门的形成,揭示出分析、代数、集合的许多概念和方法常常存在相似的地方.比如,代数方程求根和微分方程求解都可以应用逐次逼近法,并且解的存在和唯一性条件也极其相似.这种相似在积分方程论中表现得就更为突出了.泛函分析的产生正是和这种情况有关,有些乍看起来很不相干的东西,都存在着类似的地方.因此它启发人们从这些类似的东西中探寻一般的真正属于本质的东西.
非欧几何的确立拓广了人们对空间的认知,n维空间几何的产生允许我们把多变函数用几何学的语言解释成多维空间的影响.这样,就显示出了分析和几何之间的相似的地方,同时存在着把分析几何化的一种可能性.这种可能性要求把几何概念进一步推广,以至最后把欧氏空间扩充成无穷维数的空间.
这时候,函数概念被赋予了更为一般的意义,古典分析中的函数概念是指两个数集之间所建立的一种对应关系.现代数学的发展却是要求建立两个任意集合之间的某种对应关系.
这里我们先介绍一下算子的概念.算子也叫算符,在数学上,把无限维空间到无限维空间的变换叫做算子.
研究无限维线性空间上的泛函数和算子理论,就产生了一门新的分析数学,叫做泛函分析.在二十世纪三十年代,泛函分析就已经成为数学中一门独立的学科了.
泛函分析的特点和内容
泛函分析的特点是它不但把古典分析的基本概念和方法一般化了,而且还把这些概念和方法几何化了.比如,不同类型的函数可以看作是“函数空间”的点或矢量,这样最后得到了“抽象空间”这个一般的概念.它既包含了以前讨论过的几何对象,也包括了不同的函数空间.
泛函分析对于研究现代物理学是一个有力的工具.n维空间可以用来描述具有n个自由度的力学系统的运动,实际上需要有新的数学工具来描述具有无穷多自由度的力学系统.比如梁的震动问题就是无穷多自由度力学系统的例子.一般来说,从质点力学过渡到连续介质力学,就要由有穷自由度系统过渡到无穷自由度系统.现代物理学中的量子场理论就属于无穷自由度系统.
正如研究有穷自由度系统要求 n维空间的几何学和微积分学作为工具一样,研究无穷自由度的系统需要无穷维空间的几何学和分析学,这正是泛函分析的基本内容.因袭,泛函分析也可以通俗的叫做无穷维空间的几何学和微积分学.古典分析中的基本方法,也就是用线性的对象去逼近非线性的对象,完全可以运用到泛函分析这门学科中.
泛函分析是分析数学中最“年轻”的分支,它是古典分析观点的推广,它综合函数论、几何和代数的观点研究无穷维向量空间上的函数、算子、和极限理论.他在二十世纪四十到五十年代就已经成为一门理论完备、内容丰富的数学学科了.
半个多世纪来,泛函分析一方面以其他众多学科所提供的素材来提取自己研究的对象,和某些研究手段,并形成了自己的许多重要分支,例如算子谱理论、巴拿赫代数、拓扑线性空间理论、广义函数论等等;另一方面,它也强有力地推动着其他不少分析学科的发展.它在微分方程、概率论、函数论、连续介质力学、量子物理、计算数学、控制论、最优化理论等学科中都有重要的应用,还是建立群上调和分析理论的基本工具,也是研究无限个自由度物理系统的重要而自然的工具之一.今天,它的观点和方法已经渗入到不少工程技术性的学科之中,已成为近代分析的基础之一.
泛函分析在数学物理方程、概率论、计算数学、连续介质力学、量子物理学等学科有着广泛的应用.近十几年来,泛函分析在工程技术方面有获得更为有效的应用.它还渗透到数学内部的各个分支中去,起着重要的作用.1年前查看全部
- 如何将二元实变函数转化为复变函数
如何将二元实变函数转化为复变函数
知道了u=(x,y) v=(x,y) 如何转化成f(z)的形式 urilla1年前1
urilla1年前1 -
 东南向南 共回答了17个问题
东南向南 共回答了17个问题 |采纳率100%原来u,v是f(z)的实部和虚部(这个在题目处最好说明一下,不然会误解).
f(z)=u+iv=(2xy-2y)+i(2x-x^2+y^2+c)
=2(x-1)y+i(y^2-(x-1)^2+c+1)
=i{y^2-2i(x-1)y+[i(x-1)]^2+c+1}
=i{[y-i(x-1)]^2+c+1}
=i{[-i(iy+x-1)]^2+c+1}
=i{(-i)^2(z-1)^2+c+1}
=-i(z-1)^2+i(c+1)1年前查看全部
- 实变函数的主要意义
 叶鑫1年前2
叶鑫1年前2 -
 hby-ice 共回答了20个问题
hby-ice 共回答了20个问题 |采纳率95%在微积分学中,主要是从连续性、可微性、黎曼可积性三个方面来讨论函数(包括函数序列的极限函数).如果说微积分学所讨论的函数都是性质“良好”的函数(例如往往假设函数连续或只有有限个间断点),那么,实变函数论是从连续性、可微性、可积性三个方面讨论最一般的函数,包括从微积分学来看性质“不好”的函数.它所得到的有关的结论自然也适用于性质“良好”的函数.实变函数论是微积分学的发展和深入.函数可积性的讨论是实变函数论中最主要的内容.它包括H.L.勒贝格的测度、可测集、可测函数和积分以及少许更一般的勒贝格-斯蒂尔杰斯测度和积分的理论(见勒贝格积分).这种积分比黎曼积分是更为普遍适用和更为有效的工具,例如微积分基本定理以及积分与极限变换次序.1年前查看全部
- 实变函数中开集都是可测的吗
 善蚌寺的堪布1年前1
善蚌寺的堪布1年前1 -
 mishen 共回答了17个问题
mishen 共回答了17个问题 |采纳率82.4%如果你说的是直线上的开集,那么答案是都可测,因为所有的开集只有两种结构——由有限个开区间做交运算得到,或由任意多个开区间做并运算得到——开区间全部都是可测的,所以由测度公理可以推出所有的开集均可测.1年前查看全部
- 自变量是实数,因变量是复数的函数是实变函数?
 cxdcxd20061年前2
cxdcxd20061年前2 -
 战争与重逢 共回答了17个问题
战争与重逢 共回答了17个问题 |采纳率94.1%是,变指自变量.1年前查看全部
- 实变函数上下限集和上下确界的问题
实变函数上下限集和上下确界的问题
说错了,实变函数的下限集等于n大于m的无穷集的交为什么还要并一下,交了不是就没有并了吗?还有上下确界,比如上确界,都已经上确了,再又一个下确界不是化蛇添足了吗? zjf_fly20011年前1
zjf_fly20011年前1 -
 娃哈哈nj327 共回答了14个问题
娃哈哈nj327 共回答了14个问题 |采纳率85.7%就以下限集为例,有的概念不是一步就能引出的,我们先定义递增集合列的极限集,如果集合列An是递增的(即A1包含于A2包含于A3...包含于An...),那么定义它们的并为其极限集.对于一般的集合列An,不一定有单调性,为了定义类似的集合,我们可以通过这些集构造出一个递增的集合列,构造的方法就是把An中第n个以后所有的集合取交集,构成一新集合列Bn=∩Ak(k从n取到∞),这样Bn是递增的(因为随着n的增大,前面不参与交运算的集合就越来越多,其中一些很”小“的集合就会在交运算中失去作用了).对Bn这个递增的集合列,再按开始的定义求其极限集,也就是∪Bn(n从1取到∞),把这个极限集就定义为An的下限集,即An的下限集=∪∩Ak(k从n取到∞,n从1取到∞)1年前查看全部
- 跪谢!实变函数:连续函数f(x)在(a,无穷)上广义积分收敛,f(x)是否在(a,无穷))Lebesgue 可积?
跪谢!实变函数:连续函数f(x)在(a,无穷)上广义积分收敛,f(x)是否在(a,无穷))Lebesgue 可积?
求详细解释!跪谢 郑州票务1年前1
郑州票务1年前1 -
 jessie8203 共回答了16个问题
jessie8203 共回答了16个问题 |采纳率87.5%不一定.Lebesgue可积是绝对可积.所以你随便取一个条件收敛的广义积分就是反例.1年前查看全部
- 汉译英,在数学分析,复变函数和实变函数等课程中,收敛和极限是常见的两个概念.这两个概念又可以细分为不同意义下的极限和收敛
汉译英,
在数学分析,复变函数和实变函数等课程中,收敛和极限是常见的两个概念.这两个概念又可以细分为不同意义下的极限和收敛,并且附带着诸如连续性等性质的改变.收敛与极限理论贯穿整个数学分析、实变函数和复变函数之中,是数学中的重要内容和难点.认识收敛和极限的思想是把握和理解它们之间理论的前提.极限是分析数学中最基本和最重要的概念,特别是数学分析中,其思想贯穿整个数学分析的始终,并且,在数学的其他领域中也有着重要作用.极限定义的基础是点与点之间距离.由于在不同空间中距离(或相当于距离)给出的方式和含义上的差别而导致出不同的收敛. 一流星_xx1年前4
一流星_xx1年前4 -
 neusj 共回答了29个问题
neusj 共回答了29个问题 |采纳率93.1%n the mathematical analysis,complex-variable function and realvariable funktion courses,convergence and limit the two concepts is common.These two concepts and can be divided into different limit and convergence,and with such properties such as the continuity of the change.Convergence and limit theory throughout the mathematical analysis,realvariable funktion and complex-variable function,which is the important content and the difficulties in mathematics.Knowledge of the thoughts and convergence and understanding between them is the premise of theory.Limit is the most basic mathematical analysis and the most important concept,especially the mathematical analysis,its thought throughout the mathematical analysis,and other fields of mathematics,in also plays an important role.The foundation is the ultimate definition and distance between the point.Due to the different space distance (or equivalent) distance and the difference in meaning and leads to a different convergence.1年前查看全部
- 实变函数中,勒贝格控制收敛定理,列维定理与Fatou引理之间的关系
 xxxxxxx7111年前1
xxxxxxx7111年前1 -
 464657yt 共回答了23个问题
464657yt 共回答了23个问题 |采纳率91.3%简而言之,Fatou引理导出勒贝格控制收敛定理,勒贝格控制收敛定理导出列维定理1年前查看全部
- 实变函数:证明[a,b]上定义的连续函数的全体势为c
 悲情的荆棘鸟1年前0
悲情的荆棘鸟1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 实变函数:f是可测集E上定义的函数,则f在E上可测的充要条件是fχE在R上可测,给个思路就行
实变函数:f是可测集E上定义的函数,则f在E上可测的充要条件是fχE在R上可测,给个思路就行
给个思路就行 西柯1年前1
西柯1年前1 -
 qlnsyho 共回答了18个问题
qlnsyho 共回答了18个问题 |采纳率83.3%χE 应该是 E的示性函数,定义如下:如果 x属于E,χE(x)=1,如果 x不属于E,χE(x)=0.于是:如果 x属于E,fχE(x)=f(x),如果 x不属于E,fχE(x)=0.直接根据可测的定义验证就好啦.===> 如果fχE在R上可测,任给 R 中可...1年前查看全部
- 一道实变函数或者叫数学分析的证明题
一道实变函数或者叫数学分析的证明题
证明任何闭集都可表成可数多个开集的交 nanarain1年前1
nanarain1年前1 -
 小荷花吃瓜 共回答了21个问题
小荷花吃瓜 共回答了21个问题 |采纳率100%闭集A是R的子集.
A必有可数稠密子集{xn}.(用无限加细的区间分割即可取出一列.事实上连R都有可数稠密子集Q.)令dn=inf{r:(xn-r,xn+r)是A的子集},于是:
无穷 无穷
A = 交 并 (xn-dn-1/k,(xn+dn+1/k) (注意:开集可列并仍为开集)
k=1 n=1
于是A可表为可数多个开集的交1年前查看全部
- 这个问题是有关实变函数的问题,外测度究竟是一个实数,还是一个点(x1,x2,.xn),希望懂的不吝赐教,
 hhdong1181年前3
hhdong1181年前3 -
 专业FFFF 共回答了20个问题
专业FFFF 共回答了20个问题 |采纳率90%由外测度的定义可知外测度是一列数的下确界,显然是实数啊.其实外侧度只是为了以后学习中的测度做铺垫,若外测度满足卡氏条件,则此时外测度就是测度,具体简单来说,测度在一维空间中就是我们说的长度,在二维空间中就是我们说的面积,在三维空间中就是所谓的体积,在高维空间中也就是抽象的“体积”1年前查看全部
- 实变函数:一个集合包含于另一个集合,前一个可测且前一个的测度等于后一个的外侧度,证明后一个集合可测
 黄孩儿1年前1
黄孩儿1年前1 -
 shiyuxing 共回答了15个问题
shiyuxing 共回答了15个问题 |采纳率86.7%只要证明B集合的内外测度相等.
B集合的外测度等于A的外侧度,又因为A包含于B,所以B的内测度>=A的内测度.而B的内测度1年前查看全部
- 实变函数刚开始学习,集合的问题如图,为什么上面只能是属于,下面是等于,这两个有什么区别呢?最好有证明过程。根据定义第二个
实变函数刚开始学习,集合的问题
如图,为什么上面只能是属于,下面是等于,这两个有什么区别呢?
最好有证明过程。根据定义第二个不是一一对应的。
你看一下定义
http://wenku.baidu.com/view/0e696ddc5022aaea998f0fdc.html
在13页。
如果简单,请把过程写一下,我想知道证明过程中到底哪里不一样。
反例我也会举得出来,但证明过程不好把握。
谢谢!
我写一下我的证明,证明第一个式子左边到右边。
记左边的为P,右边的为Q
y属于P,即存在x属于A1,A2……的交,使得y=f(x)
即对任意的alpha,成立x属于A_alpha,使得y=f(x)
于是对任意的alpha,y属于f(A_alpha)
于是y属于Q
但问题是我觉得对以上证明,每一步都可以反过去。
好像感觉是从 y属于f(A_alpha) 不能推出 成立x属于A_alpha,使得y=f(x)

 萧刃11111年前2
萧刃11111年前2 -
 bengezhao 共回答了14个问题
bengezhao 共回答了14个问题 |采纳率78.6%第一个式子是"包含于",原因是:
那些A可以交成一个很小的集合,甚至是空集,
但并不影响他们每个A的像可以交成较大的集合.
换句话说,
在某个A中但不在这些A的交中的那些元素的像可以是相同的.
第二个式子则是说那些B的交的原像,是并且只是这样的元素构成的,
它被映射到所有的B的交中,也就是说它在每个B的原像中.
这两个结论都是直观的,证明也是平凡的.
看了你的补充,现在说一下反过来哪里有问题。
对任意的y属于Q,有:对任意的alpha,y属于f(A_alpha)。
即
对任意的alpha,存在x_alpha属于A_alpha,使得f(x_alpha)=y。
注意说的是存在x_alpha,也就是说,这个x与前面的alpha有关。
也就意味着,不同的A_alpha中可能有不同的x_alpha使得f(x_alpha)=y。
因此可能没有公共的x,它属于每个A_alpha,并且满足f(x)=y。
这么解释可以吗?1年前查看全部
- 实变函数,复变函数,近世代数这三门课的内容是什么?哪一门课比较难理解?
 黑夜的孤独者1年前1
黑夜的孤独者1年前1 -
 沂水濯缨 共回答了14个问题
沂水濯缨 共回答了14个问题 |采纳率85.7%实变函数,顾名思义,是实函数,但不是常规的实函数,是广义的实函数,更多研究的是“突变”类型的实函数,比如,我们在数学分析中主要谈论的还是连续函数可微函数,对于很不连续的函数便不再研究,比如狄利克雷函数黎曼函数等等,但实变函数便研究这种函数,求这种函数的积分等等
复变函数,顾名思义,是复函数,是将数学分析中的函数扩展到复函数,研究这些函数的解析性质
近世代数是代数学的一个分支,研究近代以来的代数学,主要是群环域理论,这是三个很重要的代数系统
实变是公认比较难的1年前查看全部
- 实变函数的测度问题.请问实变函数论中,测度m(A-B)>或=mA+mB,这个关系式是怎么来的?还有如果设A,B为可测集,
实变函数的测度问题.
请问实变函数论中,测度m(A-B)>或=mA+mB,这个关系式是怎么来的?
还有如果设A,B为可测集,mB=0,则m(A-B)和mA之间的关系是什么?大于还是等于,还是小于,说出理由.
本人困惑了很久, linyn05921年前2
linyn05921年前2 -
 shen7333219 共回答了22个问题
shen7333219 共回答了22个问题 |采纳率90.9%m(A-B)>或=mA+mB 应该是m(A-B)>或=mA-mB
测度实际上是集合到【0,R)的一个映射,它必须满足通常的长度的基本关系.m(A-B)>或=mA-mB
这个是测度的次可加性,满足可加性的测度(如果还同时满足其他性质的话)是找不到的,只能退而求其次要求它满足次可加性.
mA》=m(A-B)》=mA+mB=mA 所以是等于.
另外mA》=m(A-B)是测度的单调性.1年前查看全部
- 实变函数中的集合的距离问题`两集合F1,F2不相交,能否推出它们之间的距离d(F1,F2)=infd(P,Q)>0?其中
实变函数中的集合的距离问题`
两集合F1,F2不相交,能否推出它们之间的距离
d(F1,F2)=infd(P,Q)>0?其中P属于F1,Q属于F2.请说明理由,给出详细的证明.
若F1,F2都是闭集呢?你的回答错了!F1=(0,1),F2=(1,2),两集合不相交,距离还是大于零。
你的证明不对啊!我可以举出反例啊!F1={Xn;Xn=n-1/n},F2={Yn;Yn=n+1/n},n是自然数,则F1,F2都是闭集,F1,F2不相交,但
d(F1,F2)=inf{1/2n}=0,n是自然数。
你所说的“由于F1,F2是闭集,那么Ak->A属于F1,Bk->B属于F2”不对啊! 吊儿郎当小阿哥1年前1
吊儿郎当小阿哥1年前1 -
 啥咪 共回答了15个问题
啥咪 共回答了15个问题 |采纳率93.3%不能.反例,F1=(0,1),F2=(1,2),两集合不相交,但是距离为零 -------------------------------期望你能复习一下inf的意义.对了,如果是两个都是闭集得话就对了.证明:反证如果d(F1,F2)=0,那么存在两数列Ak属于F1,Bk属...1年前查看全部
- 实变函数 依测度收敛设{fn}在区间[a,b]依测度收敛于f g(x)在R上一直连续 证明{g(fn)}在[a,b]依测
实变函数 依测度收敛
设{fn}在区间[a,b]依测度收敛于f g(x)在R上一直连续
证明{g(fn)}在[a,b]依测度收敛于{g(f)} 卖棺材的女人1年前2
卖棺材的女人1年前2 -
 jlhg2040 共回答了14个问题
jlhg2040 共回答了14个问题 |采纳率100%因为{fn}在区间[a,b]依测度收敛于f ,{fn}的子列{fni}依测度收敛于f.由黎斯定理,存在子列{fni},使得i趋近无穷大时lim{fni}=f,几乎处处于[a,b].
由g(x)在R上一致连续,得i趋近无穷大时lim g(fni)=g(f),几乎处处于[a,b].
在区间[a,b]上,由可测集上的连续函数是可测函数,得知g(fni)是可测函数且g(fni)是有限的.
再由Lebesgue定理:直接得到g(fni)依测度收敛于g(f)1年前查看全部
- 实变函数中看到的,比如ξ→0(趋近于0),箭头上有字母p或希腊字母μ,
 sh_fei1年前1
sh_fei1年前1 -
 yezizhu1123 共回答了24个问题
yezizhu1123 共回答了24个问题 |采纳率91.7%依概率收敛,依测度收敛1年前查看全部
- 实变函数求助证明图中等式成立,是在通过积分和的方式下来定义L-积分时的情况下那个,“根据Lebesgue积分的定义”,这
实变函数求助
证明图中等式成立,是在通过积分和的方式下来定义L-积分时的情况下那个,“根据Lebesgue积分的定义”,这里的定义是哪种定义?简单函数逼近方式还是积分和方式?

 tope1年前1
tope1年前1 -
 SPICE666 共回答了18个问题
SPICE666 共回答了18个问题 |采纳率94.4%只需要证明n=2的情况,再根据归纳法可得.
n=2时,根据Lebesgue积分的定义,当振幅delta足够小时
左边=c1*m(E1E2)+c2*m(E2E1)+(c1+c2)*m(E1∩E2)
=c1*(m(E1E2)+m(E1∩E2))+c2*(m(E2E1)+m(E1∩E2))
=c1*m(E1)+c2*m(E2)=右边
后者1年前查看全部
- 一道周民强老师课本上的实变函数的题目
 aenty1231年前1
aenty1231年前1 -
 Mr_Baily 共回答了14个问题
Mr_Baily 共回答了14个问题 |采纳率92.9%记e=q/2,令 Fn={x | f(x)=m时,其测度q-e=q/2,显然 f在E上的积分 > f在EFm上的积分 > q/m.1年前查看全部
- 实变函数中孤立点的定义?能不能举例子说明?
 钱没处花爱来找碴1年前1
钱没处花爱来找碴1年前1 -
 ldb0509 共回答了10个问题
ldb0509 共回答了10个问题 |采纳率90%比如(1,2)∪{3},其中3就是孤立点,孤立点(孤立点必须属于原集合)其实就是以该点为中心做个任意小的邻域,如果该邻域内除了该点外,与原集合交集为空集的话,则该点为孤立点.1年前查看全部
- 复变函数和实变函数的联系是什么?为什么要研究复变函数呢?
 xiaoyaoyou20071年前1
xiaoyaoyou20071年前1 -
 cyclone19 共回答了21个问题
cyclone19 共回答了21个问题 |采纳率90.5%实变函数和复变函数都是研究函数的数学性质的,虽然只是定义域不同,但两门课的内容大相径庭,实变函数可以看做是数学分析的后继课程,主要是分析(勒贝格积分理论)的内容,而复变函数的研究手段和课程内容对数学三大分支:分析(柯西积分理论),几何(黎曼面理论),代数(魏尔斯特拉斯级数理论)都有涉及,且都占有很重要的位置.个人学习感觉是,解决复变函数的问题的方法很灵活,而实变函数的内容很有挑战性,很考验推理的严谨性(有许多和直观不附的现象)与数学构造能力.
我个人认为要回答为什么要干某事有时是一件不容易的事,不同的人干一件事也有不同的理由.有的人可能会觉得复变函数理论很有美感当作艺术去欣赏(大多数纯数学家),也有的人发觉复变函数理论与数学许多分支联系密切希望借助它更进一步理解数学分支之间的联系(数学史学家和一些纯数学家),还有的人发现复数运算有很多很好的性质(如表示旋转)可以在某些偏理论的实际问题中得到应用(好像复数及复变函数在电子电工领域有很广的应用,不大清楚),这些人是应用数学家和工程师.
就像是很难说为什么要去研究哥德巴赫猜想一样,看起来“不管大于等于6的偶数是否都能表示成两个素数的和”与我们的生活一点关系也没有,但是在试图解决它的同时发展了许许多多数论的新方法,更令人惊奇的是,作为最纯数学的“数论”竟能应用到导弹控制发射(华罗庚先生和王元先生做的研究工作).1年前查看全部
- 复变函数为什么在解析点处的各阶导数也解析,实变函数却不行,求导在图像上到底代表什么意思
 highwayok1年前2
highwayok1年前2 -
 zorro2393406 共回答了24个问题
zorro2393406 共回答了24个问题 |采纳率87.5%这个问题问的好啊!去年我在学复分析的时候也考虑过.我觉得关键在于复变函数的可导与实函数不一样.虽然都是函数值的变化比上自变量的变化的极限,但是一个是实数相除,而另一个是复数相除.而且如果把复变函数看成是R2到R2的映射的话,复变函数可导条件把复函数的实部和虚部联系在了一起(柯西黎曼条件),而如果在实函数可导意义下,仅是实部和虚部分别可导,它们之间推不出任何关系.可见复可导比实可导条件强.至于复函数的导数(对于固定点它是个复数)的几何意义,可以看成是过那一点的某条曲线与经过这个复函数映射下的曲线的单位切向量的夹角与长度的改变1年前查看全部
- 求助实变函数中riemann可积的问题
求助实变函数中riemann可积的问题
1 若E为[a,b]上测度为零的子集合,其特征函数在[a,b]上是否R-可积?
2 若E为[a,b]上的疏朗集,其特征函数在[a,b]上是否R-可积?
3 若E为[a,b]上测度为零的疏朗集,其特征函数在[a,b]上是否R-可积?
4 若E为[a,b]上测度为零的闭集,其特征函数在[a,b]上是否R-可积? 坐看云起19791年前2
坐看云起19791年前2 -
 wsdtc1999 共回答了14个问题
wsdtc1999 共回答了14个问题 |采纳率92.9%有界区域内有界函数PIEMANN可积等价于不连续点集0测.
1不一定 [a,b]中有理数的特征函数 所有点处不连续.
2,3什么是 疏朗集?
4 R-可积 不连续点为此闭集中的点 0测1年前查看全部
- 实变函数中的Lebesgue点集与可微点集是否有包含关系?我感觉Lebesgue点集包含可微点集,
实变函数中的Lebesgue点集与可微点集是否有包含关系?我感觉Lebesgue点集包含可微点集,
说反了,我感觉是Lebesgue点集包含于可微点集 GLD3211年前1
GLD3211年前1 -
 小刀4522 共回答了25个问题
小刀4522 共回答了25个问题 |采纳率84%Dirichlet函数在[0,1]上是Lebesgue可积的,从而在[0,1]上几乎处处是Lebesgue点.然而不可微.
注,有定理:若f ∈ L([a,b]),则对[a,b]中几乎处处的点x,都有
lim_{h rightarrow 0} (1/h) int_0^h |f(x+t) - f(x)| dt = 0.
即在[a,b]几乎处处是Lebesgue点.1年前查看全部
- 复变函数的导数实变函数中只要知道一个函数的解析式,就可以不用导数定义而只靠导数公式就可以求得导数.那么复变函数中是不是也
复变函数的导数
实变函数中只要知道一个函数的解析式,就可以不用导数定义而只靠导数公式就可以求得导数.那么复变函数中是不是也只要知道一个函数的解析式,就可以不用导数定义而只靠导数公式就可以求得导数?
不是复合函数 yoyochan19871年前3
yoyochan19871年前3 -
 紫鲱鸟 共回答了13个问题
紫鲱鸟 共回答了13个问题 |采纳率84.6%把函数分成实部和复部分别求导就行了
EG:y=2x+i(3x)
y'=2+i(3)1年前查看全部
- 实变函数 函数F和F的绝对值的可测和可积的关系
实变函数 函数F和F的绝对值的可测和可积的关系
RT wanglai8101年前1
wanglai8101年前1 -
 moving_xm 共回答了16个问题
moving_xm 共回答了16个问题 |采纳率100%若F(x) Lebesgue可测则|F(x)|也Lebesgue可测,用定义直接证明.但是反过来不行,比如F在某不可测集上取1,余下取-1.
F(x) Lebesgue可积等价于|F(x)| Lebesgue可积,直接用定义验证.1年前查看全部
- 实变函数问题f是勒贝格可积的且一致连续,证明当x趋向于无穷时,f(x)的极限是否存在,若存在,证明其是否一定为零
 ff52号1年前1
ff52号1年前1 -
 PKCHEN68 共回答了16个问题
PKCHEN68 共回答了16个问题 |采纳率75%是,并且是零.
可以假定f>=0,否则以|f| 代替f,仍然Lebesgue可积,并且一致连续.如果能证明 |f| 的极限是0,那么自然推出f的极限是0.
现在f>=0.对于给定的h>0,要找一个A,使得当x>A的时候,f(x)1年前查看全部
- 实变函数 设f1,f2是rn中闭集,且f1∩f2=空集,试证明存在开集G1,G2,使得G1∩G2=空集且有G1包含F1,
实变函数 设f1,f2是rn中闭集,且f1∩f2=空集,试证明存在开集G1,G2,使得G1∩G2=空集且有G1包含F1,G2包含F2
 咔叽龙卷风1年前1
咔叽龙卷风1年前1 -
 竹林斜影 共回答了14个问题
竹林斜影 共回答了14个问题 |采纳率85.7%王丽丽呀!1年前查看全部
- 二元实变函数导数的几何意义是什么
二元实变函数导数的几何意义是什么
一元实变函数的导数几何意义是该点斜率,那二元实变函数的导数的几何意义是什么呢? EMINENS1年前2
EMINENS1年前2 -
 lyx53115 共回答了17个问题
lyx53115 共回答了17个问题 |采纳率100%为探索二元函数z=f(x,y)方向导数的几何特征,使用代数分析和矢量分析的方法研究函数z=f(x,y)的方向导数.对于由方程z=f(x,y)给出的曲面S上的曲线C:z=f(x,y)且y=y0+tanα.(x-x0),设L是过曲面S上(x0,y0,f(x0,y0))点曲线C的切线,θ是有向直线L与矢量AB→的夹角.那么二元函数z=f(x,y)在(x0,y0,f(x0,y0))点沿方向AB→的方向导数就是tanθ.1年前查看全部
- 对实变函数中鲁津定理的理解实变函数中的鲁津定理表达的是“可测函数都是基本上连续的函数”,但分段函数也是可测函数,我咋怎么
对实变函数中鲁津定理的理解
实变函数中的鲁津定理表达的是“可测函数都是基本上连续的函数”,但分段函数也是可测函数,我咋怎么看它也不像“基本上连续”的函数呢?它明明有间断点的呀,还是我对连续的定义理解的有偏差? 梦中蝴蝶家万里1年前2
梦中蝴蝶家万里1年前2 -
 wellgo1 共回答了11个问题
wellgo1 共回答了11个问题 |采纳率100%什么叫"基本上连续"?
在这里,"基本上连续"的数学意义是:可测函数在其定义域上去掉一个测度任意小的集合后连续
分段函数是有间断点,但其间断点的集合的测度是任意小,所以是"基本上连续"1年前查看全部
- f(x)是定义于E上的实函数中的E是代表什么实变函数里面的
 浮云1981年前2
浮云1981年前2 -
 phoenixtigerdog 共回答了27个问题
phoenixtigerdog 共回答了27个问题 |采纳率85.2%可测集!也是一个集合1年前查看全部
- 鲁丁的实分析与复分析就是实变函数与复变函数吗
 evom1年前1
evom1年前1 -
 cotine1 共回答了22个问题
cotine1 共回答了22个问题 |采纳率81.8%是的1年前查看全部
- 复变函数 x的平方+y的平方 只在z=0可导吗 实变函数是不是处处可导了
 依然洋溢1年前0
依然洋溢1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 求证明,是一道实变函数题,但是是证明积分的极限等于0
求证明,是一道实变函数题,但是是证明积分的极限等于0
证明这个式子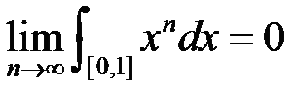 ,是出现在实变函数课本中非负可测函数积分那一节的课后题.
,是出现在实变函数课本中非负可测函数积分那一节的课后题.  晨媚21年前0
晨媚21年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 实变函数里刚讲到勒贝格积分时,提到一个特征函数,f(x)=求和(ci*Xei(x))那个Xei(x)说是特征函数,那特征
实变函数里刚讲到勒贝格积分时,提到一个特征函数,f(x)=求和(ci*Xei(x))那个Xei(x)说是特征函数,那特征函数是什么意思,为什么是f(x),而不是f(x)的积分,就要用到求和了.
 爱我妞妞1年前1
爱我妞妞1年前1 -
 gznicholas 共回答了15个问题
gznicholas 共回答了15个问题 |采纳率86.7%集合的特征函数就是定义在这个集合内的点上的函数值为1,其他为01年前查看全部
- 谈谈对实变函数的认识.(可结合高等代数 近世代数作答) 不用大多 简答一下就行了
 小海飞刀1年前1
小海飞刀1年前1 -
 一指捕清风 共回答了23个问题
一指捕清风 共回答了23个问题 |采纳率91.3%实变函数就是实变量的函数,数学分析中微积分的那部分所讨论的函数都属于实变函数.所以要想学好实变函数,必须先学习数学分析.而近世代数(也叫抽象数学)是与密码学有关的一门学科,非常的难学!但我没发现其与实变函数有啥关系!
希望采纳1年前查看全部
大家在问
- 1第九届希望杯六年级复赛试题答案
- 2一道数学题,智者请进.
- 3已知在一个浴缸中放入400升水后浴缸留有1/3的空洞,则浴缸的容积为多少升?
- 4一道简单的锐角三角函数题角B=90度,角BDC=45度,COS角A=5/7,BD=4根号6,求AC
- 5生铁炼钢时在碳与氧气反应的同时,生铁中的铁是否也与氧气反应
- 6椭圆的2个焦点坐标是f1(-1,0),f2(-2,0)点p为椭圆的一点 ,∣f1f2∣是 ∣pf1∣和∣pf2∣的等差中
- 7英语翻译I came home at six yesterday.(改一般疑问句)He shopped the thie
- 8下列哪种物质能使酚酞变红Co2 CaCO3 Ca(OH)2
- 9高中生物密闭内某植物在黑暗中释放v(CO2)=22mg/h.在光照下吸收v(CO2)=44mg/h
- 10已知A(-2,0),B(2,0),点P在圆(x-3)2+(y-4)2=4上运动,则|PA|2+|PB|2的最小值是(
- 11修路队修一条公路,第一天修了200米,第二天修了300米,两天共修了总长的26/5,这条公路长多少米?
- 12新的一年,新的开始,我们走了新的计划 要怎么翻译。。各位学霸,求解!
- 13考CATTI,汉英大辞典和新世纪汉英大词典,哪个好?
- 14What present are they going to give to their friends?
- 15下列不属于互联网作用的是A.使信息的即时反馈得以实现B.人们上网可以随时发表自己的意见C.其普及削弱了其他媒介的地位D.
