同余方程求解通过直接验算,求x^2+8x-13≡0(mod 28)的解和解数,急,收到请速回复谢谢!
 loy2032022-10-04 11:39:542条回答
loy2032022-10-04 11:39:542条回答
已提交,审核后显示!提交回复
共2条回复
 gk8849 共回答了16个问题
gk8849 共回答了16个问题 |采纳率93.8%- 28=2^2*7
x^2+8x-13≡x^2+x+1 (mod7)
x≡0, 显然不符
x≡1, 代入得:1+1+1≡3, 不符
x≡-1,代入得:1-1+1≡1, 不符
x≡2, 代入得:4+2+1≡7≡0, 符合
x≡-2, 代入得;4-2+1≡3,不符
x≡3, 代入得:9+3+1≡-1, 不符
x≡-3, 代入得:9-3+1≡7≡0, 符合
x^2+8x-13≡x^2-1 (mod4)
得:x≡1 (mod2)
结合得原方程的解为x≡9, -3 (mod 14)
即x≡9, 23, 11, 25 (mod 28)
共4个解 - 1年前
 君子烧卖 共回答了160个问题
君子烧卖 共回答了160个问题 |采纳率- dennis_zyp|十七级 已经出很好的方法。
我补充一下。
求x^2+8x-13≡0(mod 28)的解和解数
配方得
(x+4)^2==1 mod 4*7
解之得x==-3或-5 mod 4
且x==-3或-5 mod 7.
于是得到:
x==-3或-5 mod 28
即x==25, ... - 1年前
相关推荐
- 同余方程组求解.甲乙港的距离不超过5000km,今有三只轮船于某天零时同时从甲港开往乙港,假定三只轮船每天24小时都是匀
同余方程组求解
.甲乙港的距离不超过5000km,今有三只轮船于某天零时同时从甲港开往乙港,假定三只轮船每天24小时都是匀速航行,若干天后的零时第一只轮船首先到达,几天后的18时第二只轮船也到达,再过几天后的8时第三只轮船也到达了.假如每天第一只轮船走300km,第二只轮船走240km,第三只轮船走180km,问甲乙两港实际距离是多少?三只轮船各走了多长时间? haoyun晶晶1年前3
haoyun晶晶1年前3 -
 taotian123 共回答了21个问题
taotian123 共回答了21个问题 |采纳率95.2%设三只船行驶的天数分别为X、Y、Z,其中X1年前查看全部
- 跪求大神帮忙做一道同余方程组的题!
跪求大神帮忙做一道同余方程组的题!
第3 题是求同余方程的所有的解, 第4 题是求该同余方程组的解, 谢谢了!


 hans10001年前2
hans10001年前2 -
 南浔小五 共回答了21个问题
南浔小五 共回答了21个问题 |采纳率100%题三:xx+3x+3==0 mod 169
169=13^2
先解xx+3x+3=0 mod 13
即xx-10x+25-22==0
(x-5)^2==22==9
于是x==8或2 mod 13
即x=8+13a (#1#) 或x=2+13b (#2#)
由 (#1#)得
169aa+13*16a+64+(24+39a)+3==0 mod 169
即13(19a+7)==0 mod 13*13
即19a+7==0 mod 13,即6a==-7==6,即a=1 + 13k
于是x=21 +169k ==21 mod 169
由 (#2#)得
169bb+4*13b+4+(6+39b)+3==0 mod 169
即13(7b+1)==0 mod 13*13
解得b==-2 mod 13, 即b=-2+13t
于是x=2+13(-2+13t)=-24 +169t, 即x==-24==145 mod 169
综上述,原二次同余式有两解,x==21或-24 mod 169
注:将21或-24代入均得到 507==0 mod 169.我想还有简便方法.
题四:x+3y==3 mod 11; 2x+y==3 mod 11
第一式乘2得,2x+6y==6 mod 11, 与第二式作差得5y==3 mod 11==25, 故y==5
代入得x==-3y+3==-12 ==-1
即原同余式组的解为 x==-1, y==5 mod 111年前查看全部
- 怎么解以下的同余方程问题?(敬求尽可能详细的讲解,因为本人数学学的不多,最好能给每一个步骤做详细的解释.)1.求以下同余
怎么解以下的同余方程问题?
(敬求尽可能详细的讲解,因为本人数学学的不多,最好能给每一个步骤做详细的解释.)
1.求以下同余方程组的最小四位正整数解.
x ≡ 1(mod 3)
x ≡ 2(mod 5)
x ≡ 3(mod 7)
2.求 1234x ≡ 33(mod 2013)的最小正整数解.
Tp:解同余方程需要注意哪些地方?
Tp II: 丁8索骨1年前1
丁8索骨1年前1 -
 123xuwei 共回答了20个问题
123xuwei 共回答了20个问题 |采纳率95%求以下同余方程组的最小四位正整数解.
x ≡ 1(mod 3)
x ≡ 2(mod 5)
x ≡ 3(mod 7)
70≡1 mod 3.(1)
21≡1 mod 5.(2)
15≡1 mod 7.(3)
由(1)得 490≡1 mod 3 且490≡0 mod 35
由(2)得 126≡1 mod 5 且126≡0 mod 21
由(3)得 120≡1 mod 7 且120≡0 mod 15
故最小的四位数是490×1+126×2+120×3=11021年前查看全部
- 什么是解同余方程啊?举个例子看看?举个稍微有代表性的例子
 啥都看1年前1
啥都看1年前1 -
 紫色 共回答了28个问题
紫色 共回答了28个问题 |采纳率85.7%同余方程就是指包含取余操作的整数方程.如 x=2 mod 3
典型的同余方程组就是韩信点兵问题:
x=2 mod 3
x=1 mod 5
x=4 mod 7
求x1年前查看全部
- 同余方程问题,数论高手请进证明5X²+11Y²≡1(mod m)对任何正整数m都有解
 spp8401061年前3
spp8401061年前3 -
 佛余额 共回答了19个问题
佛余额 共回答了19个问题 |采纳率94.7%首先考虑m为素数的情形
若5或11中有一个modm的二次剩余,不妨设为5
I={r1,r2,...r[(m+1)/2]}为modm的所有二次剩余
由勒让德符号定义的运算(或二次剩余的欧拉判别法)知,r1为二次剩余时5*r1亦为二次剩余
且5*ri不同余于5*rj,如果ri不等于rj
I1={5r1,5r2,...5r[(m+1)/2]}为modm的所有二次剩余
即5x^可以取I1中任意值
易知1属于I
则方程5X²≡1(mod m)有解,再取y=0即可
若5或11都不是modm的二次剩余
r1为二次剩余(r1非0)时5*r1和11*r1为二次非剩余
即I2={5r1,5r2,...5r[(m+1)/2]}为modm的所有二次非剩余和{0}的并集
下面应用反证法,若原方程无解
则I2/{0}中任意两元素和不为m+1
考虑下列(m-1)/2个集合
{2,m-1}{3,m-2}{(m-1)/2,(m+3)/2}和{(m+1)/2}
I2/{0}中(m-1)/2个元素皆取自此(m-1)/2个集合
若有一个集合中同时含有两个I2/{0}中元素
则方程5X²≡i(mod m)11Y²≡m+1-i(mod m)皆有解
原方程亦有解
若任一集合中不同时含有两个I2/{0}中元素
则(m+1)/2为I2/{0}中元素
方程5X²≡(m+1)/2(mod m)11Y²≡(m+1)/2(mod m)皆有解
原方程亦有解
以上证明了m为质数时方程有解
下面证明m为质数幂时方程有解
m=p^n,对指数n归纳(不考虑p=2,5,11时情形,这些情形的证明很容易)
n=k时成立,n=k+1时
5X²≡i+t*p^k(mod m)
计x1=x,x2=x+p^n,x3=x+2*p^n.xp=x+(p-1)p^n
以上p个数代入方程左端modm两两不同余,
必有一j使xj满足5xj^≡i(mod m)
对于11同理,则n=k+1时亦得证
对于一般的m,对m进行质因数分解,
m=p1^a1*p2^n2*...
计m1=p1^a1
m2=...
(xi,yi)为5xi^+11yi^≡1(mod mi)的解
考虑一次同余方程组
x=x1(modm1)
x=x2(modm2)
...(此处=为同余号)
由中国剩余定理
x有解
对y同理
于是(x,y)即为满足条件的解
初涉数论,如有漏洞请指出,欢迎切磋探讨.这道题真的很难,不知楼主是在哪里看到的?1年前查看全部
- 关于同余方程等价变形的问题“只要两者的解相同的变形就是等价变形,并不要求解数相同”请问这里两者解数不同为什么会有解相同呢
 renyuting1年前2
renyuting1年前2 -
 zhengruiyi 共回答了12个问题
zhengruiyi 共回答了12个问题 |采纳率100%题:关于同余方程等价变形的问题:“只要两者的解相同的变形就是等价变形,并不要求解数相同”
请问这里两者解数不同为什么会有解相同呢
举一个简例.3x==6 mod 9
它可以等价变形成x==2 mod 3
原式的解是基于模9的,解为x==2,5,8 mod 9
后者的解是基于模3的,解为x==2 mod 3
但是这两个解实际是相同的,它们的解集{2+9t,5+9t,8+9t;t为整数} 与 {2+3k;k为整数}是等价的集合.
另举一个:4x==8 mod 10 与 2x==4 mod 5 同解,而解数不同;
2x==4 mod 5与 x==2 mod 5同解,解数相同.
4x==8与 x==2 mod 5同解,解数不同.
具体分析从略.1年前查看全部
- 求解同余方程.一共两题
求解同余方程.

一共两题 dame孤雁1年前1
dame孤雁1年前1 -
 zlnannan 共回答了21个问题
zlnannan 共回答了21个问题 |采纳率85.7%3=3mod9
9=2mod7
3=3mod7
3*2+3=2mod7
3*9+3=30
30+63=93
x=93
2
11mod5=1
3mod5=3
4+3=2mod5
4*11+3=47
55=1mod3
2+47=1mod3
55*2+47=157
x=1571年前查看全部
- 关于同余方程的解(1)证明x(x+1)≡-1(mod17)无解(2)证明x(x+1)≡-1(mod59)无解特别是第2个
关于同余方程的解
(1)证明x(x+1)≡-1(mod17)无解
(2)证明x(x+1)≡-1(mod59)无解
特别是第2个,除了把1,2,3,...,29代入计算还有什么方法?
x(x+1)≡-1(mod31)就有解x≡5 dhdk1年前1
dhdk1年前1 -
 yangyajun8 共回答了24个问题
yangyajun8 共回答了24个问题 |采纳率91.7%这个要用二次剩余理论, 包括二次互反律.
对质数p, 以及p互质的整数a, 用(a|p)表示Legendre符号:
即当x² ≡ a (mod p)有解时, (a|p) = 1, 无解时(a|p) = -1.
(1) x(x+1) ≡ -1 (mod 17)等价于(2x+1)² = 4x(x+1)+1 ≡ -3 (mod 17).
只需要说明-3不是mod 17的二次剩余即可, 即(-3|17) = -1.
由17 ≡ 1 (mod 4), 可知(-1|17) = 1.
而(-3|17) = (-1|17)·(3|17), 于是只需说明(3|17) = -1.
这里由二次互反律, (3|17)·(17|3) = (-1)^((3-1)(17-1)/4) = 1,
得(3|17) = (17|3) = (2|3) = -1.
(2) x(x+1) ≡ -1 (mod 59)等价于(2x+1)² = 4x(x+1)+1 ≡ -3 (mod 59).
由59 ≡ 3 (mod 4), 可知(-1|59) = -1.
又由二次互反律, (3|59)·(59|3) = (-1)^((3-1)(59-1)/4) = -1.
故(3|59) = -(59|3) = -(2|3) = 1.
因此(-3|59) = (-1|59)·(3|59) = -1.
-3不是mod 59的二次剩余, 方程无解.
至于x(x+1) ≡ -1 (mod 31)有解, 可同样化为证明(-3|31) = 1.
类似上面过程有(-1|31) = -1, (3|31) = -(31|3) = -(1|3) = -1, 因此(-3|31) = (-1|31)·(3|31) = 1.
实际上, 述过程可以证明一般结果:
对于质数p > 3, x(x+1) ≡ -1 (mod p)有解当且仅当p ≡ 1 (mod 3).1年前查看全部
- 同余方程组解下列同余式组x三1(mod)7 3x三4(mod5) x三0(mod9)
 destiny341年前1
destiny341年前1 -
 greentim 共回答了20个问题
greentim 共回答了20个问题 |采纳率80%3x同余4(mod5)--> 2*3x同余2*4(mod5) --> x同余3(mod5),
x同余1(mod7) ,
x同余0(mod9) ,
x = ,(5*7*9)m + (7*9) + (5*7)*9 + (5*9)*5
= (5*7*9)M + 63 + 225
= (5*7*9)M + 288,1年前查看全部
- 6x≡3 (mod 10) 同余方程求解
6x≡3 (mod 10) 同余方程求解
我老是得到有分数,望高手指教
 smbin1年前1
smbin1年前1 -
 840817 共回答了20个问题
840817 共回答了20个问题 |采纳率85%无解
ax≡b (mod m)有解的充要条件是(a,m)|b
这里(6,10)=2,显然不能整除3,
所以无解1年前查看全部
- 关于同余方程到底什么是同余方程,我看一本书里的介绍看不懂,谁能用通俗的语言给我讲讲,还有那个mol是什么?,那些方程的式
关于同余方程
到底什么是同余方程,我看一本书里的介绍看不懂,谁能用通俗的语言给我讲讲,还有那个mol是什么?,那些方程的式子怎么看?
写错了,不是mol是mod,是数学的内容 aliang123141年前2
aliang123141年前2 -
 sunjie235 共回答了25个问题
sunjie235 共回答了25个问题 |采纳率88%同余,是极具有思想方法意义的.这个需要反思运用体会的.可以做很深入的解释,及推广.
这是我以前的回答,
对于一组整数Z,Z里的每一个数都除以同一个数m,得到的余数可以为0,1,2,...m-1,共m种.我们就以余数的大小作为标准将Z分为m类.每一类都有相同的余数.
在每一类下的任意两个数a,b都关于m同余.记为:
a=b(mod m)
用集合论的语言,严格地来说就是:
对于整数集的任意一个子集Z,对于任意一个属于Z的元素n,n都除以m,得到的余数的余数可以为0,1,2,...m-1,共m种.我们就以余数的大小作为标准,将Z分为m个互不相交的m个子集Z1,Z2,...Zm-1.
对于Zi的任意两个元素a,b,都关于m同余.记为
要停电了,我明天再给你解答吧.
a=b(mod m)
其实还可以用更数学化的语言来表达.
同余的运用
请问各位叔叔阿姨!若一个数除3余2,除5余3,除7余4,除11余5,求它的最小正整数?
0 - 解决时间:2006-2-21 21:45
最好有解题过程,
问题补充:368才对!
rodger001 - 试用期 一级
368
详细解题过程不容易表达清晰.看来是刚注册的,怪不得没有悬赏分.
那就讲思路吧.依次满足下面四个条件:
1.先满足除11余5,易知为16
2.再满足除7余4,16最多再加6个11,最后为60
3.再满足除5余3,60最多再加4个11×7,最后为368
4.再满足除3余2,最后为368.
判断条件是否满足时,用同余运算可简化.
如除5时,77与2同余,60再加4个2(或4个77),就能单独满足除5余3.这里60+4×77与60+4×2同余.但60+4×77是在满足前两个条件的前提下进行的.
回答者:林锦1983 - 见习魔法师 二级 2-20 23:15
--------------------------------------------------------------------------------
这是家教中遇到的,原来我读书的时候没有学这东西!但上面错了一个字,再加6个11应该是再加4个11.
--------------------------------------------------------------------------------
评价已经被关闭 目前有 4
好
75% (3) 不好
25% (1)
我说的是估算最大计算量,最多再加6个11,实际上只要加4个11就行了.同余运算是数论的基础知识,一般初中奥赛教材就有了.其实“同余概念”的基础是抽象分类法.这里仅抽取“余数的大小”这一抽象特性,作为分类的标准.1年前查看全部
- 关于数论同余方程问题是否存在一个素数p>=3,使得2^p≡2 mod p^2成立?
 qjinghong1年前1
qjinghong1年前1 -
 想回了 共回答了16个问题
想回了 共回答了16个问题 |采纳率75%存在,例p=1093 1093^2|2^1092 -1
另有:11^2|3^10-11年前查看全部
- 求同余方程x^5-3x^2+2≡0(mod 7),急,收到请速回复谢谢!
 cq7dj1年前2
cq7dj1年前2 -
 cheng314 共回答了22个问题
cheng314 共回答了22个问题 |采纳率86.4%设X=7K+m代入得:
(7K+m)^5-3(7K+m)^2+2≡0
展开得:(7K)^5+5*(7K)^4*m+10*(7k)^3*m^2+--+m^5-3(49k^2+14km+m^2)+2≡0(mod 7),
∵(7K)^5+5*(7K)^4*m+10*(7k)^3*m^2+--+49k^2+14km+m^2≡0(mod 7),
∴只要:m^5-3*m^2+2≡0(mod 7),
即:(m-1)(m^4+m^3+m^2-2m-2)≡0(mod 7),
∵当m=1时,m^5-3*m^2+2=0,显然有m^5-3*m^2+2≡0(mod 7),
当m=-2时,有16-8+4+4-2=14≡0(mod 7),
所以X=7K+1与X=7K-2都是同余方程x^5-3x^2+2≡0(mod 7)方程的解.
如X=1或5、8、12、15、19-------
前面已有了,再来一次?送分?1年前查看全部
- 为什么书上要用更复杂的形式表示同余方程的解,我认为,所有一元一次同余方程,不存在1个以上的解,只是形式上变复杂了,看上去
为什么书上要用更复杂的形式表示同余方程的解,我认为,所有一元一次同余方程,不存在1个以上的解,只是形式上变复杂了,看上去,有几个解如x=3(mod5)
与3,8,13(mod15)相同,说它有三个解好像没多大意义,那位解答我的疑问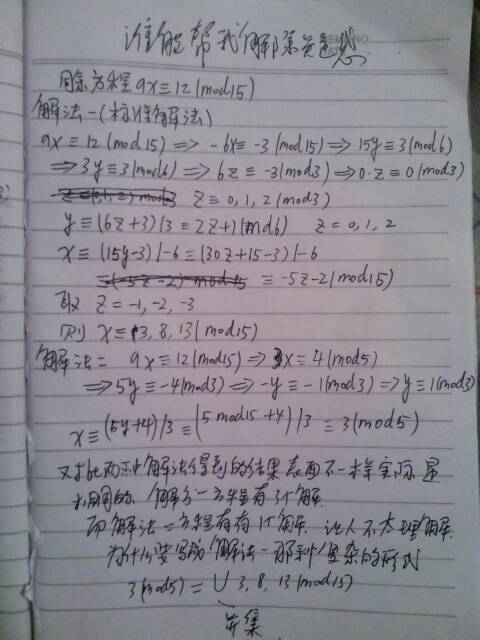
 germania1年前1
germania1年前1 -
 魔鬼的老大 共回答了21个问题
魔鬼的老大 共回答了21个问题 |采纳率100%举一个简例.3x==6 mod 9
它可以等价变形成x==2 mod 3
原式的解是基于模9的,解为x==2,5,8 mod 9
后者的解是基于模3的,解为x==2 mod 3
但是这两个解实际是相同的,它们的解集{2+9t,5+9t,8+9t;t为整数} 与 {2+3k;k为整数}是等价的集合.解集相同,说明解相同.其中一个,解集由三个子集构成,写成三个解的形式,称为三个解.另一个解集写成一个解.
解数不同,但是它们是同解的,或说他们的解相同.
x=3(mod5)与3,8,13(mod15),也是同解,但前者写成为一个解的形式,后者写成了三个解.
另举一个:4x==8 mod 10 与 2x==4 mod 5 同解,而解数不同;
2x==4 mod 5与 x==2 mod 5同解,解数相同.
4x==8与 x==2 mod 5同解,解数不同.1年前查看全部
- 中国剩余定理的同余方程组里的mod是什么意思
 livfang1年前1
livfang1年前1 -
 伊人家 共回答了15个问题
伊人家 共回答了15个问题 |采纳率100%要想了解更清楚,
可以搜索
wsktuuytyh 同余
wsktuuytyh 同余概念1年前查看全部
- 同余方程643x≡32(mod47)的解是______.
 86263551年前1
86263551年前1 -
 canniness 共回答了13个问题
canniness 共回答了13个问题 |采纳率92.3%(47*13+32)x≡32(mod47)
32x≡32(mod47)
32(x-1)≡0(mod(47)
x≡1(mod47)1年前查看全部
- 同余方程的解x≡3(mod7),x≡6(mod23),x≡12(mod31)怎么解?
 byy81030830221年前1
byy81030830221年前1 -
 一点浮云 共回答了14个问题
一点浮云 共回答了14个问题 |采纳率78.6%在古代中国的时候孙子就给出了这类题目的做法:“三人同行七十稀,五树梅花廿一枝,七子团圆月正半,除百零五便得知.”
这道题目用的方法其实一样:
除数7,23,31,最小公倍数就是7×23×31=4991,除7的余数是3,这样乘率就是6,;除以23的余数是6,这样乘率就是7,除以31的余数是12,这样乘率就是26.
把总和算出来:23×31×3×6+7×31×6×7+7×23×12×26=72180.,这是一个符合条件的数,72180-4991×14=2306是最小的数,x的所有解是:2306+4991k(k∈Z)1年前查看全部
- 同余方程组求解X==1 mod 2 X==2 mod 5 X==3 mod 7 X==4 mod 9
 binggan3211年前1
binggan3211年前1 -
 xidaodaodiannao 共回答了19个问题
xidaodaodiannao 共回答了19个问题 |采纳率94.7%首先算出除数2,5,7,9的最小公倍数
2*5*7*9=630
X==1 mod 2的乘率计算等于1
X==2 mod 5的乘率计算等于2
X==3 mod 7的乘率计算等于4
X==4 mod 9的乘率计算等于16
得到满足条件的最小正同余数为
5*7*9*1+2*7*9*2+2*5*9*4+2*5*7*16-630*3=157
所以解得X=157+630K K∈整数1年前查看全部
- 数论急求,在线等,有追加:假设p是一个奇素数.证明同余方程x^4≡-1(mod p)有解当且仅当p形如8k+1
 chuan19884271年前1
chuan19884271年前1 -
 keaiyue666 共回答了16个问题
keaiyue666 共回答了16个问题 |采纳率93.8%很显然这是一道原根题.设g为p的一个原根,那么p的简化剩余系可表示为g^0,g^1,g^2,...,g^phi(p).当然还有个小地方没解释,这个同余方程的解肯定是在p的简化剩余系中的,我想这个你要是也不知道的话估计更不知道什么是原根了,你自己想哦.方程转化为(g^i)^4≡-1.而-1在原根中的唯一表示是g^(phi(p)/2).那么方程再次转化为(g^i)^4≡g^(phi(p)/2).由原根指数的性质知:4i≡phi(p)/2(mod phi(p)).这样就证明了8|phi(p),那么p就有形如8k+1了.呵呵1年前查看全部
- 同余方程怎么解?比如31x=5(mod17),
 阳光6171211年前1
阳光6171211年前1 -
 duping007 共回答了14个问题
duping007 共回答了14个问题 |采纳率85.7%因为 31x≡34x-3x≡ -3x≡5(mod 17) ,
所以两边同乘以 6 得 -18x≡30≡13(mod 17) ,
因此 -x≡13(mod 17) ,
则 x≡ -13≡4(mod 17) .1年前查看全部
- 怎么解 模是素数的高阶同余方程例如 X^4+3X^3-X^2+X+1==0(mod7)这个的解,是只能把X=0.1.2.
怎么解 模是素数的高阶同余方程
例如 X^4+3X^3-X^2+X+1==0(mod7)
这个的解,是只能把X=0.1.2.3...6带进去看是否成立吗?
还有其他办法吗 23415qw1年前3
23415qw1年前3 -
 stevelong 共回答了12个问题
stevelong 共回答了12个问题 |采纳率91.7%由X^n==nX(mod7) (因为模是素数)
X^4+3X^3-X^2+X+1==0(mod7)
变为4X+9X-2X+X+1==0(mod7)
即12X+1==0(mod7)
则X==4(mod7)1年前查看全部
- 同余方程组解法刚刚搜到你对同余方程组的解法,感觉比较麻烦,也可能是看得不是很懂.对于一般的同余方程组的解法有哪些?上课没
同余方程组解法
刚刚搜到你对同余方程组的解法,感觉比较麻烦,也可能是看得不是很懂.对于一般的同余方程组的解法有哪些?上课没注意听. 在广州的冯坡人1年前1
在广州的冯坡人1年前1 -
 周珊珊 共回答了19个问题
周珊珊 共回答了19个问题 |采纳率94.7%我写个简例吧:
AAA解法:
解同余式组:x≡1(mod5) x≡2(mod11)
中国剩余定理的等效解法
令x=5a+11b +55t 亦即 x==5a+11b mod 5*11
代入原同余式组得
11b==1 mod 5
5a==2 mod 11
解得b==1 mod 5, a=-4==7 mod 11
取任意一组特解如b=1,a=7代入得
x==5*7+11*1=46 mod 55
BBB解的数量之判定法:
对于多个模并非两两互质的情况,可以先确立一组两两互质的分解基数集(质数集是一个常用的特例),将这些模用分解基数表示成为多个因数项,将其中相关于同一个分解基数的项进行归并.如果有矛盾,则无解.
否则有解.
例:同余式组
x=2 mod 16
x=3 mod 5
x=6 mod 12
取4, 3, 5作为分解基.变成
x=2 mod 4^2
x=3 mod 5
x=6 mod 4
x=6 mod 3
其中相关于同一个分解基数的情况,仅有x=2 mod 16与x=6 mod 4是相关于分解基数"4"的,它们没有矛盾.取两相容解集的交集,即其中解集较小的那个:x=2 mod 16.
再与x=3 mod 5及x=6==0 mod 3联立求解.
另例:
x=2 mod 18
x=8 mod 12
以3,2为分解基.
相关于分解基数3的转化式有x=2 mod 3^2, x=2 mod 3, 取前者.
相关于分解基数2的转化式有x=0 mod 2, x=0 mod 4, 取后者.
另例:同余式组
x=3 mod 12
x=2 mod 18
以2,3为分解基集,于是原同余式组变成
x==3 mod 2^2
x==3 mod 3
x==2 mod 3^2
x==2 mod 2
矛盾.故此同余式无解.
如果是形如
ax=b mod m形状的同余式联立的,
则可能出现无解、一解、多解的情况.一个基本的例子如下:
12x=18 mod 27 注:相当于12x=9+18k
自然就等价于同余式
4x=3 mod 9
解得x=3 mod 9, 转化为模27的同余式,为
x=3,12,21 mod 27
AAAAAA快速计算法
例如同余式组(以下用==表示同余号)
x==
2 mod 5
-2 mod 6
-3 mod 7
对中国剩余定理一个简单的改进可以是这样:
令
x=5*6*7*(a/5+b/6+c/7) mod 5*6*7
即x=6*7*a+5*7*b+5*6* c+ 5*6*7 t
代入原题即得
6*7*a==2 mod 5
5*7*b==-2 mod 6
5*6*c==-3 mod 7
求得
a==1 mod 3, 或者说是形如-1+3u的任意整数.
b=2 mod 5, ...
c=2 mod 7
剩下的就是如果计算出x来了.下面也给了简化方法.
从下面这个式子上看
x=5*6*7*(a/5+b/6+c/7) mod 5*6*7
=5*6*7*(a/5+b/6+c/7 mod 1) 注意,这个式子极具有启发性!
我们看到,我们需要的x的值,只要取以5*6*7作分母时的分数(a/5+b/6+c/7) 的分子就行了,
如果我们将 a/5+b/6+c/7表示成带分数,即整数加真分数的形式.
还可以发现,如果要取最小正整数解,就取这个真分数的分子就形子.
在计算过程中,
任意加减一个整数,造成数的增大和变小,并不影响我们的结果.
同时,任意交换加项,也不影响.
下面我们来计算:
1/5+2/6+2/7 mod 1=16/30+2/7=172/210
再例:这是我刚答的一道题,讲的较为明确精炼,请参考.
一个数÷5余1,÷7余3,÷9余2,这个数最小是几?
题目转化为同余式组
x==1 mod 5
x==3 mod 7
x==2 mod 9
令x==7*9*a+5*9*b+5*7*c mod 5*7*9
即x=7*9*a+5*9*b+5*7*c+5*7*9*t
即x==5*7*9*(a/5+b/7+c/9 mod 1)
即x=5*7*9*(a/5+b/7+c/9+t)
代入原同余式组得
7*9*a==1 mod 5 , 于是a==2 mod 5, 取其特值2为代表.
5*9*b ==3 mod 7,于是b==1 mod 7,取其特值1为代表.
5*7*c==2 mod 9,于是c==-2 mod 9,取其特值-2为代表.
再以
x==5*7*9*(a/5+b/7+c/9 mod 1)为求值式,进行计算.
先计算(a/5+b/7+c/9 mod 1)
注意,计算过程中,任一个加项或整体值上可以加减任一个整数,不影响.同时,在计算时,可以充分运用加法的交换律与结合律,随意调整加法项的位置与加法过程的顺序.
其中,mod 1这个提法一定要理解,这样可以为解同余式组带来极大的方便.
mod 1表示两个对象相差一个整数值.如果mod用来表示求余,则表示求一个数的小数部分;如果N==0 mod 1,即说明N为整数.
2/5+1/7-2/9 mod 1 ==2/5-2/9+1/7==8/45+1/7==101/45*7==101/315
于是x==101 mod 315
这个数最小为 1011年前查看全部
- 如何解同余方程?97v≡1(mod34)如何求最小的v?
 nn四夜1年前2
nn四夜1年前2 -
 bghe062gx0_875 共回答了14个问题
bghe062gx0_875 共回答了14个问题 |采纳率85.7%97同余于1(模数34)等同于(97-34*2=29)v同余于1(模数34),所以29*v/34余1.用辗转相除法求出6*34-7*29=1所以V=-7,所以V=-7+34K(K为整数)当K=1时V=27.1年前查看全部
- 一次同余方程是什么
 cicauto1年前1
cicauto1年前1 -
 ling723519 共回答了19个问题
ling723519 共回答了19个问题 |采纳率94.7%同余,是极具有思想方法意义的.这个需要反思运用体会的.可以做很深入的解释,及推广.
这是我以前的回答,
对于一组整数Z,Z里的每一个数都除以同一个数m,得到的余数可以为0,1,2,...m-1,共m种.我们就以余数的大小作为标准将Z分为m类.每一类都有相同的余数.
在每一类下的任意两个数a,b都关于m同余.记为:
a=b(mod m)
用集合论的语言,严格地来说就是:
对于整数集的任意一个子集Z,对于任意一个属于Z的元素n,n都除以m,得到的余数的余数可以为0,1,2,...m-1,共m种.我们就以余数的大小作为标准,将Z分为m个互不相交的m个子集Z1,Z2,...Zm-1.
对于Zi的任意两个元素a,b,都关于m同余.1年前查看全部
- 如何解如下同余方程组:4=(3a+14b)(mod 26) (1) 13=(13a+19b) (mod 26) (2)
 sfy00431年前1
sfy00431年前1 -
 ysy21 共回答了21个问题
ysy21 共回答了21个问题 |采纳率85.7%这是一个线性方程组,可以类比一般的线性方程组进行求解,只是要在mod 26的剩余类环上运算.
用消元法.
由(2)-4·(1)得a-11b = -3 (mod 26) (3).
(1)-3·(3)得-5b = 13 (mod 26),乘以5得b = 13 (mod 26).
代回(3)得a = 10 (mod 26).
这种解法不是很系统.如果学了矩阵,可以写出方程组的系数矩阵A =
3 14
13 19
行列式3·19-13·14 = 5 (mod 26).
由5·(-5) = 1 (mod 26),5 (mod 26)的倒数就是-5 (mod 26).
系数矩阵的伴随矩阵A* =
19 -14
-13 3
系数矩阵的逆矩阵为A^(-1) = |A|^(-1)·A* =
9 18
13 11
于是向量(a,b)^T = A^(-1)·(4,13)^T = (10,13)^T.
即方程组的解为a = 10 (mod 26),b = 13 (mod 26).1年前查看全部
- 关于一次非标准同余方程组的的解法:形如 y=k[i]m[i]+r[i]的方程组中,若r[i]间相互不互质,
 bb0501221年前1
bb0501221年前1 -
 上海夜的颜色 共回答了15个问题
上海夜的颜色 共回答了15个问题 |采纳率93.3%写出系数矩阵行列式,让其为零,求出的K即为所求,1年前查看全部
- 英语翻译本文从E-筛法(Eratosthenes筛法的变形)出发,利用同余方程组工具和中国剩余定理得出了一个重要结论:E
英语翻译
本文从E-筛法(Eratosthenes筛法的变形)出发,利用同余方程组工具和中国剩余定理得出了一个重要结论:E-筛法中,在素数p这一步过滤掉了1/p比例的数.这个结论说明了连续素数列是归1列.接着我们讨论的归1列的一些性质,并研究了数列的归1性与数列的增长速度之间的关系,这是本文的一个重要内容,我们寄希望于连续素数列是增速最快的归1列,但到目前尚未得出定论.在文章最后,给出了几个遗留的问题. 咪噜咪噜8191年前4
咪噜咪噜8191年前4 -
 caiji211 共回答了18个问题
caiji211 共回答了18个问题 |采纳率94.4%This textual,set out from the E-screening method (deform of Eratosthenes sieve method ) ,using congruence equations tools and the Chinese remainder theorem can get a important conclusion:In E-sieve method,this step prime p to filter out the 1 / p proportion of the number.The conclusion shows that the consecutive prime is (the list for unitary columns归1列 术语 实在是不知道怎么翻了).Then we discuss some qualities of qualitythe sequence and research the relationship between the sequence`s polarity and the sequence`s increment speed,this is one of the important content in the textual ,we hope the prime sequence is the fastest growththe of list for unitary columns,but it still remains a problem now.At the end of the textual,give us a couple of loose ends to hited.
累死偶了····· ove1年前查看全部
- poj 2115 简单数论题,同余方程
poj 2115 简单数论题,同余方程
/*poj 2115*/
#include
using namespace std;
long long d;
void ex_euclid(long long a,long long b,long long &x,long long &y)
{
x05if(b==0)
x05{
x05x05x=1;
x05x05y=0;
x05x05d=a;
x05x05return;
x05}
x05ex_euclid(b,a%b,x,y);
x05long long t=x;
x05x=y;
x05y=t-(a/b)*y;
}
/* c * x = b - a mod (2 ^ k) */
int main()
{
x05long long a,b,x,c,y;
x05int k;
x05while(cin>>a>>b>>c>>k)
x05{
x05x05if (a == 0 && b == 0 && c == 0 && k == 0)
break;
x05x05long long m=(1 鱼翔浅底881年前1
鱼翔浅底881年前1 -
 意无止境 共回答了18个问题
意无止境 共回答了18个问题 |采纳率94.4%有个细节你没注意到,看到范围是11年前查看全部
- 同余方程组求解!解同余方程组:x≡6(mod11) x≡3(mod 8 ) x≡11(mod20)急,收到请速回复谢谢!
 kuaileruyang1年前3
kuaileruyang1年前3 -
 cwjyoyo 共回答了15个问题
cwjyoyo 共回答了15个问题 |采纳率93.3%解同余方程组:x≡6(mod11) x≡3(mod 8 ) x≡11(mod20)
等效于同余式组
(
x==6 mod 11 (#1#)
x==3 mod 8 (#2#)
x==11 mod 4 (#3#)
x==11 mod 5 (#4#)
其中,用==表示同余号.
)
即求他们的解集的交集.
其中 (#2#)的解集是(#3#)的解集的真子集.故原同余式组等效于
(
x==6 mod 11 (#1#)
x==3 mod 8 (#2#)
x==1 mod 5 (#4#转化而来)
)
后文详解得答案为
x==171 mod 440.
过程如下:
x==
(6/ (8*5) mod 11) *8*5+
(3/ (11*5) mod 8) *11*5+
(1/ (11*8) mod 5) *11*8
(
注1:其中 x== b/a mod m 用来简化表示 ax == b mod m.我首次见到是在洪伯阳先生的著作中,我常称之为洪伯阳同余表示.在其分子与分母上可以使用同余性质、比例性质、带分数性质即作为假分数、带分数来处理等等.后来发现其他著作中也有,时间先后我没有考证.
下面为表达与计算上的方便,采用我个人引入的模积表示法.我察觉到其形式的对称性,并考虑到了计算的对称性及其同余本质,十分方便计算.以下使用模积表示式进行计算.
注2:上式简化表示为以下形式,称为模积表示.为方便理解写了很多.实际上,有很多过程用心算来完成,可以快速得解.
(
6/ (8*5) @ 11)
3/ (11*5) @ 8)
1/ (11*8) @ 5
)
)
==
6/ -4 @ 11
3/-1 @ 8
1/3 @5
==
-3/2==(-3+11)/2=4 @ 11
-3 @ 8
(1+5)/3=2 @ 5
==
4 @ 11
-3 @ 8
2 @ 5
==
4*8-3*11 @ 8*11
2 @5
==
-1 @ 88
2 @ 5
==
176-5 mod 88*5
==171 mod 440
理解了这种方法,对中国剩余定理的本质就更深入一步了.
更多资料,请百度搜索
wsktuuytyh 模积计数法
或
wsktuuytyh 洪伯阳同余表示
或
wsktuuytyh 不定方程
(注:其中来源我的现有姓名何冬州的五笔编码)
事实上,容易看出等效于
x==
6 mod 11
11 mod 8
11 mod 20
==
6 mod 11
11 mod 40
==
11+
(y==
-5 mod 11
0 mod 40
)
y==
-5/40 @ 11
0/11 @ 40
==
6/-4 @ 11
0 @ 40
==
4 @ 11
0 @ 40
==160
X==11+Y==171 MOD 4401年前查看全部
- n^2+n+24可被 2010整除的同余方程解法
 qingfengxing1年前1
qingfengxing1年前1 -
 Steven18 共回答了19个问题
Steven18 共回答了19个问题 |采纳率89.5%nn+n+24==0 mod 2010
它的解是
4(nn+n+24)==0 mod 2010的一部分.
先解后者,再代回检验,剔去增解即可.
(2n+1)^2+95==0 mod 2010
记y=2n+1,即有yy==-95 mod 2010
易见y==0 mod 5,令y==5z,即有25zz==-95 mod 2010,即5zz==-19 mod 402
402=2*3*67,故zz=1 mod 2,5zz=-1 mod 3,5zz==-19 mod 67
即z==1 mod 2,z==1或-1 mod 3,zz==(-19-67*3)/5=-44==23 mod 67
故4zz==92==25 mod 67,故2z==5或-5 mod 67
z=36或31 mod 67
由
2n+1=5z,z==1 mod 2,z==1或-1 mod 3,z=36或31 mod 67,逆用中国剩余定理,得种4种解,再回代.略.1年前查看全部
大家在问
- 1谁有周记啊!给我发一篇,第一的肯定采纳!
- 2换元积分法求 急不定积分 dx/x^2-2x+3 用换元积分法求
- 3玉树琼花什么意思
- 4如图,△ABC的三个顶点分别在格子的3个顶点上,请你试着再在图中的格子的顶点上找出一个点D,使得△DBC与△ABC全等,
- 51/1X2X3十1/2X3x4十…1/16X17X18
- 6初二英语我不相信明天天气会晴的.I ( ) believe ir ( ) ( )sunny tomorrow.我会尽力去
- 7初一下册英语练习题三、完形填空.There__1__three people in my family------my
- 8下列关于反应热的表述正确的是( )
- 9一次函数.正比例函数怎么求解析式
- 10光的衍射现象是什么?
- 11During the Spring Festival, nothing can stop people ___
- 12帮我出10道简单的关于六年级上册学过的知识的填空题 要有答案写出来哦
- 13下图是在光学显微镜下观察到的洋葱根尖的图像,请分析回答: (1)图像B是在_______物镜下观察到的图像,要观察根尖细
- 14英语翻译我知道issued and outstanding 有发行流通的意思,还有其他意思吗?因为当outstandin
- 15关于水的组成的叙述中,正确的是( )
