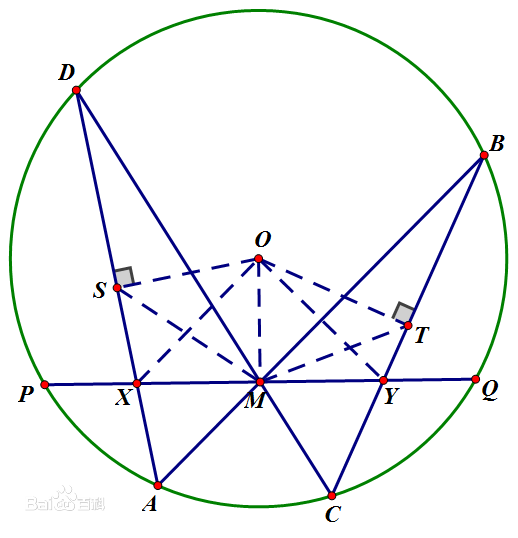
蝴蝶定理是不是能用在任意一个四边形里
 linuxl2022-10-04 11:39:542条回答
linuxl2022-10-04 11:39:542条回答
已提交,审核后显示!提交回复
共2条回复
 yaja_lisa 共回答了21个问题
yaja_lisa 共回答了21个问题 |采纳率85.7%- 不能、
- 1年前
 外围 共回答了22个问题
外围 共回答了22个问题 |采纳率81.8%- 不一定
- 1年前
相关推荐
- 只有等腰梯形里才有蝴蝶定理吗?其它梯形里有蝴蝶定理吗?急
 olbgj1年前1
olbgj1年前1 -
 xcdzw 共回答了21个问题
xcdzw 共回答了21个问题 |采纳率76.2%所以梯形都有蝴蝶定理1年前查看全部
- 第九题,网上的蝴蝶定理我看不懂,求cde面积
 生活好烦1年前1
生活好烦1年前1 -
 枪枪三人行 共回答了24个问题
枪枪三人行 共回答了24个问题 |采纳率91.7%先看△ADE和△ABE,不难发现,当两者分别以DE和BE为低时,高是相等的,所以DE是BE的1.5倍.
再看△ABD和△ABC,是同底(AB为公共底边)等高的,所以两者的面积相等.所以△BEC的面积等于△ADE的面积,即△BEC的面积等于3.
最后看△BEC和△CDE,当两者分别以BE和DE为低时,高是相等的,所以△CDE的面积是△BEC面积的1.5倍(DE是BE的1.5倍),即面积为4.5.1年前查看全部
- "蝴蝶定理"的证明
 qq1236541年前0
qq1236541年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 梯形的蝴蝶定理是什么(图)说得清楚点,为什么梯形中对称的连个三角形面积相等,我实在搞不清楚那个,我刚才知道了.现有浓度百
梯形的蝴蝶定理是什么(图)
说得清楚点,为什么梯形中对称的连个三角形面积相等,我实在搞不清楚
那个,我刚才知道了.现有浓度百分之十的盐水八千克,要得到浓度为百分之二十的盐水,要价高浓度盐水,用什么方法可以得到?(要有过程)这个问题就不用回答了!二楼那位有毛病啊,不问清楚瞎说什么!还有别的方法吗? dragon30701年前1
dragon30701年前1 -
 ryklts 共回答了19个问题
ryklts 共回答了19个问题 |采纳率89.5%因为两个三角形对称,所以全等1年前查看全部
- 数学竞赛中蝴蝶定理是什么?
 5040031年前0
5040031年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 【高中】关于圆的所有定理注意是高中,简单的初中定理不要说了,比如切线长定理不要说啦麻烦要解释清楚比如蝴蝶定理托勒密定理欧
【高中】关于圆的所有定理
注意是高中,简单的初中定理不要说了,比如切线长定理不要说啦
麻烦要解释清楚
比如蝴蝶定理
托勒密定理
欧拉定理
等等
我找到了。相交弦定理:圆内两弦相交,交点分得的两条线段的乘积相等
3)切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项
谁来证明一下这个2个定理 jl791年前1
jl791年前1 -
 yinshan56 共回答了11个问题
yinshan56 共回答了11个问题 |采纳率90.9%那些定理高中也不学,都是课外读物,
切割线定理高中会讲的
相交线定理比较简单,利用同弧所对的圆周角相等,证明两个三角形相似就可以了.
切割线定理,也是一次相似,初中学过弦切角吗?如果学过.一次就可以解决.1年前查看全部
- 数学竞赛中蝴蝶定理的证发,求大神
 好事佬1年前1
好事佬1年前1 -
 teresapeng 共回答了17个问题
teresapeng 共回答了17个问题 |采纳率88.2%1年前查看全部
- 蝴蝶定理的内容及证明过程?这个定理是谁提出来的?
 mx12341年前1
mx12341年前1 -
 alex_blue 共回答了15个问题
alex_blue 共回答了15个问题 |采纳率86.7%蝴蝶定理
自从学习几何画板以来,我一直在思索着这样一个问题:怎么才能把“蝴蝶定理”推广一下.
我想,能不能把“蝴蝶定理”中的圆由一个变为两个,相应的,还保持一种美妙的性质呢?如图I,是“蝴蝶定理”,有结论EP=PF;如图II,是“蝴蝶定理”的演变,点P,Q,R,S是否也存在某种关系呢?
我在课下做了一个比较精确的图,并进行了测量,进而提出了猜测:QM*PM = MS*MR,或者QM+PM = MS+MR.我又做了几个图进行检验,结果误差都比较小.上机时,利用几何画板做了一个动画,发现误差变化范围很大.我就开始怀疑这个结论.但是我并不死心.我又进行了测算,终于发现等式:成立,其误差在千分位之后.而后给出了一个数学上的证明.
这件事使我感觉到几何画板有以下几个妙处:比手工做图方便、精确、直观、连续.
如图I,取圆O内一条弦的中点P,过P点作AB、CD交圆于A、B、C、D点,连AD、BC交弦于E、F点,则EP=PF.这就是著名的“蝴蝶定理”.
题目:过圆心O的两个同心圆内弦中点M作两条直线交圆于A、B、C、D、E、F、G、H,连AF、BE、CH、DG分别交弦于点P、Q、R、S,则有等式:成立.这就是蝴蝶定理的推广.
证明:引理,如右图,有结论
由及正弦定理即可得到:
原结论
作OM1AD于M1,OM2EH于M2,
于是,MA - MD = MB - MC = 2MM1 = 2Msin;
MH - ME = MG - MF = 2MM2 = 2Msin
且MA*MD = ME*MH,MB*MC = MF*MG,代入上式,又
故原式成立
证毕.
关于“广义蝴蝶定理”的认识是在自己数学知识的基础上,借助于GSP而独立完成的.抛开广义蝴蝶定理自身的意义不论,单凭其处理问题的过程:推测、猜想、验证、论证,这不能不说是为中学数学教育留下某种思考,对中学生创造力的培养提供某种借鉴.1年前查看全部
- 蝴蝶定理的证明
 Z_T_MO1年前0
Z_T_MO1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 谁知道四边形蝴蝶定理的证明方法?
 我也是mopper1年前1
我也是mopper1年前1 -
 182yes 共回答了25个问题
182yes 共回答了25个问题 |采纳率88%可以提醒你一下:目前最简单的办法是运用解析几何,也就是建立坐标系啦,不过还是很烦的,我就不写了,
如果想知道的话可以到高中竞赛书上查查.1年前查看全部
- 25题,我知道这是蝴蝶定理,
25题,我知道这是蝴蝶定理,

 1984dd1年前1
1984dd1年前1 -
 Uivian 共回答了22个问题
Uivian 共回答了22个问题 |采纳率100%∵∠B+∠BCF=∠F+∠FEB,∠D+∠DEF=∠F+∠FCD 两式相加∵∠B+∠BCF+∠D+∠DEF==∠F+∠FEB+∠F+∠FCD ∵∠BCF=∠FCD,∠BEF=∠DEF ∴∠B+∠D=2∠F当∠B:∠D:∠F=2:4:x时,2+4=2x,解得x=31年前查看全部
- 蝴蝶定理的初等数学证明如题,蝴蝶定理的简单证明书上那个证明太高深了……看不懂……如果没有讲一下思路也好
 雨白瓜1年前1
雨白瓜1年前1 -
 秋闻妍 共回答了20个问题
秋闻妍 共回答了20个问题 |采纳率90%这里的解释很详细.1年前查看全部
- 直角梯形定理求证明,感觉长得有点像蝴蝶定理
直角梯形定理求证明,感觉长得有点像蝴蝶定理
在直角梯形ABCD中,角ADC=角BAD=90度.AB平行CD,AD是直角边.连接AC、BD,设交点为E,过E做AB与CD的平行线,分别交AD、BC于M、N,则有EM=EN.
老师说这个是定理,恒成立,求证明 linmeimei_lei1年前0
linmeimei_lei1年前0 -
 共回答了个问题
共回答了个问题 |采纳率
- 蝴蝶定理以下证明中为什么∠MOX=∠MOY?用的什么定理
蝴蝶定理以下证明中为什么∠MOX=∠MOY?用的什么定理
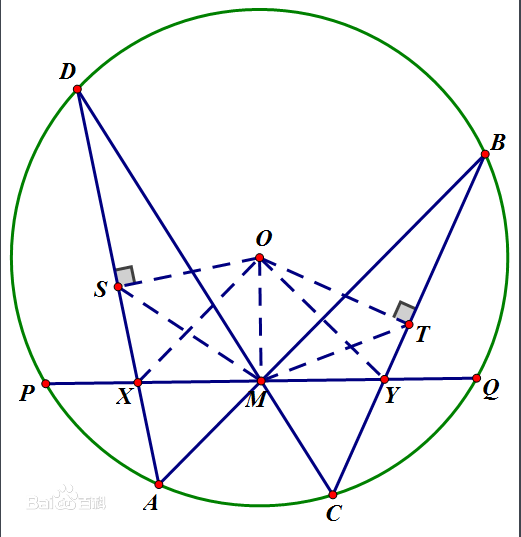
证明:过圆心O作AD与BC的垂线,垂足为S、T,连接OX,OY,OM,SM,MT.
∵OS⊥DA
∴∠OSD=90°
∵M为PQ中点
蝴蝶定理的证明
∴∠OMP=90°
∴∠OSD=∠OMP=90°
∴O,S,X,M四点共圆
同理,O,T,Y,M四点共圆
∴∠MTY=∠MOY,∠MSX=∠MOX
∴∠MOX=∠MOY ,
∵OM⊥PQ
∴∠OMX=∠OMY=90°
又OM=OM
∴△OMX≌△OMY
∴XM=YM lv倩1年前1
lv倩1年前1 -
 那小静 共回答了22个问题
那小静 共回答了22个问题 |采纳率95.5%∵∠D=∠B,∠A=∠C,∠AMD=∠CMB,
∴ΔDAM∽ΔBCM,∴AM/CD=AS/CB,
∴AM/CM=AS/CT,∴ΔSAM∽ΔTCM,
∴∠MSX=∠MTY,∴∠MOX=∠MOY.1年前查看全部
- 求上海西南模范初中的初一平面几何?(如蝴蝶定理,等积模型,鸟头定理等)试题,
 kealyzlf1年前2
kealyzlf1年前2 -
 飞扬1860 共回答了15个问题
飞扬1860 共回答了15个问题 |采纳率93.3%一、等积变换模型
1、等底等高的两个三角形面积相等.
2、两个三角形高相等,面积比等于它们的底之比.
3、两个三角形底相等,面积比等于它的的高之比.
二、共角定理模型
两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形.
共角三角形的面积比等到于对应角(相等角或互补角)两夹边的乘积之比.
三、蝴蝶定理模型
(说明:任意四边形与四边形、长方形、梯形,连接对角线所成四部的比例关系是一样的.)
四、相似三角形模型
相似三角形:是形状相同,但大小不同的三角形叫相似三角形.
相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比.
相似三角形的面积比等于它们相似比的平方.
五、燕尾定理模型
图片
bf:fc=bfd:fdc=abd:adc1年前查看全部
- 求用张角定理去证明蝴蝶定理.
 xhhaier1年前1
xhhaier1年前1 -
 liufanienck 共回答了16个问题
liufanienck 共回答了16个问题 |采纳率93.8%解法5 用张角定理证明蝴蝶定理.,1年前查看全部
- 蝴蝶定理最简单的证法
 130541835391年前3
130541835391年前3 -
 副巴戟 共回答了17个问题
副巴戟 共回答了17个问题 |采纳率88.2%http://baike.baidu.com/view/64379.htm1年前查看全部
- 蝴蝶定理共有多少种证明
 liqing27001年前1
liqing27001年前1 -
 乔丹一世 共回答了21个问题
乔丹一世 共回答了21个问题 |采纳率90.5%这里介绍一种较为简便的初等数学证法.
证明:过圆心O作AD与BC的垂线,垂足为S、T,连接OX,OY,OM,SM,MT.蝴蝶定理∵△AMD∽△CMB
∴AM/CM=AD/BC
∵AS=1/2AD,BT=1/2BC
∴AM/CM=AS/CT
又∵∠A=∠C
∴△AMS∽△CMT
∴∠MSX=∠MTY
∵∠OMX=∠OSX=90°
∴∠OMX+∠OSX=180°
∴O,S,X,M四点共圆
同理,O,T,Y,M四点共圆
∴∠MTY=∠MOY,∠MSX=∠MOX
∴∠MOX=∠MOY ,
∵OM⊥PQ
∴XM=YM
[1]其它证明方法:(注:²是平方的意思) 修改上图令 x = XM ,a = PM
则 AX · XD = PX · XQ = a² - x²
在 ΔDXM 中,由正弦定理:
DX = x·sin(α)/sin(180° - (α + β + γ)) = x·sin(α)/sin(α + β + γ).
在 ΔAXM 中:AX = x·sin(β)/sin(γ)
所以有
AX · DX = x²·sin(α)·sin(β)/sin(γ)·sin(α + β + γ) = a² - x²
∴ x² = a²·sin(γ)·sin(α + β + γ))/(sin(α)·sin(β) + sin(γ)·sin(α + β + γ))
在上面的式子中,α 和 β 是对称的.如果我们令 y = MY,会得到同样的结果
∴ x = y,得证
这个定理在椭圆中也成立,如图
1,椭圆的长轴A1、A2与x轴平行,短轴B1B2在y轴上,中心为M(o,r)(b>r>0).
(Ⅰ)写出椭圆的方程,求椭圆的焦点坐标及离心率
(Ⅱ)直线y=k1x交椭圆于两点C(x1,y1),D(x2,y2)(y2>0);直线y=k2x交椭圆于两点G(x3,y3),H(x4,y4)(y4>0).
求证:k1x1x2/(x1+x2)=k2x3x4/(x3+x4)
(Ⅲ)对于(Ⅱ)中的C,D,G,H,设CH交X轴于点P,GD交X轴于点Q.
求证:| OP | = | OQ |.
(证明过程不考虑CH或GD垂直于X轴的情形)1年前查看全部
- 蝴蝶定理:椭圆情形,几何法证明?
 kuhhn1年前1
kuhhn1年前1 -
 战龙无悔 共回答了21个问题
战龙无悔 共回答了21个问题 |采纳率85.7%圆锥曲线中涉及到焦点问题运用几何意义比较多,如果不涉及焦点,要运用几何法来证明问题就有难度了,事实上圆锥曲线放在解析几何的内容中进行研究,这是因为解析几何可以解决更多问题.你要证明椭圆中的蝴蝶定理,这个用几何法来证明应该是有困难的,至少我在资料上几乎没看到.筝形内的蝴蝶定理倒是可以用几何法证明也比较简单.欢迎追问1年前查看全部
- 求蝴蝶定理内容
 tpgjf1年前1
tpgjf1年前1 -
 shanghairen1983 共回答了15个问题
shanghairen1983 共回答了15个问题 |采纳率93.3%M为弦PQ的中点,AB和CD为过M点的另外两条弦.
AC,BD的连线交PQ于XY
则线段XY的中点为M.1年前查看全部
- 2011 四川高考数学卷的第21题 解析几何的 第二小问 如果用蝴蝶定理来求证 该怎样解答? PLEASE。
 枫尘幻风1年前2
枫尘幻风1年前2 -
 wjfsjk789 共回答了20个问题
wjfsjk789 共回答了20个问题 |采纳率80%蝴蝶定理是??我们没学过,河南的!1年前查看全部
- 蝴蝶定理证明过程中的疑问一种证明:令 x = XM , a = PM 则 AX · XD = PX · XQ
蝴蝶定理证明过程中的疑问
一种证明:令 x = XM , a = PM
则 AX · XD = PX · XQ = a² - x²
在 ΔDXM 中,由正弦定理:
DX = x·sin(α)/sin(180° - (α + β + γ)) = x·sin(α)/sin(α + β + γ).
在 ΔAXM 中: AX = x·sin(β)/sin(γ)
所以有
AX · DX = x²·sin(α)·sin(β)/sin(γ)·sin(α + β + γ) = a² - x²
∴ x² = a²·sin(γ)·sin(α + β + γ))/(sin(α)·sin(β) + sin(γ)·sin(α + β + γ))
在上面的式子中, α 和 β 是对称的. 如果我们令 y = MY,会得到同样的结果
∴ x = y,得证图中α,β,γ都分别是哪个角?
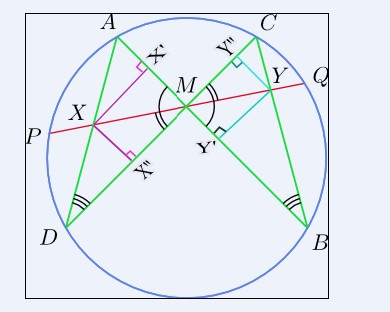
 一粒米粒1年前1
一粒米粒1年前1 -
 Z笑尘 共回答了15个问题
Z笑尘 共回答了15个问题 |采纳率100%α=∠XMD β=∠XMA γ=∠A
好诡异的证明1年前查看全部
- 一道几何证明题蝴蝶定理的解析法证明
 银河iiii地区1年前1
银河iiii地区1年前1 -
 超级呆呆 共回答了21个问题
超级呆呆 共回答了21个问题 |采纳率85.7%蝴蝶定理最先是作为一个征求证明的问题,刊载于1815年的一份通俗杂志《男士日记》上.由于其几何图形形象奇特、貌似蝴蝶,便以此命名,定理内容:圆O中的弦PQ的中点M,任作两弦AB,CD,弦AD与BC分别交PQ于X,Y,则M为XY之中点.
出现过许多优美奇特的解法,其中最早的,应首推霍纳在职815年所给出的证法.至于初等数学的证法,在国外资料中,一般都认为是由一位中学教师斯特温首先提出的,它给予出的是面积证法,其中应用了面积公式:S=1/2 BCSINA.1985年,在河南省《数学教师》创刊号上,杜锡录同志以《平面几何中的名题及其妙解》为题,载文向国内介绍蝴蝶定理,从此蝴蝶定理在神州大地到处传开.
这里介绍一种较为简便的初等数学证法.
证明:过圆心O作AD与B牟垂线,垂足为S、T,连接OX,OY,OM,SM,MT.
∵△AMD∽△CMB
∴AM/CM=AD/BC
∵SD=1/2AD,BT=1/2BC
∴AM/CM=AS/CT
又∵∠A=∠C
∴△AMS∽△CMT
∴∠MSX=∠MTY
∵∠OMX=∠OSX=90°
∴∠OMX+∠OSX=180°
∴O,S,X,M四点共圆
同理,O,T,Y,M四点共圆
∴∠MTY=∠MOY,∠MSX=∠MOX
∴∠MOX=∠MOY ,
∵OM⊥PQ
∴XM=YM
如图1,椭圆的长轴A1A2与x轴平行,短轴B1B2在y轴上,中心为M(o,r)(b>r>0).
(Ⅰ)写出椭圆的方程,求椭圆的焦点坐标及离心率;
(Ⅱ)直线y=kx交椭圆于两点C(x1,y1),D(x2,y2)(y2>0);直线y=k2x交椭圆于两点G(x3,y3),H(x4,y4)(y4>0).
求证:k1x1x2/(x1+x2)=k2x3x4/(x3+x4)
(Ⅲ)对于(Ⅱ)中的C,D,G,H,设CH交X轴于点P,GD交X轴于点Q.
求证: | OP | = | OQ |.
(证明过程不考虑CH或GD垂直于X轴的情形)
2.北京教育考试院招生考试办公室专家在公布的《2003年全国普通高等学校招生统一考试试题答案汇编》中给出的参考解答如下:
(18)本小题主要考查直线与椭圆的基本知识,考查分析问题和解决问题的能力.满分15分.
(Ⅰ)椭圆方程为x2/a2+(y-r)2/b2=1
焦点坐标为
(Ⅱ)证明:将直线CD的方程y=kx代入椭圆方程,得b2x2+a2(k1x-r)2=a2b2,
整理,得
(b2+a2k12)x2-2k1a2rx+(a2r2-a2b2)=0
根据韦达定理,得
x1+x2=2k1a2r/(b2+a2k12), x1·x2=(a2r2-a2b2)/( b2+a2k12),
所以x1x2/(x1+x2)=( r2-b2)/2k1r ①
将直线GH的方程y=k2x代入椭圆方程,同理可得
x3x4/(x3+x4)=( r2-b2)/2k2r ②
由①,②得k1x1x2/(x1+x2)=(r2-b2/2r=k2x3x4/(x3+x4)
所以结论成立.
(Ⅲ)证明:设点P(p,o),点Q(q,o).
由C,P,H共线,得
(x1-p)/( x4-p)=k1x1/k2x4
解得P=(k1-k2)x2x4/(k1x1-k2x4)
由D,Q,G共线,同理可得
q=(k1-k2)x2x3/(k1x2-k2x3)
由k1x1x2/(x1+x2)=k2x3x4/(x3+x4),变形得:
x2x3/(k1x2-k2x3)=x1x4/(k1x1-k2x4)
即:(k1-k2)x2x3/(k1x2-k2x3)=(k1-k2)x1x4/(k1x1-k2x4)
所以 |p|=|q|,即,|OP|=|OQ|.
3.简评
本小题主要考查直线与椭圆等基本知识,考查分析问题和解决问题的能力.试题入门容易,第(Ⅰ)问考查椭圆方程、待定系数法、坐标平移和椭圆性质:焦点坐标、离心率、看图说话即可解决问题,但考查的却都是重点内容.
第(Ⅱ)问是典型的直线与椭圆的位置关系问题.待证式子中含有x1x2,x1+x2,x3x4,x3+x4这样的对称式,式子结构对称优美,和谐平衡,使人很容易联想起一元二次方程根与系数关系的韦达定理,启示了证明问题的思路.这里用到了解析几何最根本的思想和最根本的方法.解两个联立的二元二次方程组,用代入消元法得到一元二次方程,分离系数利用韦达定理给出关于x1x2,x1+x2,x3x4,x3+x4的表达式,再分别代入待证式两边运算即达到证明目的.证明的过程中,由两个联立方程组结构的相似性运用了“同理可得”,整个证明过程也令人赏心悦目,感受到了逻辑证明与表达的顺畅、简约的美的魅力.
第(Ⅲ)问证明中用到了三点共线的充要条件,用到了过两点的直线的斜率公式,分别解出p,q以后,|OP|=|OQ|等价转化成了p= -q(或p+q=0.)此时分析前提条件(Ⅱ)及待证结论p= -q,关键在于沟通k1x1x2/(x1+x2)=k2x3x4/(x3+x4)与x1x4/(k1x1-k2x4)=-x2x3/(k1x2-k2x3)的联系.参考解答中的表述略去了一些变形的中间过程,使人不易看出沟通的线索,以及命题人变形的思路,因此读者理解起来感到困难.如果将两式做如下变形,则思路就显然顺畅自然.
设:k1x1x2/(x1+x2)=k2x3x4/(x3+x4)为①式,两边同取倒数,得
1/k1x2+1/k1x1=1/k2x4+1/k2x3 ①’
设:x1x4/(k1x1-k2x4)=-x2x3/(k1x2-k2x3)为 ②式,两边同取倒数,得k1/x4-k2/x1=k2/x2-k1/x3,移项得k2/x1+k2/x2=k1/x3+k1/x4 ②’
将①’两边同乘以k1·k2,即得
k2/x1+k2/x2=k1/x3+k1/x4
它与②’完全一样.这里利用两式同时变形的方法可以较容易实现目的,有分析、有综合,有思维,有运算.思路的选择有赖于对式子特征的观察联想.
综观这道题的题目特征及解答过程,我们看到了用代数方程但方法处理几何问题的作用与威力.
4.赏析:
上面我们看到,试题的结构及其解答都令人感到赏心悦目,至此,我们不禁要追问一句:试题是怎么命制出来的?它的背景是什么?它对我们的数学学习与教学、高三复习与备考有什么启示?
关于圆,有一个有趣的定理:
蝴蝶定理 设AB是圆O的弦,M是AB的中点.过M作圆O的两弦CD、EF,CF、DE分别交AB于H、G.则MH=MG.
这个定理画出来的几何图,很像一只翩翩飞舞的蝴蝶,所以叫做蝴蝶定理(图2).
盯着试题的图1仔细看,它像不像椭圆上翩翩飞舞的蝴蝶?
像,而且像极了.试题的证明过程及结果告诉我们,椭圆中蝴蝶定理依然成立,而且是用解析方法证明的.如果令椭圆的长轴,短轴相等,即a=b,则椭圆就变成了圆,椭圆中的蝴蝶定理就变成了圆上的蝴蝶定理,上面的证明一样适用.由于椭圆也可以看作将一个圆经“压缩变换”而得,故圆上的蝴蝶定理经“压缩变换”也可以变成椭圆上的蝴蝶定理.“翩翩蝴蝶舞椭圆,飞落高考数学花.”读者诸君欣赏至此,是否体会到了数学命题几何专家命制高考试题的“高招”及良苦用心?
[关于“椭圆上的蝴蝶”,张景中院士在其献给中学生的礼物一书《数学家的眼光》“巧思妙解”一节中有着精妙的论述,有兴趣的读者请参阅该书P54-59].
5.启示
椭圆上的蝴蝶翩翩飞舞,飞落到了北京数学高考试题的百花(草)园,令人欣喜异常.它虽然有着竞赛数学、仿射变换、数学名题的背景,然而这里证明它,却只用到了教科书里反复提到的三点共线问题和斜率公式,用到了解析几何最基本的方法.高级中学课本《平面解析几何》全一册(必修)数处提到三点共线问题,如P13习题一第14题:已知三点A(1,-1)、B(3,3)、C(4,5).求证:三点在一条直线上:P17练习4:证明:已知三点A、B、C,如果直线AB、AC的斜率相等,那么这三点在同一条直线上;P27习题二第9题:证明三点A(1,3)、B(5,7)、C(10,12)在同一条直线上;P47复习参考题一第3题:用两种方法证明:三点A(-2,12)、B(1,3)、C(4,-6)在同一条直线上.你看,课本上的练习、习题、复习参考题,反复提到了三点共线的证明,并且强调用不同的方法来证明.为什么?你(老师、学生)关注到了它吗?
实际上,三点共线的不同证明,可以把解析几何第一章的重点基础知识充分调动起来,组织起来.你可以用基本公式——平面上两点间的距离公式
证明|AC|=|AB∣+∣BC∣;你也可以应用定比分点公式x=(x1+λx2)/(1+λ),y=(y1+λy2)/(1+λ)去证λ=(x1-x)/(x-x2)=(y1-y)/(y-y2);你可以用过两点的直线的斜率公式Kp1p2=(y2-y1)/(x2-x1),去证KAB=KAC;你还可以先建立直线AB的方程f(x,y)=0,然后验证点C的坐标适合直线AB的方程即f(x,y)=0;你也可以在建立直线AB的方程之后,利用点到直线的距离公式
证明dc-AB=0;你还可以计算△ABC的面积,去证S△ABC=0.你看,有五、六种方法可以解决同一个问题,当然难度有高有低.一题多解中选择方法、优化方法也是能力(洞察、观察)的体现,从比较中才可以鉴别方法的优劣.据说考试下来,有一些重点中学的尖子生对自己没能解答出第(Ⅲ)问很懊悔,一些老师也说这个题目“运算量太大难以完成”!不知读者诸君欣赏至此,能不能发现上述问题的症结究竟发生在哪里?北京市有许多重点中学的师生,对高中数学课本的习题不屑一顾,很少去钻研教材中的例题、习题,去寻求与发现知识之间的内在联系,去总结解题的原则、思路与规律.各种各样的复习资料,几十套几十套的各地模拟试卷,使高三学生跳进题海做得昏天黑地而难以自拔,这哪里还谈得上素质教育与培养能力?我们应当从欣赏“翩翩飞舞的椭圆蝴蝶”中去用心体会“精选题目充分利用题目的“营养”价值”在数学教学与复习中的重要作用,从而解放思想,勇敢大胆地摒弃“题海战术”.而要使学生跳出题海,老师就必须首先跳入题海,“题海探珠”,感悟数学教育改革的真谛.——注重基础、注重理解、注重联系、注重能力.
国际水平现在大大提高,我们的判断方式也有所改变,生活只要你留心观察,就会有很大的收获!1年前查看全部
大家在问
- 1人类的惯用右手和惯用左手是一对相对性状.基因类型AA,Aa的个体惯用右手,而aa的个体惯用左手,一个惯用右手(杂合体)的
- 2翻译 Beijing is a city for all seasons. You can alw
- 3为什么越位于金属活动顺序后面的金属,越不容易得电子,氧化性越强.
- 4可以帮忙构思一篇作文吗?关于“三比三不比“的,从中挑选一题材进行写作!
- 5收住说话的声音,连大气也不敢出(根据意思说词语)
- 6天上为什么只有那一颗星星最亮?
- 7粗糙、摧毁、原谅、竣工、陡峭、模糊、慌张、缓慢、寸草不生、波涛汹涌的反义词
- 8如图,一轮船由南向北航行到O处时,发现与轮船相距40海里的A岛在北偏东33°方向.已知A岛周围20海里水域有暗礁,如果不
- 9在人群中,生来就惯用右手一生来就惯用左手(不包括后天的矫正和练习)是一对相对性状.父亲惯用左手,母亲惯用右手,他们生的孩
- 10我塑料杯倒开水进去泡茶 有一层白色泡泡出现 过了一会有没了 = = 杯子是豪丰家品 塑料的400ml茶水杯
- 11While talking about his own happy childhood,_______ on his f
- 12求一道化学计算题,尿素是一种肥效高的常用氮肥,其化学式为CO(NH2)2.现有一种尿素样品,测得氮元素的质量分数为43.
- 13我们也是朋友 600字的 我们也是朋友 不用文章 只要给我写作的思路 开头怎么写 就OK了
- 141.-Are you good at dancing,Maria?
- 15请伸出右手,观察您的手指,会发现手指会有轻微地抖动(心情稳定,身体健康),为什么呢?