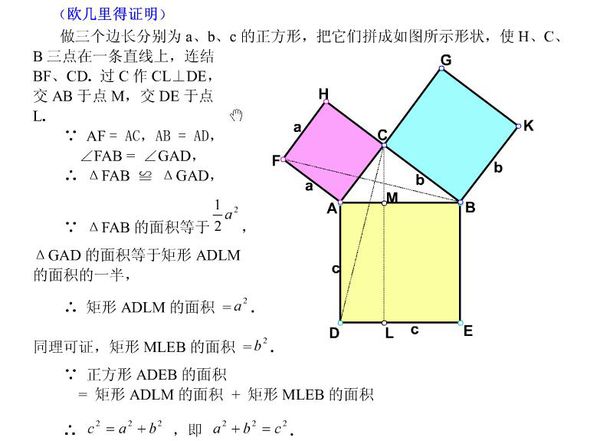
欧几里得在《几何原本》指出“当一个数是另一个数的某一部分或某几部分”.
 wwwwzhangy2022-10-04 11:39:541条回答
wwwwzhangy2022-10-04 11:39:541条回答
已提交,审核后显示!提交回复
共1条回复
 jean55555 共回答了16个问题
jean55555 共回答了16个问题 |采纳率93.8%- 是他的几倍或几分之几
希望能够帮助你 - 1年前
相关推荐
- 一个拓扑概念求解答欧几里得空间里设X={1,2,3}.则{X,{},{1,2}}是X的一个拓扑,但{X,{},{1},{
一个拓扑概念求解答
欧几里得空间里
设X={1,2,3}.则{X,{},{1,2}}是X的一个拓扑,但{X,{},{1},{2}}不是拓扑.
这是为什么 微笑旋风1年前1
微笑旋风1年前1 -
 slowly1971 共回答了16个问题
slowly1971 共回答了16个问题 |采纳率93.8%因为{1}∪{2}={1,2}不属于拓扑T
故{X,{},{1},{2}}不是拓扑1年前查看全部
- 三角形内角和等于180°,这是古希腊数学家欧几里得提出的定理,人们一直把它当作任何条件下都适用的真理。但19世纪初俄国数
三角形内角和等于180°,这是古希腊数学家欧几里得提出的定理,人们一直把它当作任何条件下都适用的真理。但19世纪初俄国数学家罗巴切夫斯基提出:在凹曲面上,三角形内角和小于180°;随后,德国数学家黎曼提出:在球形凸面上,三角形内角和大于180°。这个事例说明( )
A.真理是客观的 B.真理与谬误分不清楚 C.真理是有条件的 D.真理都是具体的  bfghfrjgr1年前1
bfghfrjgr1年前1 -
 神祭 共回答了19个问题
神祭 共回答了19个问题 |采纳率89.5%C
材料提到“人们一直把它当作任何条件下都适用的真理”,当后来条件改变,这个定理就不适用了,说明真理是有条件的。1年前查看全部
- 谁能告诉我欧几里得的《几何原本》里的23个定义,5条公设,5条公理?
谁能告诉我欧几里得的《几何原本》里的23个定义,5条公设,5条公理?
欧氏几何原本里的公理?公式?
附加定义?
 雨夜陌路人1年前1
雨夜陌路人1年前1 -
 即时飘 共回答了19个问题
即时飘 共回答了19个问题 |采纳率84.2%http://forum.heftyedu.com/viewthread.php?tid=730这是个论坛不过可以不用注册就能下载,除了几何原本还有别的数学图书1年前查看全部
- 欧几里得证明的勾股定理
 richmark1年前1
richmark1年前1 -
 流樱 共回答了20个问题
流樱 共回答了20个问题 |采纳率90%1年前查看全部
- 古希腊数学家欧几里得提出了三角形内角和等于180°的定理。到了19世纪初,俄国数学家罗巴切夫斯基提出:在凹曲面上,三角形
古希腊数学家欧几里得提出了三角形内角和等于180°的定理。到了19世纪初,俄国数学家罗巴切夫斯基提出:在凹曲面上,三角形内角之和小于180°。随后德国数学家黎曼提出:在球形凸面上,三角形内角之和大于180°。上述材料体现了 [ ]①欧几里得定理不再是真理 ②真理有自己适用的条件和范围,真理是有条件的 ③真理是主观与客观、理论与实践的具体的历史的统一 ④不顾条件的变化,真理会转化为谬误
A、①②③
B、②③
C、②③④
D、③④ 好的a1年前1
好的a1年前1 -
 sweetnssslife 共回答了28个问题
sweetnssslife 共回答了28个问题 |采纳率96.4%B1年前查看全部
- 欧几里得的几何原本是公理化思想的萌芽,这句话对吗
 rsgrhj1年前1
rsgrhj1年前1 -
 单身的xx 共回答了19个问题
单身的xx 共回答了19个问题 |采纳率94.7%是的.欧氏几何的五条公理是系统地研究平面几何理论的开端,而在希尔伯特时代,公理化理论得到快速发展.而这种发展,主要体现在对欧氏几何五条公理的补充和完善上.
所以说,欧氏几何是公理化思想的萌芽,这种说法是正确的.1年前查看全部
- 为什么欧几里得距离在高维空间没有意义?
为什么欧几里得距离在高维空间没有意义?
我好像说得不清楚.这么说吧:
X1=(X11,X12,X13,X14,.X1n,.)
X2=(X21,X22,X23,X24,.X2n,.)
S(X1,X2,n)=(sigma((X1i-X2i)^2))^(1/2) i=1,2,...n
当n趋于无穷时,这算不算高维度空间欧几里得距离呢?
当X1,X2,X3互不相同,且n趋于无穷时,对任意e>0,
恒有limp(S(X1,X2,n)/S(X1,X3,n)-1 rain_e171年前1
rain_e171年前1 -
 stsnake 共回答了19个问题
stsnake 共回答了19个问题 |采纳率100%因为欧几里得空间与所谓的高维度空间是两个不同的概念,所以他们中的距离定义也是不同的,就像在立体几何中是两点间直线距离最短,而在球面几何中则是经过两点的弧线最短1年前查看全部
- 英语翻译请把以下单词翻译成英文1“落伍” 2“走弯路” 3“万有引力定律” 4“牛顿力学定律” 5“欧几里得定理” 6
英语翻译
请把以下单词翻译成英文
1“落伍” 2“走弯路” 3“万有引力定律” 4“牛顿力学定律”
5“欧几里得定理” 6 “非欧几里得定理“ 7 “智慧结晶”
8“挑战极限” 9“奔驰(车牌)” 10“宝马(车牌)”
11“夏利(车牌)” 12“香奈儿” 13“福尔摩斯侦探小说”
14“科幻小说” 15“寓言故事” 16“侦探小说” 17“发展特长”
18“遗传育种” 19“杂交水稻” 20“转基因大豆” 21“基因改良”
22“漫画书” roro01251年前2
roro01251年前2 -
 yingyi215 共回答了16个问题
yingyi215 共回答了16个问题 |采纳率106.3%1"backward" 2 "make detours" 3 "the law of gravity" 4 "Newton's mechanics's Law"
5 "Euclid theorem" 6 "non-Euclid theorem" 7 "crystallization of the wisdom"
8 "ultimate challenge" 9 "Mercedes (license plate)" 10 "BMW (plates)"
11 "Xiali (plates)" 12 "Chanel" 13 "Holmes detective novels"
14 "science fiction" 15 "fable" 16 "detective novels" 17 "developing expertise"
18 "breeding" 19 "hybrid rice" 20 "transgenic soybeans" 21 "genetically modified"
22 "comic book"1年前查看全部
- 求一句欧几里得的《几何原本》关于平面角的原文和英文原文
求一句欧几里得的《几何原本》关于平面角的原文和英文原文
求
第一卷
定义
8.平面角是在一平面内但不在一条直线上的两条相交线相互的倾斜度
这句的原文和英文原文
谢谢
我是想要原著上的原文 不是帮我翻译 谢谢 taotian1231年前3
taotian1231年前3 -
 573211234 共回答了16个问题
573211234 共回答了16个问题 |采纳率93.8%There was no royal road to geometry.
原文是
Ptolemy I,king of Egypt,asked Euclid "if there was in geometry any shorter way than that of the Elements",and he answered that there was no royal road to geometry.1年前查看全部
- 几何原本欧几里得《几何原本》这本书里主要有什么几何的内容里面有没有解析几何,立体几何,向量。没有的话,那还有什么书里有。
 茅台文化1年前3
茅台文化1年前3 -
 pscwwang 共回答了15个问题
pscwwang 共回答了15个问题 |采纳率93.3%没有向量的1年前查看全部
- 再看《哥德尔逻辑的困境》一书时 第27页提及所有整数都小于某些素数 并称之为欧几里得的定理 求证
 义非1年前1
义非1年前1 -
 勐海普洱茶 共回答了19个问题
勐海普洱茶 共回答了19个问题 |采纳率84.2%这个结论就是素数有无穷多.
欧几里得的证明是用反证法.
假设素数只有有限个,设它们为p1,p2,p3,...,pn.
考虑N = p1·p2·p3·...·pn+1,则N不被p1,p2,p3,...,pn中的任何一个整除.
N要么本身就是素数,要么含有p1,p2,p3,...,pn之外的素因子,矛盾.1年前查看全部
- 欧几里德数学的一个问题欧几里得证明了:一个偶数是完美数,当且仅当它具有如下形式:2p-1(2p-1) 其中2p-1是素数
欧几里德数学的一个问题
欧几里得证明了:一个偶数是完美数,当且仅当它具有如下形式:2p-1(2p-1) 其中2p-1是素数.
“2p-1(2p-1) ”中有没有丢失什么符号?真正形式是什么? shjclj1年前1
shjclj1年前1 -
 asdf_858 共回答了17个问题
asdf_858 共回答了17个问题 |采纳率76.5%2p-1(2p-1)的实际意义是:2的P-1次方乘以2的P次方减1的差 其中2的P次方减1的差是素数1年前查看全部
- 信息论为什么是正确的?我认为数学或者科学必须有一个坚实的基础,比如说欧几里得的《几何原本》的基础就是二十多条公理,这些公
信息论为什么是正确的?
我认为数学或者科学必须有一个坚实的基础,比如说欧几里得的《几何原本》的基础就是二十多条公理,这些公理连3岁小孩都很容易理解(比如平行线不会相交,整体大于部分等),再比如牛顿的力学体系,其基础是牛顿三定律,可以通过试验的方式证明其正确.
信息论的基础是信息量,及I(a)=-log p(a),为什么其是正确的?为什么不能把其定义为I(a)=-log p(a)+10或者I(a)=1/ p(a) 呢?
如果说不清楚可以给一个链接或者是一本书的某几页,我自己去查 紫衣天使1年前2
紫衣天使1年前2 -
 zhu-atom 共回答了27个问题
zhu-atom 共回答了27个问题 |采纳率92.6%可以自己定义的,但是必须满足几个条件,具体可以查看Wikipedia.
NN的,度娘老说我包含不能发表的东西
本来我敲了大段字,度娘老是说我包含不能发表的,于是删减成这样了.后面就没了,不高兴敲了呵呵
给个链接,你自己去看吧,多看些英文的对自己很有帮助的,千万别看中文版的
以及1年前查看全部
- 一条线段用尺规分3段,5段仅仅用尺规,就是欧几里得的要求尺是没有刻度的我知道怎么分偶数等份,
 细脚伶仃1年前2
细脚伶仃1年前2 -
 榷27 共回答了19个问题
榷27 共回答了19个问题 |采纳率84.2%从线段的一点做一个任意不为0的角度的一条射线,用圆规将射线的一段3,5等分,连接线段的另一端点,做平行线,可得3,5等分1年前查看全部
- 麻烦老师解答:欧几里得的主要成就是
麻烦老师解答:欧几里得的主要成就是
欧几里得的主要成就是 [ ] A.找到计算圆周率的科学计算方法
B.提出物体体积的计算
C.提出杠杆原理
D.总结前人成果写出《几何原本》 bagayalujiji1年前1
bagayalujiji1年前1 -
 乱跳舞 共回答了24个问题
乱跳舞 共回答了24个问题 |采纳率87.5%D1年前查看全部
- 欧几里得原理(辗转相除法)其中有以下定理:
欧几里得原理(辗转相除法)其中有以下定理:
定理四 若a|bc,(a,b)=1,则a|c.
以下为定理的连接: soclean1年前4
soclean1年前4 -
 cjiayoung 共回答了20个问题
cjiayoung 共回答了20个问题 |采纳率80%若a|bc,(a,b)=1,则a|c
翻译:若整数a能整除b、c的乘积,且a、b的最大公约数是1,则a能整除c.
这个“|”是“整除”的意思.(除数在前,被除数在后)1年前查看全部
- 关于欧几里得几何原本的第一个命题
关于欧几里得几何原本的第一个命题
在证明第一个命题:由已知线段可作一个等边三角形时,欧几里得过已知线段的端点A、B分别作了一个圆,然后他就直接说两圆交与C点,可是从前面的公理、公设以及定义中无法直接看出这两个圆有交点,请问如何证明此交点的存在性? ptxwx1年前1
ptxwx1年前1 -
 orangeboy1 共回答了13个问题
orangeboy1 共回答了13个问题 |采纳率100%定义
圆与圆的位置关系的定义R≥r
外离 d>R+r
外切d=R+r
相交R-1年前查看全部
- 勾股定理欧几里得证法
 手芯V手背1年前1
手芯V手背1年前1 -
 8060575 共回答了15个问题
8060575 共回答了15个问题 |采纳率86.7%如果两个三角形有两组对应边和这两组边所夹的角相等,则两三角形全等.(SAS定理) 三角形面积是任一同底同高之平行四边形面积的一半.任意一个正方形的面积等于其二边长的乘积.任意一个四方形的面积等于其二边长的乘积(据辅助定理3).证明的概念为:把上方的两个正方形转换成两个同等面积的平行四边形,再旋转并转换成下方的两个同等面积的长方形.
其证明如下:
设△ABC为一直角三角形,其直角为CAB.其边为BC、AB、和CA,依序绘成四方形CBDE、BAGF和ACIH.画出过点A之BD、CE的平行线.此线将分别与BC和DE直角相交于K、L.分别连接CF、AD,形成两个三角形BCF、BDA.∠CAB和∠BAG都是直角,因此C、A 和 G 都是线性对应的,同理可证B、A和H.∠CBD和∠FBA皆为直角,所以∠ABD等于∠FBC.因为 AB 和 BD 分别等于 FB 和 BC,所以△ABD 必须相等于△FBC.因为 A 与 K 和 L是线性对应的,所以四方形 BDLK 必须二倍面积于△ABD.因为C、A和G有共同线性,所以正方形BAGF必须二倍面积于△FBC.因此四边形 BDLK 必须有相同的面积 BAGF = AB².同理可证,四边形 CKLE 必须有相同的面积 ACIH = AC².把这两个结果相加,AB²+ AC² = BD×BK + KL×KC 由于BD=KL,BD×BK + KL×KC = BD(BK + KC) = BD×BC 由于CBDE是个正方形,因此AB² + AC² = C².此证明是于欧几里得《几何原本》一书第1.47节所提出的1年前查看全部
- 三角形内角之和等于180度,这是古希腊数学家欧几里得提出的定理。在此之后的两千多年里,人们一直把它当作任何条件下都适用的
三角形内角之和等于180度,这是古希腊数学家欧几里得提出的定理。在此之后的两千多年里,人们一直把它当作任何条件下都适用的真理。但是,19世纪初,俄国数学家罗巴切夫斯基提出:在凹曲面上,三角形内角之和小于180度。随后,德国数学家黎曼提出:在球形凸面上,三角形内角之和大于180度。这说明真理是 [ ]①因人而异的 ②具体的 ③有条件的 ④客观的
A.①②
B.①③
C.①④
D.②③ 82k5ah1年前1
82k5ah1年前1 -
 南海古榕 共回答了24个问题
南海古榕 共回答了24个问题 |采纳率95.8%D1年前查看全部
- 明末徐光启仰慕西方自然科学,与意大利传教士利玛窦合作翻译出版了希腊数学家欧几里得的《几何原本》;鉴于数学应用的广泛性,他
明末徐光启仰慕西方自然科学,与意大利传教士利玛窦合作翻译出版了希腊数学家欧几里得的《几何原本》;鉴于数学应用的广泛性,他还建议开展分科研究。这主要反映了
a.西方教会势力开始侵入*** b.徐光启思想的创新性和先进性 c.***士人开始有了民族危机意识 d.***的传统科技进入了顶峰时期  anletitbe1年前1
anletitbe1年前1 -
 小龙白 共回答了21个问题
小龙白 共回答了21个问题 |采纳率90.5%B
1年前查看全部
- (2010•深圳一模)图中的程序框图所描述的算法称为欧几里得辗转相除法.若输入m=2010,n=1541,则输出m=__
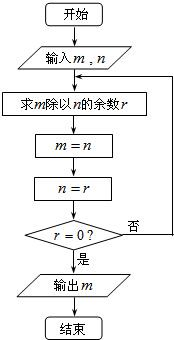 (2010•深圳一模)图中的程序框图所描述的算法称为欧几里得辗转相除法.若输入m=2010,n=1541,则输出m=______.(注:框图中的赋值符号“=”也可以写成“←”或“:=”)
(2010•深圳一模)图中的程序框图所描述的算法称为欧几里得辗转相除法.若输入m=2010,n=1541,则输出m=______.(注:框图中的赋值符号“=”也可以写成“←”或“:=”)  为何黎明1年前1
为何黎明1年前1 -
 yu3rar 共回答了26个问题
yu3rar 共回答了26个问题 |采纳率84.6%解题思路:先求出m除以n的余数,然后利用辗转相除法,将n的值赋给m,将余数赋给n,进行迭代,一直算到余数为零时m的值即可.当m=2010,n=1541,m除以n的余数是469
此时m=1541,n=469,m除以n的余数是134
此时m=469,n=134,m除以n的余数是67
此时m=134,n=67,m除以n的余数是0,
此时m=67,n=0
退出程序,输出结果为67
故答案为67点评:
本题考点: 程序框图.
考点点评: 算法和程序框图是新课标新增的内容,在近两年的新课标地区高考都考查到了,这启示我们要给予高度重视,属于基础题.1年前查看全部
- 古希腊数学家欧几里得证明了素数是无限的,请问如何证明的?回答最好能简明易懂,
 狼外婆991年前4
狼外婆991年前4 -
 bizhi2 共回答了17个问题
bizhi2 共回答了17个问题 |采纳率94.1%假设素数个数有限,则必有一个最大的
设最大的素数是P
令n=2*3*5*7*……*P+1
即把所有的素数相乘并加上1
显然n>P
若因为P是最大素数,所以n是合数
则n能被2,3,……,P中至少一个素数整除
但用这些数去除n,都有余数1,即都不能整除
这就有两种可能
(1),n是素数
(2),n是合数,但他只能被大于P的素数整除
这两种情况都和P是最大素数矛盾.
所以假设错误
所以素数是无限1年前查看全部
- 用欧几里得工具,将一线段任意等分是件简单的事;也许古希腊人在求解类似的任意等分角的问题时,提出了三等分角问题;也许(更有
用欧几里得工具,将一线段任意等分是件简单的事;也许古希腊人在求解类似的任意等分角的问题时,提出了三等分角问题;也许(更有可能)这问题是在作正九边形时产生的,在那里,要三等分一个60°角.在研究三等分角问题时,看来希腊人首先把它们归结成所谓斜向...
 walk-in-the-rain1年前1
walk-in-the-rain1年前1 -
 zxgsb 共回答了16个问题
zxgsb 共回答了16个问题 |采纳率93.8%我感觉是这样的把它看成一个等边三角形 然后在其中一边3等分 这样不就可以把60度角三等分吗是这样吗不行的话 加我QQ 不懂的数学问题继续问1年前查看全部
- 它是地中海地区最大的城市,也是地中海地区和东方各国贸易与文化交流的中心,著名科学家欧几里得在这里取得学术成就,"
它是地中海地区最大的城市,也是地中海地区和东方各国贸易与文化交流的中心,著名科学家欧几里得在这里取得学术成就,"它"是?
 洞庭湖田鼠1年前7
洞庭湖田鼠1年前7 -
 青青露水 共回答了5个问题
青青露水 共回答了5个问题 |采纳率40%应该是雅典1年前查看全部
- 希腊数学家欧几里得 对勾股定理的证明方法
希腊数学家欧几里得 对勾股定理的证明方法
是对毕达哥拉斯失传方法的一个很好的证明
快点,在线等哦
需要几何图形 zenlijun1年前2
zenlijun1年前2 -
 持久以恒 共回答了17个问题
持久以恒 共回答了17个问题 |采纳率88.2%http://bbs.eduol.cn/printpage.asp?BoardID=39&ID=171933
魅力无比的定理证明
——勾股定理的证明
勾股定理是几何学中的明珠,所以它充满魅力,千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者,有普通的老百姓,也有尊贵的政要权贵,甚至有国家总统。也许是因为勾股定理既重要又简单,更容易吸引人,才使它成百次地反复被人炒作,反复被人论证。1940年出版过一本名为《毕达哥拉斯命题》的勾股定理的证明专辑,其中收集了367种不同的证明方法。实际上还不止于此,有资料表明,关于勾股定理的证明方法已有500余种,仅我国清末数学家华蘅芳就提供了二十多种精彩的证法。这是任何定理无法比拟的。
在这数百种证明方法中,有的十分精彩,有的十分简洁,有的因为证明者身份的特殊而非常著名。
首先介绍勾股定理的两个最为精彩的证明,据说分别来源于中国和希腊。
1.中国方法
画两个边长为(a+b)的正方形,如图,其中a、b为直角边,c为斜边。这两个正方形全等,故面积相等。
左图与右图各有四个与原直角三角形全等的三角形,左右四个三角形面积之和必相等。从左右两图中都把四个三角形去掉,图形剩下部分的面积必相等。左图剩下两个正方形,分别以a、b为边。右图剩下以c为边的正方形。于是
a2+b2=c2。
这就是我们几何教科书中所介绍的方法。既直观又简单,任何人都看得懂。
2.希腊方法
直接在直角三角形三边上画正方形,如图。
容易看出,
△ABA’ ≌△AA’’ C。
过C向A’’B’’引垂线,交AB于C’,交A’’B’’于C’’。
△ABA’与正方形ACDA’同底等高,前者面积为后者面积的一半,△AA’’C与矩形AA’’C’’C’同底等高,前者的面积也是后者的一半。由△ABA’≌△AA’’C,知正方形ACDA’的面积等于矩形AA’’C’’C’的面积。同理可得正方形BB’EC的面积等于矩形B’’BC’C’’的面积。
于是,
S正方形AA’’B’’B=S正方形ACDA’+S正方形BB’EC,
即 a2+b2=c2。
至于三角形面积是同底等高的矩形面积之半,则可用割补法得到(请读者自己证明)。这里只用到简单的面积关系,不涉及三角形和矩形的面积公式。
这就是希腊古代数学家欧几里得在其《几何原本》中的证法。
以上两个证明方法之所以精彩,是它们所用到的定理少,都只用到面积的两个基本观念:
⑴ 全等形的面积相等;
⑵ 一个图形分割成几部分,各部分面积之和等于原图形的面积。
这是完全可以接受的朴素观念,任何人都能理解。
我国历代数学家关于勾股定理的论证方法有多种,为勾股定理作的图注也不少,其中较早的是赵爽(即赵君卿)在他附于《周髀算经》之中的论文《勾股圆方图注》中的证明。采用的是割补法:
如图,将图中的四个直角三角形涂上朱色,把中间小正方形涂上黄色,叫做中黄实,以弦为边的正方形称为弦实,然后经过拼补搭配,“令出入相补,各从其类”,他肯定了勾股弦三者的关系是符合勾股定理的。即“勾股各自乘,并之为弦实,开方除之,即弦也”。
赵爽对勾股定理的证明,显示了我国数学家高超的证题思想,较为简明、直观。
西方也有很多学者研究了勾股定理,给出了很多证明方法,其中有文字记载的最早的证明是毕达哥拉斯给出的。据说当他证明了勾股定理以后,欣喜若狂,杀牛百头,以示庆贺。故西方亦称勾股定理为“百牛定理”。遗憾的是,毕达哥拉斯的证明方法早已失传,我们无从知道他的证法。
下面介绍的是美国第二十任总统伽菲尔德对勾股定理的证明。
如图,
S梯形ABCD= (a+b)2
= (a2+2ab+b2), ①
又S梯形ABCD=S△AED+S△EBC+S△CED
= ab+ ba+ c2
= (2ab+c2)。 ②
比较以上二式,便得
a2+b2=c2。
这一证明由于用了梯形面积公式和三角形面积公式,从而使证明相当简洁。
1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证明。5年后,伽菲尔德就任美国第二十任总统。后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为勾股定理的“总统”证法,这在数学史上被传为佳话。
在学习了相似三角形以后,我们知道在直角三角形中,斜边上的高把这个直角三角形所分成的两个直角三角形与原三角形相似。
如图,Rt△ABC中,∠ACB=90°。作CD⊥BC,垂足为D。则
△BCD∽△BAC,△CAD∽△BAC。
由△BCD∽△BAC可得BC2=BD ? BA, ①
由△CAD∽△BAC可得AC2=AD ? AB。 ②
我们发现,把①、②两式相加可得
BC2+AC2=AB(AD+BD),
而AD+BD=AB,
因此有 BC2+AC2=AB2,这就是
a2+b2=c2。
这也是一种证明勾股定理的方法,而且也很简洁。它利用了相似三角形的知识。
在对勾股定理为数众多的证明中,人们也会犯一些错误。如有人给出了如下证明勾股定理的方法:
设△ABC中,∠C=90°,由余弦定理
c2=a2+b2-2abcosC,
因为∠C=90°,所以cosC=0。所以
a2+b2=c2。
这一证法,看来正确,而且简单,实际上却犯了循环证论的错误。原因是余弦定理的证明来自勾股定理。
人们对勾股定理感兴趣的原因还在于它可以作推广。
欧几里得在他的《几何原本》中给出了勾股定理的推广定理:“直角三角形斜边上的一个直边形,其面积为两直角边上两个与之相似的直边形面积之和”。
从上面这一定理可以推出下面的定理:“以直角三角形的三边为直径作圆,则以斜边为直径所作圆的面积等于以两直角边为直径所作两圆的面积和”。
勾股定理还可以推广到空间:以直角三角形的三边为对应棱作相似多面体,则斜边上的多面体的表面积等于直角边上两个多面体表面积之和。
若以直角三角形的三边为直径分别作球,则斜边上的球的表面积等于两直角边上所作二球表面积之和。
如此等等。
【附录】
一、【《周髀算经》简介】
《周髀算经》算经十书之一。约成书于公元前二世纪,原名《周髀》,它是我国最古老的天文学著作,主要阐明当时的盖天说和四分历法。唐初规定它为国子监明算科的教材之一,故改名《周髀算经》。《周髀算经》在数学上的主要成就是介绍了勾股定理及其在测量上的应用。原书没有对勾股定理进行证明,其证明是三国时东吴人赵爽在《周髀注》一书的《勾股圆方图注》中给出的。
《周髀算经》使用了相当繁复的分数算法和开平方法。
二、【伽菲尔德证明勾股定理的故事】
1876年一个周末的傍晚,在美国首都华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员伽菲尔德。他走着走着,突然发现附近的一个小石凳上,有两个小孩正在聚精会神地谈论着什么,时而大声争论,时而小声探讨。由于好奇心驱使,伽菲尔德循声向两个小孩走去,想搞清楚两个小孩到底在干什么。只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形。于是伽菲尔德便问他们在干什么?那个小男孩头也不抬地说:“请问先生,如果直角三角形的两条直角边分别为3和4,那么斜边长为多少呢?”伽菲尔德答道:“是5呀。”小男孩又问道:“如果两条直角边长分别为5和7,那么这个直角三角形的斜边长又是多少?”伽菲尔德不假思索地回答道:“那斜边的平方一定等于5的平方加上7的平方。”小男孩又说:“先生,你能说出其中的道理吗?”伽菲尔德一时语塞,无法解释了,心里很不是滋味。
于是,伽菲尔德不再散步,立即回家,潜心探讨小男孩给他出的难题。他经过反复思考与演算,终于弄清了其中的道理,并给出了简洁的证明方法。
转引自:http://tw.ntu.edu.cn/education/yanjiu/中“数学的发现”栏目。图无法转贴,请查看原文。
魅力无比的定理证明
——勾股定理的证明
勾股定理是几何学中的明珠,所以它充满魅力,千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者,有普通的老百姓,也有尊贵的政要权贵,甚至有国家总统。也许是因为勾股定理既重要又简单,更容易吸引人,才使它成百次地反复被人炒作,反复被人论证。1940年出版过一本名为《毕达哥拉斯命题》的勾股定理的证明专辑,其中收集了367种不同的证明方法。实际上还不止于此,有资料表明,关于勾股定理的证明方法已有500余种,仅我国清末数学家华蘅芳就提供了二十多种精彩的证法。这是任何定理无法比拟的。
在这数百种证明方法中,有的十分精彩,有的十分简洁,有的因为证明者身份的特殊而非常著名。
首先介绍勾股定理的两个最为精彩的证明,据说分别来源于中国和希腊。
1.中国方法
画两个边长为(a+b)的正方形,如图,其中a、b为直角边,c为斜边。这两个正方形全等,故面积相等。
左图与右图各有四个与原直角三角形全等的三角形,左右四个三角形面积之和必相等。从左右两图中都把四个三角形去掉,图形剩下部分的面积必相等。左图剩下两个正方形,分别以a、b为边。右图剩下以c为边的正方形。于是
a2+b2=c2。
这就是我们几何教科书中所介绍的方法。既直观又简单,任何人都看得懂。
2.希腊方法
直接在直角三角形三边上画正方形,如图。
容易看出,
△ABA’ ≌△AA’’ C。
过C向A’’B’’引垂线,交AB于C’,交A’’B’’于C’’。
△ABA’与正方形ACDA’同底等高,前者面积为后者面积的一半,△AA’’C与矩形AA’’C’’C’同底等高,前者的面积也是后者的一半。由△ABA’≌△AA’’C,知正方形ACDA’的面积等于矩形AA’’C’’C’的面积。同理可得正方形BB’EC的面积等于矩形B’’BC’C’’的面积。
于是,
S正方形AA’’B’’B=S正方形ACDA’+S正方形BB’EC,
即 a2+b2=c2。
至于三角形面积是同底等高的矩形面积之半,则可用割补法得到(请读者自己证明)。这里只用到简单的面积关系,不涉及三角形和矩形的面积公式。
这就是希腊古代数学家欧几里得在其《几何原本》中的证法。
以上两个证明方法之所以精彩,是它们所用到的定理少,都只用到面积的两个基本观念:
⑴ 全等形的面积相等;
⑵ 一个图形分割成几部分,各部分面积之和等于原图形的面积。
这是完全可以接受的朴素观念,任何人都能理解。
我国历代数学家关于勾股定理的论证方法有多种,为勾股定理作的图注也不少,其中较早的是赵爽(即赵君卿)在他附于《周髀算经》之中的论文《勾股圆方图注》中的证明。采用的是割补法:
如图,将图中的四个直角三角形涂上朱色,把中间小正方形涂上黄色,叫做中黄实,以弦为边的正方形称为弦实,然后经过拼补搭配,“令出入相补,各从其类”,他肯定了勾股弦三者的关系是符合勾股定理的。即“勾股各自乘,并之为弦实,开方除之,即弦也”。
赵爽对勾股定理的证明,显示了我国数学家高超的证题思想,较为简明、直观。
西方也有很多学者研究了勾股定理,给出了很多证明方法,其中有文字记载的最早的证明是毕达哥拉斯给出的。据说当他证明了勾股定理以后,欣喜若狂,杀牛百头,以示庆贺。故西方亦称勾股定理为“百牛定理”。遗憾的是,毕达哥拉斯的证明方法早已失传,我们无从知道他的证法。
下面介绍的是美国第二十任总统伽菲尔德对勾股定理的证明。
如图,
S梯形ABCD= (a+b)2
= (a2+2ab+b2), ①
又S梯形ABCD=S△AED+S△EBC+S△CED
= ab+ ba+ c2
= (2ab+c2)。 ②
比较以上二式,便得
a2+b2=c2。
这一证明由于用了梯形面积公式和三角形面积公式,从而使证明相当简洁。
1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证明。5年后,伽菲尔德就任美国第二十任总统。后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为勾股定理的“总统”证法,这在数学史上被传为佳话。
在学习了相似三角形以后,我们知道在直角三角形中,斜边上的高把这个直角三角形所分成的两个直角三角形与原三角形相似。
如图,Rt△ABC中,∠ACB=90°。作CD⊥BC,垂足为D。则
△BCD∽△BAC,△CAD∽△BAC。
由△BCD∽△BAC可得BC2=BD ? BA, ①
由△CAD∽△BAC可得AC2=AD ? AB。 ②
我们发现,把①、②两式相加可得
BC2+AC2=AB(AD+BD),
而AD+BD=AB,
因此有 BC2+AC2=AB2,这就是
a2+b2=c2。
这也是一种证明勾股定理的方法,而且也很简洁。它利用了相似三角形的知识。
在对勾股定理为数众多的证明中,人们也会犯一些错误。如有人给出了如下证明勾股定理的方法:
设△ABC中,∠C=90°,由余弦定理
c2=a2+b2-2abcosC,
因为∠C=90°,所以cosC=0。所以
a2+b2=c2。
这一证法,看来正确,而且简单,实际上却犯了循环证论的错误。原因是余弦定理的证明来自勾股定理。
人们对勾股定理感兴趣的原因还在于它可以作推广。
欧几里得在他的《几何原本》中给出了勾股定理的推广定理:“直角三角形斜边上的一个直边形,其面积为两直角边上两个与之相似的直边形面积之和”。
从上面这一定理可以推出下面的定理:“以直角三角形的三边为直径作圆,则以斜边为直径所作圆的面积等于以两直角边为直径所作两圆的面积和”。
勾股定理还可以推广到空间:以直角三角形的三边为对应棱作相似多面体,则斜边上的多面体的表面积等于直角边上两个多面体表面积之和。
若以直角三角形的三边为直径分别作球,则斜边上的球的表面积等于两直角边上所作二球表面积之和。
如此等等。
【附录】
一、【《周髀算经》简介】
《周髀算经》算经十书之一。约成书于公元前二世纪,原名《周髀》,它是我国最古老的天文学著作,主要阐明当时的盖天说和四分历法。唐初规定它为国子监明算科的教材之一,故改名《周髀算经》。《周髀算经》在数学上的主要成就是介绍了勾股定理及其在测量上的应用。原书没有对勾股定理进行证明,其证明是三国时东吴人赵爽在《周髀注》一书的《勾股圆方图注》中给出的。
《周髀算经》使用了相当繁复的分数算法和开平方法。
二、【伽菲尔德证明勾股定理的故事】
1876年一个周末的傍晚,在美国首都华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员伽菲尔德。他走着走着,突然发现附近的一个小石凳上,有两个小孩正在聚精会神地谈论着什么,时而大声争论,时而小声探讨。由于好奇心驱使,伽菲尔德循声向两个小孩走去,想搞清楚两个小孩到底在干什么。只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形。于是伽菲尔德便问他们在干什么?那个小男孩头也不抬地说:“请问先生,如果直角三角形的两条直角边分别为3和4,那么斜边长为多少呢?”伽菲尔德答道:“是5呀。”小男孩又问道:“如果两条直角边长分别为5和7,那么这个直角三角形的斜边长又是多少?”伽菲尔德不假思索地回答道:“那斜边的平方一定等于5的平方加上7的平方。”小男孩又说:“先生,你能说出其中的道理吗?”伽菲尔德一时语塞,无法解释了,心里很不是滋味。
于是,伽菲尔德不再散步,立即回家,潜心探讨小男孩给他出的难题。他经过反复思考与演算,终于弄清了其中的道理,并给出了简洁的证明方法。
转引自:http://tw.ntu.edu.cn/education/yanjiu/中“数学的发现”栏目。图无法转贴,请查看原文。
参考资料:http://zhidao.baidu.com/question/5159445.html1年前查看全部
- 图中的程序框图所描述的算法称为欧几里得辗转相除法.若输入m=2010,n=1541,则输出m= ___ .(注:框图中的
图中的程序框图所描述的算法称为欧几里得辗转相除法.若输入m=2010,n=1541,则输出m= ___ .(注:框图中的赋值符号“=”也可以写成“←”或“:=”)
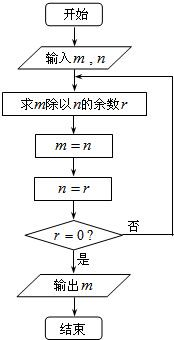
 katonge1年前1
katonge1年前1 -
 夏欲辞 共回答了17个问题
夏欲辞 共回答了17个问题 |采纳率100%解题思路:先求出m除以n的余数,然后利用辗转相除法,将n的值赋给m,将余数赋给n,进行迭代,一直算到余数为零时m的值即可.当m=2010,n=1541,m除以n的余数是469
此时m=1541,n=469,m除以n的余数是134
此时m=469,n=134,m除以n的余数是67
此时m=134,n=67,m除以n的余数是0,
此时m=67,n=0
退出程序,输出结果为67
故答案为67点评:
本题考点: ["程序框图"]
考点点评: 算法和程序框图是新课标新增的内容,在近两年的新课标地区高考都考查到了,这启示我们要给予高度重视,属于基础题.1年前查看全部
- 谁会这道题:古希腊数学家欧几里得
谁会这道题:古希腊数学家欧几里得
古希腊数学家欧几里得提出了三角形内角和等于180°的定理.到了19世纪初,俄国数学家罗巴切夫斯基提出:在凹曲面上,三角形内角之和小于180°.随后德国数学家黎曼提出:在球形凸面上,三角形内角之和大于180°.上述材料体现了 [ ] ①欧几里得定理不再是真理 ②真理有自己适用的条件和范围,真理是有条件的 ③真理是主观与客观、理论与实践的具体的历史的统一 ④不顾条件的变化,真理会转化为谬误
A、①②③
B、②③
C、②③④
D、③④ wupoo1年前1
wupoo1年前1 -
 aszxgs 共回答了20个问题
aszxgs 共回答了20个问题 |采纳率90%B1年前查看全部
- 半圆是图形还是弧?根据欧几里得所著的《几何原本》中的定义18,半圆:是直径与被它切割的圆弧围成的图形.可是我的初中老师讲
半圆是图形还是弧?
根据欧几里得所著的《几何原本》中的定义18,
半圆:是直径与被它切割的圆弧围成的图形.
可是我的初中老师讲的是半圆是弧,并非图形. adycon1年前1
adycon1年前1 -
 zhoushiling 共回答了23个问题
zhoushiling 共回答了23个问题 |采纳率91.3%图形1年前查看全部
- 欧几里得里面的“等量加或减等量仍然等于等量”是什么意思,
欧几里得里面的“等量加或减等量仍然等于等量”是什么意思,
在等式上却是如:若A=B,a=b,则A+a=B+b,但在几何上它怎么表示? 情若寒冰1年前2
情若寒冰1年前2 -
 水木森 共回答了20个问题
水木森 共回答了20个问题 |采纳率90%这个比较容易理解,我们以三维的笛卡尔直角坐标系为例(即三维直角单位坐标系,在数学上表示为R3基底的欧几里得空间).在该坐标系中,一个向量被表示为起点移动到坐标原点(欧几里得空间的0元)后终点的坐标,这个坐标就是向量坐标,即终点坐标减起点坐标.相同坐标的向量相等,也就是说,方向与长度都相同的两条平行向量是相等的.
设A的起点(x1,y1,z1)终点(x2,y2,z2),B的起点(x3,y3,z3)终点(x4,y4,z4),只要满足x2-x1=x4-x3,y2-y1=y4-y3,z2-z1=z4-z3,他们就相等,这就是前面说的方向和长度(这里用任何一种范数表示长度都不影响结论,因为任何范数下满足的一切数学定理在任意一种内积下依然满足,我们中学和本科的时候往往会用2范数,即向量的坐标平方的和开根号)都相同的向量是相等的.那么我们再找两条相等的向量与这两个向量做加法(例如A+a的坐标就是首位相接后,a的终点减A的起点).那么做完加法后,得到的两个向量A+a和B+b依然方向相同长度相等,也就是两个向量依然相等.
直观的说,就是两个方向相同且长度相等的向量,如果分别给他们加上长度相同且方向相等的向量,得到的两条新向量依然长度相同且方向相等.1年前查看全部
- 欧几里得的《几何原本》提出的 5 条公设中有 3 条为什么叫 “公设”,而不是 “定义”?
 wanghongbai1年前1
wanghongbai1年前1 -
 玲珑水阁123 共回答了23个问题
玲珑水阁123 共回答了23个问题 |采纳率95.7%公设又叫做公理,就是依据人类理性和不证自明的基本事实,经过人类长期反复实践的考验,不需要再加证明的基本命题.
注意 这是命题
比如:一条直线与两条直线都平行,则这两条直线平行 这叫公理
定义是对于一种事物的本质特征或一个概念的内涵和外延所作的确切表述
比如:角是由一个顶点和由这个顶点出发的两条射线组成的图形 这叫定义1年前查看全部
- 三角形内角之和等于180°,这是古希腊数学家欧几里得提出的定理。在此之后的两千多年里,人们一直把它当作任何条件下都适用的
三角形内角之和等于180°,这是古希腊数学家欧几里得提出的定理。在此之后的两千多年里,人们一直把它当作任何条件下都适用的真理。但是,19世纪初,俄国数学家罗巴切夫斯基提出:在凹曲面上,三角形内角之和小于180°。随后,德国数学家黎曼提出:在球形凸面上,三角形内角之和大于180度。这说明真理是 [ ]①因人而异的
②具体的
③有条件的
④客观的
A.①②
B.①③
C.①④
D.②③ 般若菠萝蜜心经1年前1
般若菠萝蜜心经1年前1 -
 syx116 共回答了16个问题
syx116 共回答了16个问题 |采纳率75%D1年前查看全部
- 三角形内角之和等于180°,这是古希腊数学家欧几里得提出的定理.在此后的两千多年里,人们一直把它当作任何条件下都适用的真
三角形内角之和等于180°,这是古希腊数学家欧几里得提出的定理.在此后的两千多年里,人们一直把它当作任何条件下都适用的真理.随着航海事业的发展和人们对于球面认识的不断深入,这一定理的局限性逐渐暴露.19世纪初,俄国数学家罗巴切夫斯基提出:在凹曲面上,三角形内角之和小于180°.随后,德国数学家黎曼提出:在球形凸面上,三角形内角之和大于180°.由此,人们关于空间的观念发生了***性的转变.这段材料说明
a.任何真理都永远是主观和客观的统一
b.任何真理都有自己的适用条件和范围
c.真理随着历史条件的变化而变化
d.真理随时随地可以转变成谬误 月儿不孤独1年前1
月儿不孤独1年前1 -
 liwiqi 共回答了18个问题
liwiqi 共回答了18个问题 |采纳率88.9%答案B
这个例题材料源自教材第47页的探究活动案例.材料说明真理是有条件的,
罗巴切夫斯基和黎曼的发现并不能否认欧几里得定理的真理性,它只证明了真理都有自己的适用条件和范围.A、D选项否认了真理的条件性,是错误的;C选项与材料无关,也不应该入选.正确答案为B.1年前查看全部
- 世界上第一个把圆周率的值精确到七位小数的数学家是. A、刘徽.B.祖冲之、C欧几里得
 风之巢1年前1
风之巢1年前1 -
 梦想空间 共回答了18个问题
梦想空间 共回答了18个问题 |采纳率94.4%选B1年前查看全部
- 欧几里得著作【 】提出了五大公设,其中有;
欧几里得著作【 】提出了五大公设,其中有;
1任何俩点可以用----------------------连接;2任何线段可以不-----------------;3给定任意线段,可以以其一个端点作为---------------------------,该线段作为------------------------作一个圆. pingtouchefu1年前3
pingtouchefu1年前3 -
 韩浪 共回答了18个问题
韩浪 共回答了18个问题 |采纳率77.8%1直线
2断延长
3圆心、半径1年前查看全部
- 欧几里得《原本》与公理化思想
 jw19825181年前1
jw19825181年前1 -
 蓝天68934 共回答了16个问题
蓝天68934 共回答了16个问题 |采纳率93.8%《原本》是古希腊数学家欧几里得(Euclid,约前330~前275)用公理建立起来的演绎体系的最早典范.在此之前,人们所积累下来的数学知识是片断的、零散的.欧几里得借助于逻辑方法,把这些知识组织起来,整理在一个比较严格的演绎体系之中.《原本》的出现对整个数学的发展产生了深远的影响,现代数学和各门科学中广泛使用的公理化方法就是从《原本》发展而来的.
《原本》共分13卷,其中第1卷首先给出23个定义、5个公设和5条公理,近代数学不分公设与公理,凡是基本假定都叫做公理.《原本》后面各卷不再列出公理.这一卷在给出的定义、公设和公理的基础上利用逻辑推理证明了48个命题.其余各卷与第1卷类似,首先给出定义,之后是命题的证明.欧几里得从119个定义、5个公设和5条公理出发,推出了465个命题.1年前查看全部
- 三角形内角之和等于180°,这是古希腊数学家欧几里得提出的定理。在此后的两千多年里,人们一直把它当作任何条件下都适用的真
三角形内角之和等于180°,这是古希腊数学家欧几里得提出的定理。在此后的两千多年里,人们一直把它当作任何条件下都适用的真理。随着航海事业的发展和人们对于球面认识的不断深入,人们发现,在凹曲面及球形凸面上,三角形的内角之和并不等于180°。这说明
A.真理向前一步就会变成谬误 B.真理是具体的、有条件的 C.真理是难以被人们认识和利用的 D.真理最基本的属性是客观性  52juli1年前1
52juli1年前1 -
 讨厌黑头 共回答了15个问题
讨厌黑头 共回答了15个问题 |采纳率73.3%B
1年前查看全部
- 《几何原本》的作者是( )A. 欧几里得B. 阿基米德C. 阿波罗尼奥斯D. 托勒玫
 sdlz12320001年前1
sdlz12320001年前1 -
 喜树部落_色彩 共回答了15个问题
喜树部落_色彩 共回答了15个问题 |采纳率93.3%解题思路:《几何原本》的作者是欧几里得即可得出.《几何原本》的作者是欧几里得.
故选:A.点评:
本题考点: 古希腊数学.
考点点评: 本题考查了数学史《几何原本》的作者,属于基础题.1年前查看全部
- 三角形内角之和等于180°,这是古希腊数学家欧几里得提出的定理。在此之后的两千多年里,人们一直把它当作任何条件下都适用的
三角形内角之和等于180°,这是古希腊数学家欧几里得提出的定理。在此之后的两千多年里,人们一直把它当作任何条件下都适用的真理。但是,19世纪初,俄国数学家罗巴切夫斯基提出:在凹曲面上,三角形内角之和小于180°。随后,德国数学家黎曼提出:在球形凸面上,三角形内角之和大于180°。这说明真理是 [ ]①因人而异的
②具体的
③有条件的
④客观的
A.①②
B.①③
C.①④
D.②③ flyinsky20051年前1
flyinsky20051年前1 -
 greatlxj 共回答了19个问题
greatlxj 共回答了19个问题 |采纳率78.9%D1年前查看全部
- 欧几里得、刘微、秦九韶、笛卡尔、费马几位数学家有什么贡献?它们有什么成长经历?
欧几里得、刘微、秦九韶、笛卡尔、费马几位数学家有什么贡献?它们有什么成长经历?
帮忙发清楚点 dugu_971年前1
dugu_971年前1 -
 刘刘123 共回答了24个问题
刘刘123 共回答了24个问题 |采纳率87.5%刘徽(生于公元250年左右)山东人,中国古代伟大的数学家.他的杰作《九章算术注》和《海岛算经》是我国最宝贵的数学遗产.刘徽是世界上最早提出十进小数概念的人,他正确地提出了正负数的概念及其加减运算的规则.提出了“割圆术”,并用“割圆术”求出圆周率π为3.14.刘徽在割园术中提出的“割之弥细,所失弥少,割之又割以至于不可割,则与园合体而无所失矣”被视为中国古代极限观念的佳作.1年前查看全部
- 三角形内角之和等于180°,这是古希腊数学家欧几里得提出的定理。在此之后的两千多年里,人们一直把它当作任何条件下都适用的
三角形内角之和等于180°,这是古希腊数学家欧几里得提出的定理。在此之后的两千多年里,人们一直把它当作任何条件下都适用的真理。但是,19世纪初,俄国数学家罗巴切夫斯基提出:在凹曲面上,三角形内角之和小于180°。随后,德国数学家黎曼提出:在球形凸面上,三角形内角之和大于180°。这说明真理是 [ ]①因人而异的 ②具体的 ③有条件的 ④客观的⑤发展的
A.①②⑤
B.①③⑤
C.①④⑤
D.②③⑤ a5236991年前1
a5236991年前1 -
 wwasdf 共回答了12个问题
wwasdf 共回答了12个问题 |采纳率83.3%D1年前查看全部
- 数学里 点 的本质理解据欧几里得的描述 点是一个不加定义的概念 还有一些性质 如不论大小 线的两端是点 .. 最经看了一
数学里 点 的本质理解
据欧几里得的描述 点是一个不加定义的概念 还有一些性质 如不论大小 线的两端是点 .. 最经看了一些数学书越来越迷惑了
1.点有没有形状?
(可能是圆吗)
(几何图形的“原子”就是点吧 就像化学中的基本粒子一样)
2.点可不可以分类?
(就像夸克也可以分为一些...)
3.线段有长度,线段是有点构成的吧?那么,长度是什么呢?
(是不是构成线段的所有点与最近相邻点之间的“线段”之和)
(线的长度是宏观的,和微观的点应该有关系吧)
4.谈论曲线的长度,有时要说什么可微不可微,什么意思?
(难道即使可以“宏观重合”的曲线 也有不同?)
弱弱的思考 望前辈指教
1.点有没有形状?
答:点没有形状,无限小. ——为什么具有这些性质呢?
2.点可不可以分类? 为什么?
答:不可分类.
3.线段有长度,线段是有点构成的吧?那么,长度是什么呢?
答:严格的说,线段不是由点构成的.是由无限小的线段构成的.点是线段的两端. ——无限小的线段不是有点构成? 古道西风清1年前3
古道西风清1年前3 -
 火中的心 共回答了17个问题
火中的心 共回答了17个问题 |采纳率94.1%1,点没大小,只是一个位置
2,不能分了
3,量变引起质变!用这个去理解
4,这个内容可以看看导数的有关理论1年前查看全部
- 用扩展欧几里得(Euclid)算法计算1234 mod 4321的乘法逆元
用扩展欧几里得(Euclid)算法计算1234 mod 4321的乘法逆元
如题,这使我密码学的一道题,不需要编程,求高手把它当数学题给我把计算过程写出来,给我那张表即可.我会算当f>d时,f mod d 的乘法逆元,但是当f小于d时我就不会算了.请高手把那张Q,X1,X2,X3,Y1,Y2,Y3的计算表发给我,
注:答案应该为3239
不用答了,我已经算出来了 beijinglang1年前3
beijinglang1年前3 -
 rannuo 共回答了20个问题
rannuo 共回答了20个问题 |采纳率85%Q X1 X2 X3 Y1 Y2 Y3
1 0 4321 0 1 1234
3 0 1 1234 1 -3 619
1 1 -3 619 -1 4 615
1 -1 4 615 2 -7 4
153 2 -7 4 -307 1075 3
1 -307 1075 2 309 -1082 1
4321-1082=32391年前查看全部
- (2014•云南一模)如图所示的程序框图描述的算法称为欧几里得辗转相除法,若输入m=2010,n=1541,则输出的m的
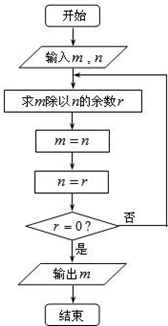 (2014•云南一模)如图所示的程序框图描述的算法称为欧几里得辗转相除法,若输入m=2010,n=1541,则输出的m的值为( )
(2014•云南一模)如图所示的程序框图描述的算法称为欧几里得辗转相除法,若输入m=2010,n=1541,则输出的m的值为( )
A.2010
B.1541
C.134
D.67 changxia0101年前1
changxia0101年前1 -
 yhhuhhhh 共回答了14个问题
yhhuhhhh 共回答了14个问题 |采纳率92.9%解题思路:程序的运行功能是求m=2010,n=1541的最大公约数,根据辗转相除法可得m的值.由程序框图知:程序的运行功能是求m=2010,n=1541的最大公约数,
∵2010=1541+469;
1541=3×469+134;
469=3×134+67;
134=2×67+0;
∴此时m=67.∴输出m的值为67.
故选:D.点评:
本题考点: 程序框图.
考点点评: 本题考查了辗转相除法的程序框图,掌握辗转相除法的操作流程是关键.1年前查看全部
- 1、浮力定律是谁提出的:() (2.0分) A.欧几里得 B.亚里士多德 C.阿基米德 D.苏格拉底 2、公元前三百多年
 lhq_00001年前4
lhq_00001年前4 -
 or2q 共回答了18个问题
or2q 共回答了18个问题 |采纳率94.4%C.阿基米德1年前查看全部
- 欧几里得的名言“在几何里,没有专为国王铺设的大道”的英文是什么?
 rubishzd1年前2
rubishzd1年前2 -
 big_wei 共回答了17个问题
big_wei 共回答了17个问题 |采纳率94.1%There was no royal road to geometry.
原文是
Ptolemy I,king of Egypt,asked Euclid "if there was in geometry any shorter way than that of the Elements",and he answered that there was no royal road to geometry.1年前查看全部
- 欧几里得讲的全是几何问题?和我们平时学的高等数学,线性代数,概率论有关系吗?
欧几里得讲的全是几何问题?和我们平时学的高等数学,线性代数,概率论有关系吗?
欧几里得讲的全是几何问题?
和我们平时学的高等数学,线性代数,概率论有关系吗?
能用深入潜出的话解释下吗? 晨曦玫瑰1年前4
晨曦玫瑰1年前4 -
 belmontj 共回答了16个问题
belmontj 共回答了16个问题 |采纳率93.8%欧式几何就是普通意义上的几何.
欧式几何跟非欧几何最大的差别在于,
欧式几何是建立在平面假设上的几何,非欧几何是建立在球面假设上的几何.
比如,欧式几何认为,平行线间没有交点,非欧几何认为,平行线间有一个交点,这个交点在无穷远处.
其实,我们学习的高数,从思维方法上,更接近于非欧几何.而线代更接近于欧式几何.
概率论?
这个好像没什么关系.1年前查看全部
- 1、浮力定律是谁提出的:() (2.0分) A.欧几里得 B.亚里士多德 C.阿基米德 D.苏格拉底 2、公元前三百多年
 bentseng1年前2
bentseng1年前2 -
 FL泪流手心 共回答了20个问题
FL泪流手心 共回答了20个问题 |采纳率90%C1年前查看全部
- 阿基米德和欧几里得的国籍都在一个时代吗?
 warren19301年前1
warren19301年前1 -
 yayazhu 共回答了21个问题
yayazhu 共回答了21个问题 |采纳率95.2%阿基米德(Archimedes)
生卒年代:前287-212
古希腊伟大的数学家、力学家.
欧几里德(Euclid of Alexandria),希腊数学家.约生于公元前330年,约殁于公元前260年.
欧几里德是古代希腊最负盛名、最有影响的数学家之一,他是亚历山大里亚学派的成员.1年前查看全部
- 古希腊数学家欧几里得的著作<<几何原本>>是从哪个世纪初开始传入我国的?
 枫叶荻1年前1
枫叶荻1年前1 -
 sxcsfbhjhy 共回答了21个问题
sxcsfbhjhy 共回答了21个问题 |采纳率90.5%16世纪,意大利人利玛窦.
1582年,意大利人利玛窦到我国传教,带来了15卷本的《原本》.
1600年,明代数学家徐光启(1562- 1633)与利玛窦相识后,便经常来往.
1607年,他们把该书的前6卷平面几何部分合译成中文,并改名为《几何原本》.
后9卷是1857年由我国清代数学家李善兰(1811-1882)和英国人伟烈亚历译完的.1年前查看全部
大家在问
- 1已知,a的平方加3a加1等于0,求(1)a+1/a的值,(2)a的平方加a的平方分之1的值
- 2“3.8V,0.3A”“1.5V,0.3A”如何区分两个灯泡
- 3英语小作文,大家帮我指出其中的错误哈!有很多错误啊!
- 4求连接1+i与1-4i的直线段的参数方程
- 5用过去分词重写下列句子.nine out of ten women who were interviewed about
- 6如果你能安静下来,全世界都会为你沉寂
- 7高中生物题(关于限制性内切酶)目前已经发现了200多种限制性内切酶,这些酶都有特异性,分别只能识别特定的脱氧核苷酸序列,
- 8一根10米长的木棍,从一段开始逐次锯成2米一段的小木棍,锯一次用时3分钟,然后休息1分钟,全部锯完要
- 9.一根10米长的木棍,从一段开始逐次锯成2米一段的小木棍,锯一次用时3分钟,然后休息1分钟,全部锯完
- 10怎么翻译始终以质量求生存、以科技求进步、以服务求市场
- 11哪些有机物可溶于水(高中认识的有机物)
- 12氧化铁中铁指原子分子还是元素
- 134氧化3铁中铁原子与氧原子各显几价?
- 14怎样鉴别稀硫酸、浓盐酸、氯化铁溶液、硫酸铜溶液.
- 15火星离太阳多远?